Что такое область существования

Область существования функции

Область существования функции

Пример 2. Поскольку корень квадратный из отрицательного числа является комплексным числом, отрицательное число не попадает в область существования и не обрабатывает комплексные числа.

Область существования функции y = Y

x состоит из всех неотрицательных чисел. Людмила Фирмаль

\ gx имеет область существования, состоящую из всех положительных чисел, т.е. x> 0. Пример 4. y = • Это область существования Функции — все действительные числа.

Кроме —1 и + 1 — Числа −1 и +1 не классифицируются как существующие, поскольку знаменатель исчезает при этих значениях и не может быть разделен на ноль. ^

Пример 5 Все положительные числа, кроме 1. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Область определения функции

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

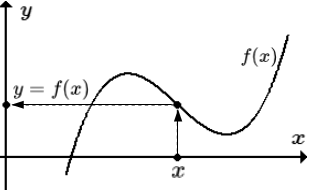
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.

Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:

Например, все действительные числа от 2 до 5 включительно можно записать так:

Все положительные числа можно описать так:

Ноль не положительное число, поэтому скобка возле него круглая.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.

Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.

Область определения функции с корнем

Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).

Пример

Найти область определения функции:

Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.

Разложим квадратный трёхчлен на множители:

Дискриминант положительный. Ищем корни:

Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).

Область определения степенной функции

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

Рассмотрим несколько примеров.

Область определения показательной функции

Область определения показательной функции — это множество R.

Примеры показательных функций:

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

Рассмотрим примеры логарифмических функций:

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Составим и решим систему:

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.

Функция

Область определения функции

Источник

область существования

Смотреть что такое «область существования» в других словарях:

Область (местность) — Область (от старослав. облада ‒ владение), местность, земля, край; часть какой либо территории (страны, государства, материка, земной суши и т.п.), выделяемая при районировании по определённому существенному признаку (природным условиям,… … Большая советская энциклопедия

Область — I Область (от старослав. облада владение) местность, земля, Край; часть какой либо территории (страны, государства, материка, земной суши и т.п.), выделяемая при районировании по определённому существенному признаку (природным условиям,… … Большая советская энциклопедия

СМИРНОВА ОБЛАСТЬ — область типа С, область типа S, ограниченная односвязная область Gс жордановой спрямляемой границей на комплексной плоскости со свойством: существует такое однолистное конформное отображение круга | w| Математическая энциклопедия

Волынь историческая область — область, получившая название от города Волынь или Велынь (см.). В древности была населена славянскими племенами: дулебами (которые стали потом называться бужанами и в середине IX в. волынянами), затем древлянами и дреговичами, жившими на северо… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Волынь, историческая область — область, получившая название от города Волынь или Велынь (см.). В древности была населена славянскими племенами: дулебами (которые стали потом называться бужанами и в середине IX в. волынянами), затем древлянами и дреговичами, жившими на северо… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Киевская область (ВСЮР) — У этого термина существуют и другие значения, см. Киевская область (значения). Киевская область ВСЮР Флаг … Википедия

Бисерово (Кировская область) — Село Бисерово Страна РоссияРоссия … Википедия

Глубокское гетто (Витебская область) — Глубокское гетто Местонахождение Глубокое Координаты … Википедия

Усатово (Саратовская область) — У этого термина существуют и другие значения, см. Усатово. Село Усатово Страна РоссияРоссия … Википедия

Центрально-Чернозёмная область — Центрально Чернозёмная область административно территориальная единица РСФСР 1928 … Википедия

Нижнеамурская область — Страна … Википедия

Источник

Определение функции

Определение функции

Сложные функции

Действительные функции

В математическом анализе большую роль играют числовые функции.

Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.

Максимум и минимум

Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.

Верхняя и нижняя грани

Монотонные функции

Многозначные функции

Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.

Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.

Сужение и продолжение функции

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Область существования и область значения функции

Определение.Областью существования (или областью определения) функции y=f(x) называется совокупность всех действительных значений аргумента х, для которых функция у определена, то есть существует и выражается действительным числом.

Совокупность всех значений, которые принимает при этом сама функция у, называется областью значений (или областью изменения) этой функции.

Упражнения. Найти область определения функции:

1) у= ;

2) ;

3) у=lg(x − 5x+6).

Четность и нечетность.

Определение.Функция у=f(x) называется четной, если для любых значений х из области определения выполняется равенство: f(−x) = f(x).

График четной функции симметричен относительно оси ординат (рис. 9).

Определение.Функция у=f(x) называется нечетной, если для любых значений х из области определения выполняется равенство: f(−x)=−f(x).

График нечетной функции симметричен относительно начала координат (рис. 10).

Если ни одно из вышеуказанных условий не выполняется (т.е f(−x)¹−f(x) и f(−x)¹f(x)), то функция y = f(x) называется функцией общего вида.

Функция у=х − нечетная; у=х +х −5 – произвольного вида (показать это самостоятельно).

2.4. Периодичность.

Определение.Функция у=f(x) называется периодической с периодом Т¹0, если для любых х из области определения справедливо равенство:

Замечание. Если число Т есть период функции у=f(x), заданной на всей числовой прямой, то число nT, где n Î Z, также является периодом функции. В этом случае наименьший положительный период, если он существует, называется основным периодом функции. Говоря о периоде функции, обычно имеют в виду наименьший положительный период.

Монотонность.

Определение.Функция у=f(x) называется возрастающей на некотором интервале, если на этом интервале большему значению аргумента соответствует большее значение функции, т.е. при х₁ x f(x )>f(x )]

Определение.Функция у=f(x) называется убывающей на некотором интервале, если на этом интервале большему значению аргумента соответствует меньшее значение функции, т.е. при х f(x ),т.е.

(«x , x ÎDf) [x >x f(x ) 0 и монотонно убывающей при k 1 и монотонно убывающей, когда а 0, что

В противном случае функция называется неограниченной.

Если функция ограничена на некотором промежутке, то график ее в пределах этого интервала расположен в полосе, ограниченной прямыми у=а и у=b (рис. 13).

Пример.Функция у= sin x ограничена на всей числовой оси, т.к.

Источник