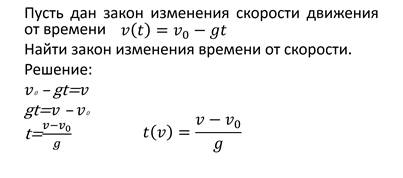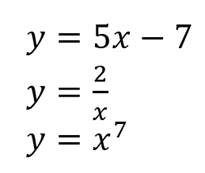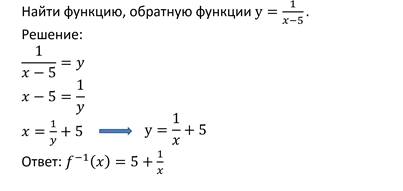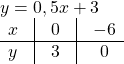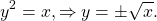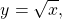Что такое обратимая функция приведите пример

Обратная функция

Урок 3. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Обратная функция»

· познакомиться с понятиями прямой и обратной функции;

· познакомиться с понятием обратимой функции;

· научиться находить обратные функции;

· рассмотреть свойство обратных функций.

Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Рассмотрим ещё одну задачу.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.

Давайте рассмотрим с вами ещё одну задачу.

Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.

Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.

Приведём примеры обратимых функций:

Давайте разберём это определение на примере.

Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.

Сформулируем основные свойства обратных функций.

Источник

Обратимые и обратные функции

Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.

Примеры обратимых функций:

Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.

Примеры обратных функций:

Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:

Графики функций будут симметричны относительно прямой y=x:

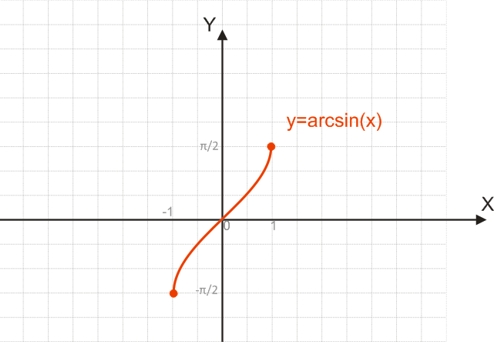
Функция y=arcsin(x)

Поскольку функция y=sin(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.

График функции y=arcsin(x):

Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.

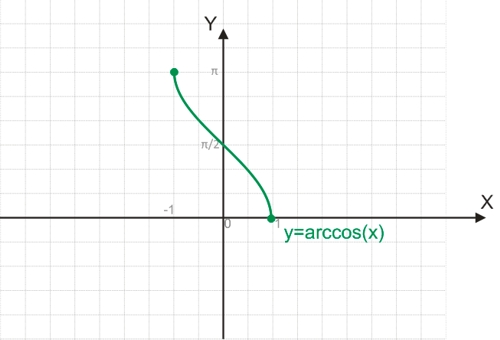
Функция y=arccos(x)

Поскольку функция y=cos(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.

График функции y=arccos(x):

Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.

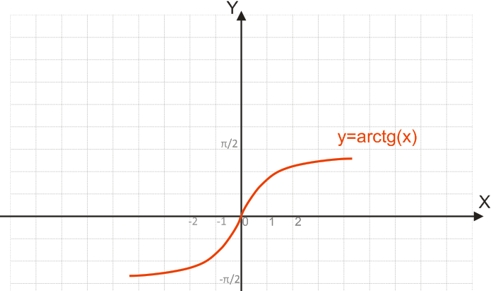
Функция y=arctg(x)

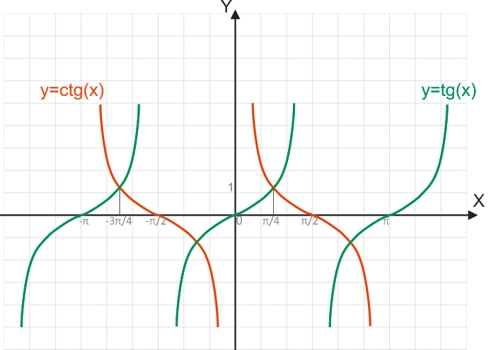
Поскольку функция y=tg(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.

График функции y=arctg(x):

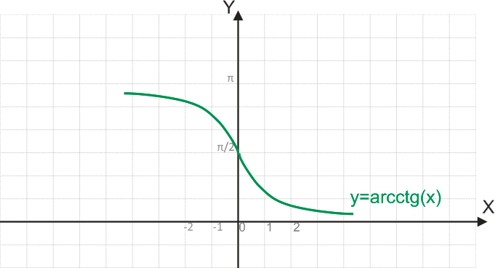
Функция y=arcctg(x)

Поскольку функция y=ctg(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.

График функции y=arcctg(x):

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

«ОБРАТИМАЯ И ОБРАТНАЯ ФУНКЦИЯ»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

ввести понятия обратимой и обратной функции;

провести доказательство теоремы о монотонности прямой и обратной функции;

выявить и обосновать геометрический смысл обратимости функции;

формировать умение находить обратную функцию для заданной.

1. Дана функция

а) Исследуйте функцию на монотонность, если х  2.

б) Найдите наибольшее и наименьшее значения функции на отрезке [–1,5; 1,5].

2. Исследуйте функцию где х > 0, на ограниченность.

3. Исследуйте функцию на четность.

1. Дана функция

а) Исследуйте функцию на монотонность, если х  2.

б) Найдите наибольшее и наименьшее значения функции на отрезке [–4,5; –3,1].

2. Исследуйте функцию где х

3. Исследуйте функцию на четность.

1. Дана функция

а) Исследуйте функцию на монотонность, если х  –1.

б) Найдите наибольшее и наименьшее значения функции на отрезке [–2; 0,4].

2. Исследуйте функцию где х

3. Исследуйте функцию на четность.

1. Дана функция

а) Исследуйте функцию на монотонность, если х  1.

б) Найдите наибольшее и наименьшее значения функции на отрезке [0; 2,2].

2. Исследуйте функцию где х > 2, на ограниченность.

3. Исследуйте функцию на четность.

Решение некоторых вариантов проверочной работы.

В зависимости от уровня подготовки класса учитель вправе дать учащимся не всю работу, а выборочные задания. Варианты 1 и 2 несколько легче вариантов 3 и 4.

1. Обозначим

а) Пусть тогда

функция убывает на (–  ; 2].

б) Так как функция убывает на (–  ; 2], то

Ответ : а) убывает; б) у _наиб. = 12,25; у _наим. = 0,25.

2. где х > 0.

Функция ограничена сверху прямой у = 0, значит, функция ограничена сверху прямой у = 1.

Ответ : ограничена сверху.

3. – симметрична относительно начала координат. значит, функция нечетная.

1. а) Обозначим Графиком является парабола с вершиной в точке (–1; –1) и пересекающая ось 0 х в точках х = 0 и х = –2.

Если х  –1, то функция возрастает.

б) На отрезке [–2; 0,4]

и

Ответ : а) возрастает; б) у _наиб. = 0,96; у _наим. = 0.

2. где х

Функция ограничена снизу прямой у = 0, значит, функция ограничена снизу прямой у = 2.

Ответ : ограничена снизу.

3. – симметрична относительно начала координат.

Если х  0, то

Имеем: значит, функция ни четная, ни нечетная.

Ответ : ни четная, ни нечетная.

3. Объяснение нового материала.

1. Для введения понятия обратимой функции можно использовать либо подвижные модели, либо изображение обратимых и необратимых функций на прозрачной пленке, перевернув которую можно показать, как область определения и область значения функции «меняются местами» и в каком случае обеспечивается однозначность обратной функции.

2. Для первичного закрепления материала учащиеся выполняют следующее задание.

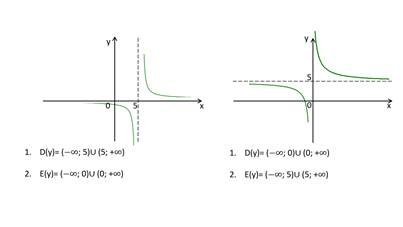
Среди функций, графики которых изображены на рисунке, укажите обратимые.

Подчеркиваем учащимся, что в теореме сформулирован признак обратимости функции (достаточное условие). В то же время монотонность не является необходимым условием обратимости.

4. Устанавливая геометрический смысл обратимости функции, учащиеся формулируют способ построения графика обратной функции с помощью преобразования осевой симметрии.

4. Формирование умений и навыков.

Упражнения, решаемые на этом уроке, направлены на аналитическое задание функции, обратной данной, а также на построение графика обратной функции с помощью осевой симметрии.

1. № 3.1 (а; б), № 3. 2 (а; б).

При выполнении этих упражнений следует предупредить формализм в аналитическом задании функции путем простого преобразования уравнения. Учащиеся должны обосновать существование обратной функции.

Ответ :

Функция убывает на всей области определения, значит, существует обратная функция, определенная и убывающая на

Ответ :

2. № 3.3 (а; б), № 3. 4 (а; б), № 3.5* (а; б).

Графиком является кубическая парабола, полученная из графика у = х 3 сдвигом вправо по оси 0 х на 2 единицы.

Ответ :

– Какая функция называется обратимой?

– Сформулируйте признак обратимости функции.

– Дайте определение обратной функции.

– Каков характер монотонности прямой и обратной функций?

– Как построить график обратной функции, используя график данной функции?

Домашнее задание: № 3.1 (в; г) – № 3.4 (в; г), № 3.5 * (в; г).

Источник

Взаимно обратные функции, основные определения, свойства, графики

Понятие обратной функции

Для чего вообще нам нужно понятие обратных функций?

Нахождение взаимно обратных функций

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным.

Решение

Обе взаимно обратные функции можно отобразить на графике следующим образом:

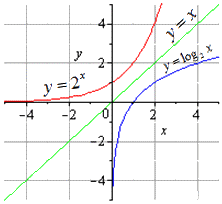
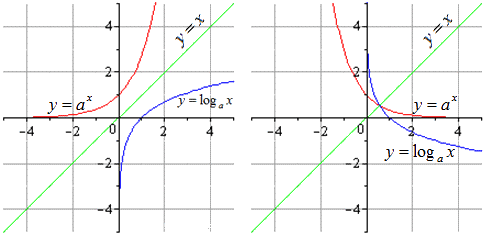
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Решение

В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

На графике обе функции будут выглядеть так:

Основные свойства взаимно обратных функций

a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3

Графики взаимно обратных функций

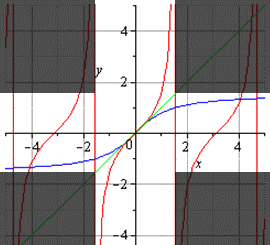
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

Графики для функций с a > 1 и a 1 будут выглядеть так:

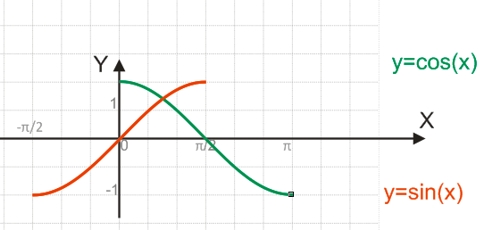
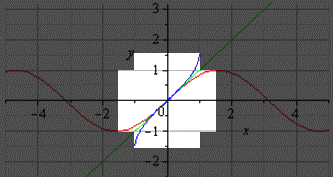
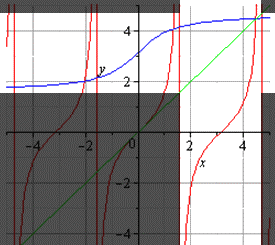
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

График главной ветви косинуса и арккосинуса выглядит так:

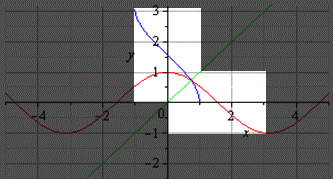
График главной ветви арктангенса и тангенса:

График главной ветви арккотангенса и котангенса будет таким:

Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Источник

Обратная функция

Что такое обратная функция? Как найти функцию, обратную данной?

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо :

1) В формулу функции вместо y подставить x, вместо x — y:

2) Из полученного равенства выразить y через x:

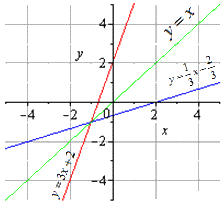
Найти функцию, обратную функции y=2x-6.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).

Теорема (необходимое и достаточное условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

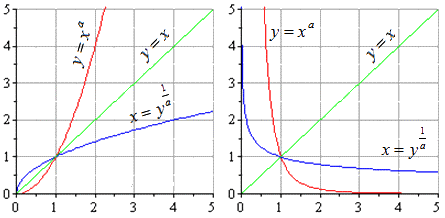
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

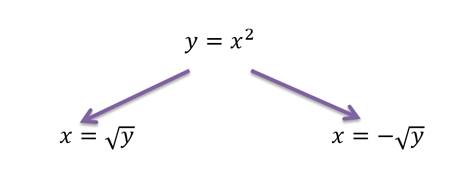
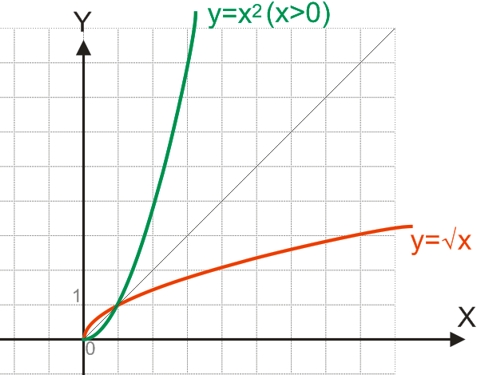
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.

Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).

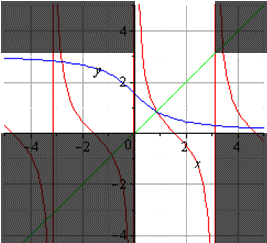
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:

В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.

1 комментарий

Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?

Источник