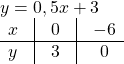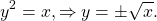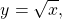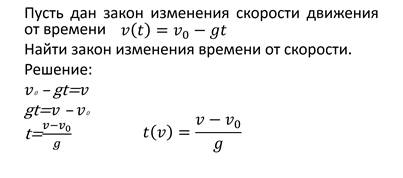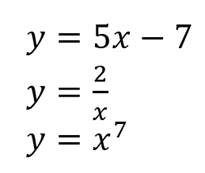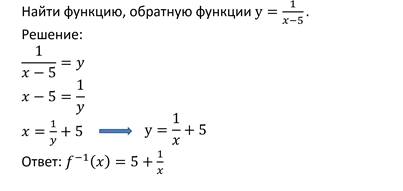Что такое обратная функция
Взаимно обратные функции, основные определения, свойства, графики
Понятие обратной функции
Для чего вообще нам нужно понятие обратных функций?
Нахождение взаимно обратных функций
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Решение
Обе взаимно обратные функции можно отобразить на графике следующим образом:
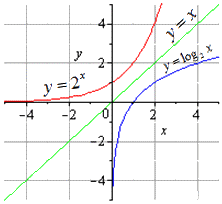
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Решение
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3
Графики взаимно обратных функций
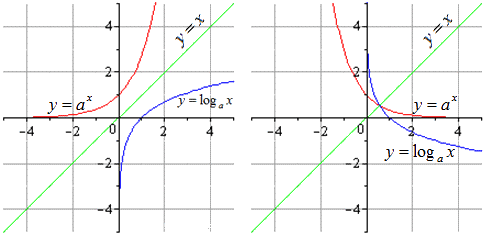
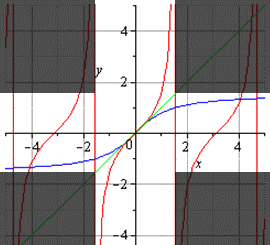
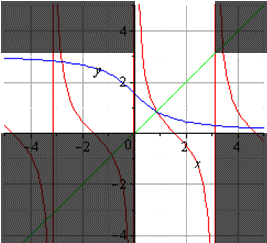
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
Графики для функций с a > 1 и a 1 будут выглядеть так:
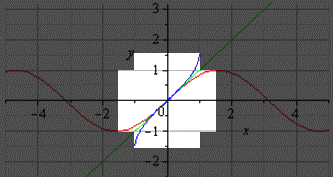
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
График главной ветви косинуса и арккосинуса выглядит так:
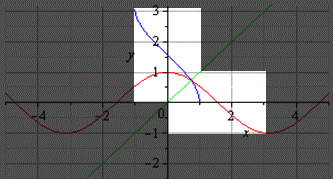
График главной ветви арктангенса и тангенса:
График главной ветви арккотангенса и котангенса будет таким:
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
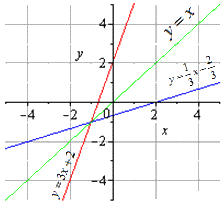
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
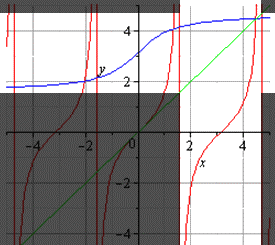
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
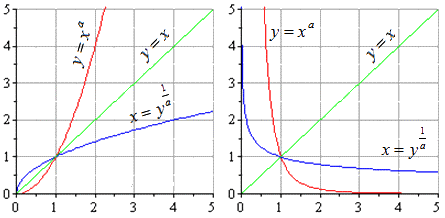
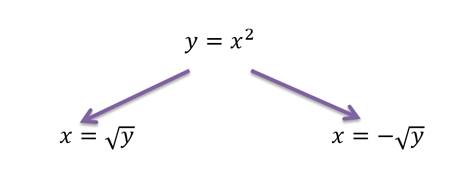
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
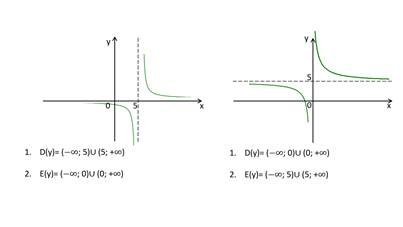
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?
Обратная функция
Урок 3. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Обратная функция»
· познакомиться с понятиями прямой и обратной функции;
· познакомиться с понятием обратимой функции;
· научиться находить обратные функции;
· рассмотреть свойство обратных функций.
Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Рассмотрим ещё одну задачу.
Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.
Давайте рассмотрим с вами ещё одну задачу.
Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.
Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.
Приведём примеры обратимых функций:
Давайте разберём это определение на примере.
Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.
Сформулируем основные свойства обратных функций.
Обратная функция
Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x.
Еще один пример взаимно-обратных функций:
Вспомним определение функции. Числовая функция y = f(x) — это такое соответствие между двумя числовыми множествами A и B, при котором каждому числу x ∈ A отвечает одно-единственное число y ∈ B. Множество A называется при этом областью определения функции, множество B — областью значений.
Пусть соответствие f является взаимно-однозначным:
Тогда существует функция g, которая действует в обратную сторону: каждому числу y ∈ B она ставит в соответствие одно-единственное число x ∈ A, такое, что f(x) = y:
Функция g называется обратной к функции f. Точно так же и функция f будет обратной к функции g.
Если мы возьмём какое-либо число x ∈ A и подействуем на него функцией f, то получим число y = f(x) ∈ B. Теперь на полученное число y подействуем функцией g. Куда попадём? Правильно, вернёмся к исходному числу x. Это можно записать так:
 | (1) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число 3 в степень x, а затем совершить обратное действие — взять от полученного числа 3 x логарифм по основанию 3 — мы вернёмся к исходному числу x:
Графики взаимно-обратных функций симметричны относительно прямой у = x.
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
1) Выражаем из формулы функции x через у. Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Обратная функция
Урок 3. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Обратная функция»
· познакомиться с понятиями прямой и обратной функции;
· познакомиться с понятием обратимой функции;
· научиться находить обратные функции;
· рассмотреть свойство обратных функций.
Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Рассмотрим ещё одну задачу.
Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.
Давайте рассмотрим с вами ещё одну задачу.
Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.
Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.
Приведём примеры обратимых функций:
Давайте разберём это определение на примере.
Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.
Сформулируем основные свойства обратных функций.