Что такое обратная теорема в геометрии
Обратная теорема
Полезное
Смотреть что такое «Обратная теорема» в других словарях:
ОБРАТНАЯ ТЕОРЕМА — теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие … Большой Энциклопедический словарь
обратная теорема — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN converse theorem … Справочник технического переводчика
обратная теорема — теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие. * * * ОБРАТНАЯ ТЕОРЕМА ОБРАТНАЯ ТЕОРЕМА, теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие … Энциклопедический словарь
ОБРАТНАЯ ТЕОРЕМА — теорема, условием к рой служит заключение теоремы исходной (прямой), а заключением условие. Обратной к О. т. будет исходная (прямая) теорема, так что прямая и О. т. взаимно обратны. О. т. равносильна теореме, противоположной к прямой, т. е.… … Математическая энциклопедия
ОБРАТНАЯ ТЕОРЕМА — теорема, условием к рой служит заключение исходной (прямой) теоремы, а заключением условие … Естествознание. Энциклопедический словарь
Теорема Фалеса — Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему. Теорема Фалеса одна из теорем планиметрии. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести… … Википедия
Теорема — (греч. theorema, от theoréo рассматриваю, исследую) предложение некоторой дедуктивной теории (см. Дедукция), устанавливаемое при помощи Доказательства. Каждая дедуктивная теория (математика, многие её разделы, логика, теоретическая… … Большая советская энциклопедия
Теорема Пифагора — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 … Википедия
ОБРАТНАЯ СВЯЗЬ — воздействие результатов к. л. процесса на его протекание. Если при этом интенсивность процесса возрастает, то О. с. наз. п о л о ж и т е л ь н о й, а в противопол. случае о т р и ц а т е л ь н о й. Отрицат. О. с. может обеспечить автоматич.… … Физическая энциклопедия
обратная предельная теорема — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN converse limit theorem … Справочник технического переводчика
Презентация по геометрии по теме «Теорема, обратная данной»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Теорема, обратная данной
Теорема – это утверждение, справедливость которого устанавливается путем рассуждений, т.е. доказательством.
Теорема Условие Заключение
У З Теорема: У З Теорема, обратная данной
Теоремой, обратной данной называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
Теорема: Если два угла смежные, то их сумма = 180°. Теорема, обратная данной: Если сумма двух углов = 180°, то эти углы смежные.
Теорема, обратная данной: Если сумма двух углов = 180°, то эти углы смежные. В А О С а b 1 2
Теорема: Если треугольник равнобедренный, то углы при основании равны. Теорема, обратная данной: Если углы треугольника при основании равны, то этот треугольник равнобедренный.
А В С Теорема, обратная данной: Если углы треугольника при основании равны, то этот треугольник равнобедренный.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Теорема, обратная данной: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Теорема, обратная данной: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Если при пересечении двух прямых секущей сумма односторонних углов = 180°, то прямые параллельны. Теорема, обратная данной: Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.
Задача №1: А С В М N
Задача №2: А В D E С 3 1 2
Задача №3: А В D E С
Задача №4: А С В D E
Задача №5: А С В D O
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: 5325021255
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В Петербурге школьникам разрешили уйти на каникулы с 25 декабря
Время чтения: 2 минуты
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
В Хабаровском крае введут уроки по вакцинации в некоторых школах и колледжах
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Костромская область разработала программу привлечения педагогических кадров
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Что такое обратная теорема в геометрии
ТЕМА УРОКА: Обратная теорема
Обратная теорема, теорема, условием которой служит заключение исходной теоремы, а заключением — условие. Обратной к Обратная теорема будет исходная теорема. Таким образом, Обратные теоремы взаимно обратны. Например, теоремы: «если два угла треугольника равны, то их биссектрисы равны» и «если две биссектрисы треугольника равны, то соответствующие им углы равны» — являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: «если число делится на 6, то оно делится на 3» — верна, а Обратная теорема: «если число делится на 3, то оно делится на 6» — неверна. Даже если Обратная теорема верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема «две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются», так и обратная к ней теорема «две непересекающиеся прямые на плоскости имеют общий перпендикуляр». Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. Обратная теорема равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный способ «доказательства от противного» как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения.
Что же такое необходимое и достаточное условие.
Необходимые и достаточные условия. Необходимыми условиями правильности утверждения называются такие условия, без соблюдения которых утверждение заведомо не может быть верным, а достаточными условиями правильности утверждения называются условия, при выполнении которых утверждение заведомо верно. Например, необходимым условием делимости целого числа на 2 является то, чтобы число, будучи записано в десятичной системе счисления, не кончалось цифрой 7. Условие это необходимо, но не достаточно, так как, например, число 23 не кончается цифрой 7 и всё-таки не делится на 2. Достаточным условием делимости числа на 2 является то, чтобы оно кончалось цифрой 0. Это условие достаточно, но не необходимо, так как число 38 не кончается цифрой 0 и все-таки делится на 2. Обычно употребляемый признак делимости на 2 (чтобы число делилось на 2, необходимо и достаточно, чтобы последняя его цифра делилась на 2) является примером условия одновременно необходимого и достаточного. Часто выражение «необходимо и достаточно» заменяется выражением «тогда и только тогда» или же выражением «в том и только в том случае».
Необходимые и достаточные условия обладают наибольшей познавательной ценностью. В сложных математических проблемах разыскание удобных для пользования необходимые и достаточные условия бывает иногда чрезвычайно трудным. В таких случаях достаточные условия стараются сделать, возможно, более широкими, т. е. охватывающими возможно большее число случаев, в которых интересующий нас факт всё ещё имеет место, а необходимые условия — возможно более узкими, т. е. охватывающими возможно меньше лишних случаев, в которых изучаемый факт уже не имеет места. Таким образом, достаточные условия постепенно сближаются с необходимыми.
Теперь немного подробней рассмотрим Лобачевского геометрию, о какой мы вспоминали выше.
Лобачевского геометрия, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Лобачевского геометрия вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Лобачевского геометрия имеет вполне реальный смысл.
Рассмотрим реальный примет обратной теоремы с доказательством.
Файл:T.gif Теорема о трех перпендикулярах.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
Файл:T.gif Обратная теореме о трех перпендикулярах.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.
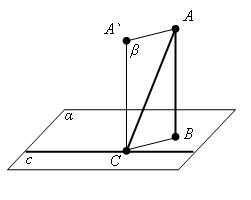
Пусть АВ – перпендикуляр к плоскости «a», АС – наклонная и «с» – прямая в плоскости «a», проходящая через основание наклонной СK. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости «a» (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой «с». Проведем через параллельные прямые АВ и СК плоскость «b» (параллельные прямые определяют плоскость, причем только одну). Прямая «с» перпендикулярна двум прямым лежащим в плоскости «b», это АС по условию и СК по построению, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами проекция ВС перпендикулярна прямой «с», лежащей в плоскости «a».
Еще один вид интерпретации данной теоремы:
Файл:T.gif Теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной CA, то она, будучи перпендикулярна и прямой CA`, перпендикулярна плоскости β, а значит, и проекции наклонной BC. Теорема доказана.
Определения, изложенные в «Началах» Евклида, не удовлетворяют тре-бованиям современной науки. Вот некоторые из 23 определений, которыми на-чинается первая книга «Начал».
Такие определения нельзя считать логически конкретными.
Во-первых, в этих определениях употребляются такие понятия (часть, длина, ширина, грани-ца и т.д.), которые сами должны быть определены. Во-вторых, идея основных понятий (в современном смысле) у Евклида вообще отсутствует.
В-третьих, не-которые его определения туманны и непонятны, например, 4 и 7. Вообще же определения Евклида являются лишь описанием геометрических образов, и, как правило, для доказательства теорем он ими не пользовался.
Список использованных источников:
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Что такое аксиома, теорема и доказательство теоремы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.