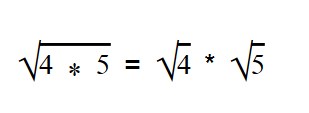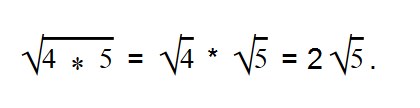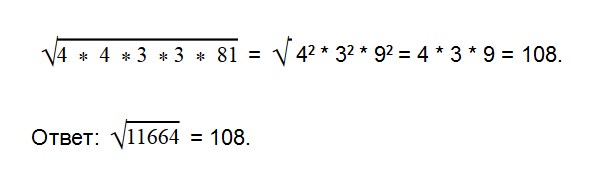Что такое общий корень

Однокоренные слова

2 класс, 3 класс, 5 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое однокоренные слова в русском языке

Однокоренные слова — это слова разных частей речи, которые объединяет смысловой корень. Однокоренные слова также могут относиться к одной части речи, тогда у них будут разные приставки и суффиксы.

Проще говоря, однокоренными являются близкие по смыслу слова с одним и тем же корнем.

Однокоренные слова так называются, потому что в их морфемном составе есть одна главная часть, которая содержит общее значение — корень.

К примеру, прилагательным «смелый» называют храброго человека, который не боится трудностей и опасностей. Лексическое значение этого слова заключается в корне смел-, который видно в морфемном составе близких по смыслу слов:

Теперь мы знаем, какие слова являются однокоренными. По-другому эти слова еще называются родственными.

Как образуются однокоренные слова

Как мы уже говорили, однокоренные слова образуются при помощи приставок и суффиксов. Процесс образования однокоренных слов называют словообразованием. Приставки и суффиксы дают слову определенный оттенок. Например, слоненок — это не то же, что слон, это его детеныш.

Во 2 классе школьники знакомятся с однокоренными словами и закрепляют знания на протяжение всего времени обучения. Давайте научимся различать однокоренные (родственные) слова от грамматических форм одного слова.

Изучайте русский язык в онлайн-школе Skysmart — с внимательными преподавателями и на интересных примерах из современных текстов.

Какие слова не являются однокоренными

Слова с омонимичными корнями

В русском языке есть такое понятие, как омонимичные корни — когда у одинаковых на вид корней разный лексический смысл. Чтобы понять, являются слова родственными или у них просто похожие корни, нужно знать их значения. Если не уверены в значениях — загляните в толковый словарь.

Красавица — красивый, красота, красивенький, покрасоваться, красавчик.

Лексическое значение корня -крас-: привлекательный, приятный вид, впечатляющий.

Краска — красить, подкрасить, перекрасить, краситель, раскраска.

Корень -крас- здесь имеет значение придания чему-либо цвета.

В каждом ряду мы видим родственные однокоренные слова. Но вот слова краситель и красивый не являются однокоренными — просто они имеют омонимичные корни.

Еще примеры неродственных слов с омонимичными корнями:

Любовь — любитель, любимый, любить.

Бурить — бурильщик, буровая, бур.

Буря — бурный, буревестник.

Формы одного слова

Однокоренные слова следует отличать от форм одного и того же слова. Для этого нужно понимать, какие морфемы являются словообразующими, а какие — формообразующими.

Словообразующие морфемы предназначены для образования новых слов. К ним относятся:

Формообразующие морфемы образовывают формы одного и того же слова. К ним относятся:

суффикс прошедшего времени глагола -л-;

суффикс повелительного наклонения глагола -и-.

Примеры форм одного и того же слова:

Лес — леса, лесу, лесом — окончание образует форму числа и падежа существительного.

Соберу — собрал — суффикс образует форму прошедшего времени глагола.

Слова в одном ряду не являются однокоренными — это формы одного и того же слова. К формам слова всегда относятся слова одной части речи, в то время как однокоренные слова могут принадлежать к разным частям речи.

Зачем подбирать однокоренные слова

Подбирать однокоренные слова — полезный навык, чтобы грамотно писать. Например, можно проверить, какая гласная пишется в безударной позиции в корне, если подобрать родственное слово, где эта гласная будет под ударением. Также через подбор однокоренных слов можно проверить написание согласных в корне.

Проверяемая гласная в корне:

обижа́ть — оби́да;

чистота́ — чи́сто;

хо́лод — холо́дный.

Правописание звонких и глухих согласных в корне:

книжка — книжечка;

дуб — дубовый;

гибкость — гибок.

Правописание непроизносимых согласных в корне:

солнце — солнечный;

грустный — грусть;

сердце — сердечный.

Источник

Родственные и однокоренные слова: в чем отличие?

Подбирать родственные слова для проверки орфограмм детей учат, начиная с первого класса. Тем не менее, даже некоторые старшеклассники затрудняются с выполнением этого задания. Более того – нередко, взрослые, помогая своим детям с домашним заданием по русскому языку, испытывают трудности. Их сбивают с толку такие определения, как «родственные» и «однокоренные» слова. Многие подзабыли, чем они отличаются друг от друга.

Формулировки в современных учебниках довольно расплывчаты и не всегда могут прояснить ситуацию. Попробуем же разобраться, что понимается под родственными словами в современной лингвистике, и чем они отличаются от однокоренных.

Родственные слова: даем определение

Итак, родственными в русском языке называются лексемы:

Например: лес – лесник – лесничий – лесной; ходить – переходить – выход – входивший – вездеход – ходули.

Родственные лексемы могут относиться как к одной, так и к разным частям речи: боль (имя существительное), больной (имя прилагательное), болеть (глагол), больно (наречие). Имея общий корень, а значит, и общей основной смысл, такие слова немного отличаются друга от друга своим лексическим значением.

Тем не менее объяснить оттенки этих значений можно с использованием того этимона, от которого все они образованы. Больной – тот, кто испытывает боль. Болеть – испытывать боль. Больно – так, как ощущается боль.

Важно не путать родственные слова со словоформами. Последние имеют одинаковый корень, но разные окончания (флексии). Солнце – солнца – солнцу; читать – читает – читали – все это не разные лексемы, а формы одного и того же слова. При помощи окончаний меняется только грамматическое значение (падеж, время, лицо, число и т.д.), но лексическое значение остается неизменным.

Однако, чаще всего родственные слова путают с однокоренными. Немногие способны четко объяснить, в чем их отличие. Более того, часто эти понятия используются как синонимы, что не совсем верно.

Для начала вспомним, что однокоренными называются такие слова, которые имеют одинаковый корень, но разные приставки и суффиксы. В отличие от родственных, они необязательно должны быть схожи по своему значению. С этой точки зрения, существительное водитель и прилагательное водяной являются однокоренными, так как у них общий корень – вод. Но они не являются родственными, так как имеют совершенно разное лексическое значение.

Можно сделать следующий вывод: все родственные лексемы – однокоренные, но далеко не все однокоренные слова – родственные.

Об этом важно помнить при подборе проверочного слова, чтобы не ошибиться с объяснением той или иной орфограммы. Часто учащиеся не обращают внимания на смысл лексем и пытаются объяснить написание прилагательного слезливый – существительным слизь, написание существительного пескарь – словом писк.

Правила подбора родственных лексем в русском языке

Рассмотрим правила, которые помогут вам не ошибиться, выполняя подобное задание.

Выделяем корень. Есть два способа сделать это. Первый – понять, как данное слово образовано. Например, строитель – существительное, образованное от глагола строить при помощи суффикса – тель.

Иногда с ходу найти корень не получается. Тогда пробуем изменить начало и конец заданной лексемы: пересказывать – рассказывать, высказывать, сказывать, пересказ, рассказ, сказка, сказочный. Корень здесь – сказ.

Образовываем как можно больше однокоренных слов, не забывая о том, что все они должны быть близки по своему значению.

Здесь нелишним будет напомнить, что в русском языке существует 5 основных способов словообразования:

Существуют и другие, менее распространенные способы словообразования, например, аббревиация (Московский государственный университет – МГУ). Однако для подбора родственных лексем в основном используются способы, перечисленные выше.

Объяснить такие чередования можно исторически. Они связаны с утратой некоторых гласных звуков (льсть – льстить), тождеством согласных звуков (гз, скщ, хш: друг – друзья, писк – пищать, слух – слушать) и другими фонетическими процессами.

Иногда слова, изначально родственные и имеющие один корень, с течением времени расходятся по своему лексическому значению. В современном языке их называют «исторически родственными». В качестве примера можно привести лексемы беда – победа, гвоздь – гвоздика, которые сейчас родственными не считаются, хотя имеют общий корень.

Ну и, наконец, самый главный секрет в деле подбора родственных слов – регулярные тренировки и большой словарный запас. Только в этом случае, проверочные слова будут вспоминаться на автомате, а ваше письмо будет грамотным.

Видео

С помощью этого видео вам будет легче понять, что такое родственные слова и формы слов.

Источник

Однокоренные слова: примеры

Содержание:

Однокоренные слова – слова, имеющие одинаковый корень, объединяющий все лексемы в один смысловой ряд. Так как корень является главной частью слова, передающей основное лексическое значение, то слова с одним корнем схожи по смыслу, однако точное значение немного различается.

При подборе однокоренных слов в корне могут происходить чередования согласных, выпадение или добавление гласных и согласных.

В чем отличие однокоренных слов от родственных?

Не все однокоренные слова являются родственными. Не забываем, что есть такое понятие в русском языке, как омонимичные корни. Один и тот же корень может обозначать абсолютно разное лексическое значение.

При подборе однокоренных родственных слов ВАЖНО четко понимать значение слова. При необходимости лучше обратиться к толковым словарям.

В первом варианте корень –КРАС- имеет основное лексическое значение «привлекательный, приятный вид, впечатляющий»

Во втором случае корень –КРАС- используется в значении «придавать цвет предмету»

Т.к. лексические значения исходного корня абсолютно разные, то и ряды слов нельзя объединять в один.

Еще примеры неродственных слов:

Как отличить однокоренные слова от форм слов?

Для этого нужно хорошо различать словообразующие морфемы от формообразующих.

К словообразующим морфемам относятся:

Они предназначены для образования новых слов.

К формообразующим относятся:

Они образовывают формы одного и того же слова.

Лес – леса, лесу, лесом – окончание образовывает форму числа и падежа существительного

Соберу – собрал – суффикс образовывает форму прошедшего времени глагола

К формам слова относятся слова одной части речи.

Для чего нужно подбирать однокоренные слова?

1. Главный ответ: от этого зависит грамотность.

Правописание гласных или согласных, находящих в слабой позиции в корне слова можно проверить только с помощью однокоренного слова, в котором эти же звуки встанут в сильную позицию. Данное требование применимо при орфограммах «Правописание проверяемых безударных гласных в корне», «Правописание звонких и глухих согласных в корне», «Правописание непроизносимых согласных».

«Проверяемая гласная в корне»

«Правописание звонких и глухих согласных в корне»

«Правописание непроизносимых согласных в корне»

2. Однокоренные слова подбирают для составления словообразовательной цепочки и определения способа образования слова.

Источник

Что такое квадратный корень

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

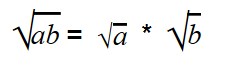Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

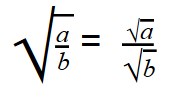Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

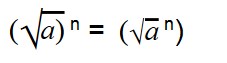Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

Бесплатный марафон Как создавать игры и развиваться в том, что нравится

Источник