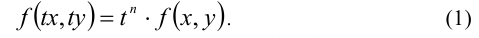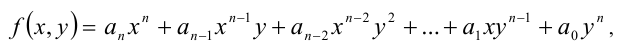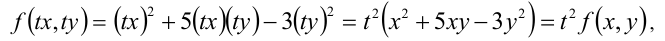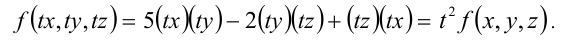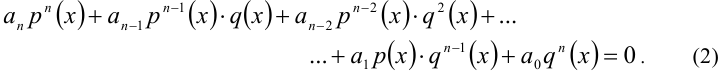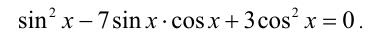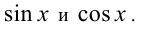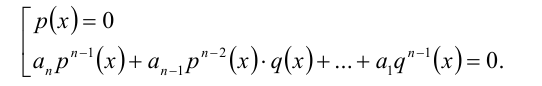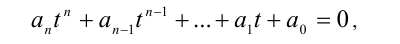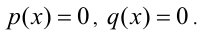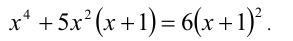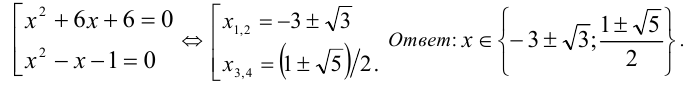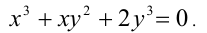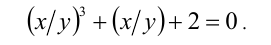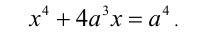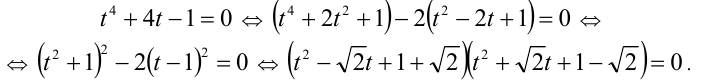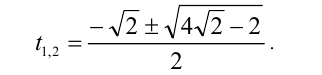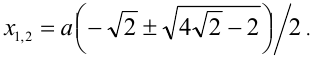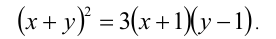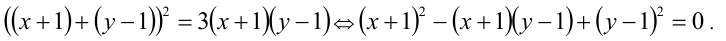Что такое однородное уравнение третьей степени с двумя переменными
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №13. Многочлены от нескольких переменных.
Перечень вопросов, рассматриваемых в теме
1) определение многочлена от нескольких переменных;
2) понятие симметрических многочленов;
3) формулы сокращенного умножения для старших степеней;
5) метод неопределенных коэффициентов.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.
Уравнение Р(x;y) = а, где 
, называютсимметрическим, если Р(х;y) — симметрический многочлен.
Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.
Воспользуемся методом группировки
(x+y+z+u) 2 =((x+y)+(z+u)) 2 = (x+y) 2 +2(x+y)(z+u)+(z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Итак, мы получили (x+y+z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.
2) р(х; у)=3х 2 +5ху-7у 2 — однородный многочлен второй степени; соответственно 3х 2 +5ху-7у 2 =0 — однородное уравнение второй степени.
4) p(x; y)= anx n +an-1x n-1 y+an-2x n-2 y 2 +…+a1xy n-1 +a0y n — общий вид однородного многочлена n-й степени.
Рассмотрим еще один метод разложения многочленов на множители-
метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения
Пример 3. Разложить на множители многочлен
3 x 3 – x 2 – 3 x + 1.
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.
Далее последовательно находим:
Если z=1, то 
, т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.
Ответ: (t; t), где t- любое действительное число.
Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.
x 4 +y 4 = 2xy(x 2 +y 2 )-(x 4 +y 4 )+3(xy) 2 и т.д.
Уравнение Р(x;y) = а, где 
, называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.
А теперь перейдем к такому понятию как бином Ньютона.
Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
(a+b) 4 =(a+b) 3 (a+b)=(a 3 +3a 2 b+3ab 2 +b 3 )(a+b)=a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4
(a+b) 5 =(a+b) 4 (a+b)=(a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 )(a+b)=a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +b 5
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
Общая формула бинома Ньютона:
.
Правая часть формулы называется разложением степени бинома.
— называется биномиальными коэффициентами, а все слагаемые — членами бинома.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Доказать, что значение выражения 5 n +28n-1, где n – натуральное число, делится на 16 без остатка.
Решение: представим первое слагаемое выражение как 5 n = (4+1) n и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16.
Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
Примеры и разборы решения заданий тренировочного модуля
Из данных многочленов выделите симметрические:
Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.
(а+b) 5 = __a 5 +___a 4 b+___a 3 b 2 +___a 2 b 3 +___ab 4 +__b 5
Решение: для решения данного задания воспользуемся треугольником Паскаля
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Нас интересует последняя строчка.
Применив ее, получим ответ:
(а+b) 5 = 1a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +1b 5
Однородные уравнения (ЕГЭ 2022)
В этой статье ты научишься решать однородные уравнения.
В частности, тригонометрические и показательные.
И это не так сложно, как выглядит!
Потому что алгоритм решения однородных уравнений один и тот же!
Для этого эти уравнения и выделили в одну группу – чтобы было легче решать. По одному алгоритму.
Читай статью, решай примеры и все поймешь!
Однородные уравнения — коротко о главном
Определение однородных уравнений
Однородные уравнения – это уравнения вида \( <
_<0>>< ^ >+< _<1>>< ^ >y+< _<2>>< ^ >< ^<2>>+…+< _ >x< ^ >+< _ >< ^ >=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.
Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.
Алгоритм решения однородных уравнений
Однородные уравнение — подробнее
Что такое однородные уравнения? Давай посмотрим на определение.
Однородные уравнения – это уравнения вида \( <
_<0>>< ^ >+< _<1>>< ^ >y+< _<2>>< ^ >< ^<2>>+…+< _ >x< ^ >+< _ >< ^ >=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.
Совершенно пугающее определение, поэтому разберемся на примере.
Пример №1
Это уравнение однородное. Почему? Давай посмотрим на определение.
Стоп! Давай все-таки попытаемся разобраться в этой громоздкой формуле.
На первом месте должна идти первая переменная в степени \( n\) с некоторым коэффициентом. В нашем случае это \( 1\cdot <^<2>>,\ \ k=1,\ \ x=a,\ \ n=2\)
Дальше идет первая переменная в степени \( n-1\) и вторая переменная в первой степени.
Как мы выяснили, \( n=2\), значит здесь степень \( n-1=1\) при первой переменной \( \left( a \right)\) – сходится.
Первая переменная \( \left( a \right)\) в степени \( n-2=0\), и вторая переменная \( \left( b \right)\) в квадрате, с коэффициентом \( \left( 3 \right)\). Это последний член уравнения.
Как видишь, наше уравнение подходит под определение в виде формулы.
Давай рассмотрим вторую (словесную) часть определения.
…с двумя неизвестными, в каждом из слагаемых которого одинаковая сумма степеней этих неизвестных.
У нас две неизвестные \( (a\) и \( b)\). Здесь сходится.
Рассмотрим все слагаемые. В них сумма степеней неизвестных должна быть одинакова.
\( 3<^<2>>\) — сумма степеней равна \( 2\).
Как видишь, все сходится! Это однородное уравнение.
Теперь давай потренируемся в определении однородных уравнений.
Определи какие из уравнений — однородные
Однородные уравнения — уравнения под номерами:
Рассмотрим отдельно \( 11\) уравнение.
Если мы разделим каждое слагаемое на разложим каждое слагаемое, то получим:
А это уравнение полностью попадает под определение однородных уравнений.
Как решать однородные уравнения
Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.
Пример №2
Найдите \( \displaystyle \frac
Разделим уравнение на \( <
Нужно всегда помнить, что делить (и умножать) на переменную мы можем только тогда, когда мы уверены, что эта переменная не может быть равна \( 0\). Например, если нас просят найти \( \frac
\), то мы сразу понимаем, что \( y\ne 0\), поскольку на \( 0\) делить нельзя.
Когда это не так очевидно, необходимо отдельно проверять случай, когда эта переменная равна \( 0\).
У нас по условию y не может быть равен \( 0\). Поэтому мы можем смело делить на \( <
Произведя замену \( t=\frac
Так как это приведенное квадратное уравнение, воспользуемся теоремой Виета:
Произведя обратную замену, получаем ответ
Ответ: \( 2;5\)
Пример №3
Нужно найти: \( \displaystyle \ \frac
Решение:
Разделим уравнение на \( <
Произведем замену \( \displaystyle t=\frac
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №4
Здесь нужно не делить, а умножать.
Умножим все уравнение на \( <
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений ничем не отличается от способов решения, описанных выше.
Только здесь, помимо прочего, нужно немного знать тригонометрию. И уметь решать тригонометрические уравнения (для этого можешь прочитать раздел «Тригонометрические уравнения»).
Рассмотрим такие уравнения на примерах.
Пример №5
Решите уравнение \( <<\sin >^<2>>x-3\sin x\cdot \cos x-4<<\cos >^<2>>x=0\).
Мы видим типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).
Подобные однородные уравнения решаются не сложно, но перед тем, как разделить уравнения на \( <<\cos >^<2>>x\), рассмотрим случай, когда \( \cos x=0\)
В этом случае уравнение примет вид: \( <<\sin >^<2>>x=0\), значит \( \sin x=0\). Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\). Поэтому \( \cos x\ne 0\), и на него можно смело делить:
Сделаем замену \( t=tgx\) и решим квадратное уравнение:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №6
Решите уравнение \( 5<<\sin >^<2>>x-2\sin x\cdot \cos x-3<<\cos >^<2>>x=0\).
Как и в примере \( 5\), нужно разделить уравнение на \( <<\cos >^<2>>x\).
Рассмотрим случай, когда \( \cos x=0\) :
Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\).
Поэтому \( \cos x\ne 0\).
Сделаем замену \( t=tgx\) и решим квадратное уравнение:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение однородных показательных уравнений
Однородные уравнения решаются так же, как рассмотренных выше. Если ты забыл, как решать показательные уравнения – посмотри соответствующий раздел («Показательные уравнения»)!
Рассмотрим несколько примеров.
Пример №7
Мы видим типичное однородное уравнение, с двумя переменными и суммой степеней \( 2x\). Разделим уравнение на \( <<18>^<2x>>\):
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №8
Разделим уравнение на \( <<16>^<2x>>\):
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №9
На примере этой задачи повторим, что такое однородные уравнения и как их решать.
Здесь можно заметить любопытную вещь: если поделить каждое слагаемое на \( <^<2>>\), получим:
То есть, теперь нет отдельных \( a\) и \( b\), – теперь переменной в уравнении является искомая величина \( \frac\). И это обычное квадратное уравнение, которое легко решить с помощью теоремы Виета: произведение корней равно \( 2\), а сумма \( 3\) – это числа \( 2\) и \( 1\).
Ответ: \( 1;\text< >2.\)
называется однородным.
То есть это уравнение с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных. Например, в примере выше эта сумма равна \( 2\).
Решение однородных уравнений осуществляется делением на одну из неизвестных в этой степени:
И последующей заменой переменных: \( t=\frac
Чаще всего нам будут встречаться уравнения второй степени (то есть квадратные), а их решать мы умеем:
\( \displaystyle \Leftrightarrow\ a<
Отметим, что делить (и умножать) все уравнение на переменную можно только если мы убеждены, что эта переменная не может быть равна нулю!
Например, если нас просят найти \( \displaystyle \frac
В случаях, когда это не так очевидно, необходимо отдельно проверять случай когда эта переменная равна нулю. Например:
Решите уравнение \( <<\sin >^<2>>x+3\sin x\cdot \cos x+2<<\cos >^<2>>x=0\).
Пример №10
Видим здесь типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).
Но, прежде чем разделить на \( <<\cos >^<2>>x\) и получить квадратное уравнение относительно \( \displaystyle \frac<\sin x><\cos x>\), мы должны рассмотреть случай, когда \( \cos x=0\).
Однородные уравнения
Однородные уравнения
Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде
где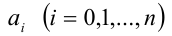 
— коэффициенты многочлена, одновременно не обращающиеся в нуль.
т.е. условие (1) из определения выполняется (n = 2).
Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.
Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве,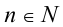 
.
В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида
Оно является однородным тригонометрическим уравнением 2-й степени относительно функций 
Перейдём к процедуре решения уравнения (2).
Если хотя бы один из коэффициентов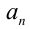 
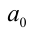
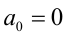
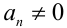
или 
обращается в нуль, то левая часть уравнения легко раскладывается на множители. В результате уравнение оказывается равносильно на ОДЗ совокупности двух уравнений. Например, если 
, 
то получим совокупность
Если же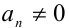 
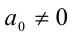
и 
, то для решения однородного уравнения (2) необходимо рассмотреть два возможных случая.
решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.
2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений 
Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.
Пример №185.
Решить уравнение 
Решение:
Пример №186.
Решить в целых числах уравнение 
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть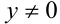 
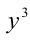
, тогда поделим обе части уравнения на 
:
Ответ: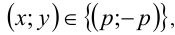 
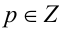
где 
.
Пример №187.
Для каждого действительного значения параметра а решить уравнение
Решение:
Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.
2) Если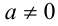 
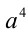
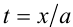
, то поделим на 
, и положим 
:
Первый сомножитель в нуль не обращается, а второй имеет два корня
Ответ: при а = 0 единственное решение x = 0 ;
при 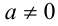два решения 
Пример №188.
Найти действительные корни уравнения
Решение:
Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду
Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.
1) Если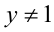 
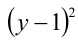
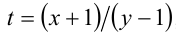
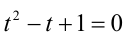
, то, поделив на 
и обозначив 
, получим 
нет решений.
Ответ: 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института