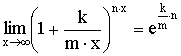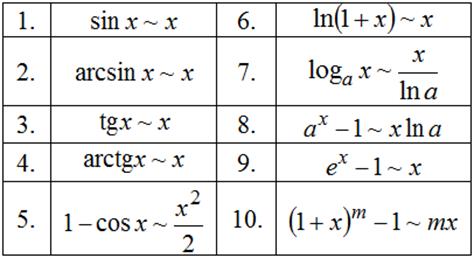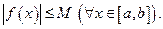Что такое ограниченная и неограниченная функция
Пусть 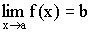

получаем 
Контрольный пример:

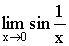
Бесконечно малые и их свойства.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если 


Основные свойства бесконечно малых функций (б.м.)
1° Сумма конечного числа б.м. функций является функцией бесконечно малой.
2° Произведение б функции на ограниченную есть функция бесконечно малая.
3° Произведение двух б.м функций есть функция бесконечно малая..
4° Произведение б.м функции на константу является бесконечно малой функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция бесконечно малая.
6° Функция 
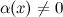
Основные теоремы о пределах.
Теорема 1. Предел суммы равен сумме пределов, если они
существуют:
Доказательство:

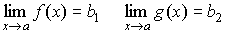
Из теоремы о связи между пределом и бесконечно малой величиной следует:


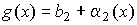
Получаем
Теорема 2. Предел произведения равен произведению пределов, если они существуют: 
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует: 

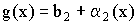
Получаем 
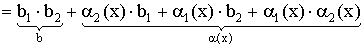


условии: все пределы существуют и 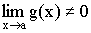
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует:
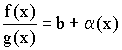

Получаем:
Теорема 4. Предел сохраняет знак неравенства. Если 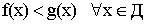

Доказательство:
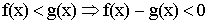
Следовательно, 

Следствие:
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел:
20-21. Первый и второй замечательные пределы и следствия.
Теорема. Первый замечательный предел 
Доказательство (геометрическое):
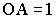
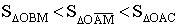

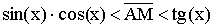
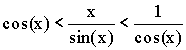

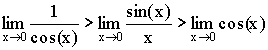
Так как 

Следствия из теоремы:
1) 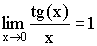
2) 
3) 
4) 
5) 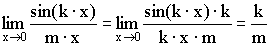
Теорема. Второй замечательный предел 
Доказательство:
Бином Ньютона:

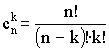
Используем бином Ньютона для доказательства неравенства: 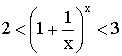

Отсюда заключаем, что 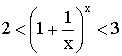
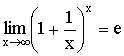
Следствия из теоремы:
1) 
2) 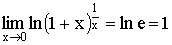
3) 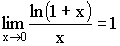
4)
22. Сравнения бесконечно малыхвеличин (б.м.в.) Эквивалентные бесконечно малые.
Непрерывность функции. Определение непрерывности функции в точке и на промежутке. Теорема об арифметических действиях над непрерывными функциями. Непрерывность сложной функции. Ограниченность непрерывной функции.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Функция 

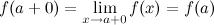
Функция 


Функция 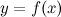
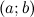
Функция 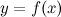

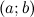




26. Теорема Вейерштрасса об ограниченности функции на замкнутом промежутке.
1) Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
И 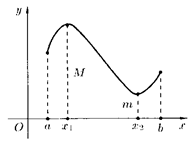
функция 
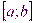
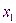



2) Если функция 

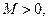
27. Теорема Больцано-Коши о промежуточном значении функции.
Если непрерывная функция, определённая на вещественном интервале, принимает два значения, то она принимает и любое значение между ними.
Следствия теоремы Больцано-Коши
1. Теорема о нуле непрерывной функции.
Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой значение функции равно нулю.
2. В частности любой многочлен нечётной степени имеет, по меньшей мере, один нуль.
§ 05. Свойства функций
Определение 1. Функция 
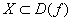
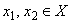
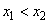
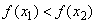
Определение 2. Функция 
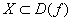
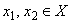
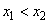
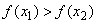
Монотонно возрастающие и монотонно убывающие функции называют монотонными.
Монотонные функции обладают следующими свойствами:
1) сумма двух монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
2) произведение двух положительных монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
3) если функция 
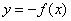
4) если положительная функция 
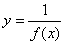
5) если функция 
Определение 3. Функция 
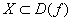
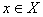

Определение 4. Функция 
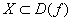
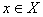
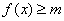
Ограниченная сверху и снизу на множестве Х функция называется ограниченной на этом множестве. Другими словами, если функция 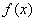
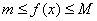
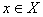
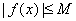
Определение 5. Точка 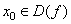

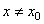
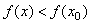
Определение 6. Точка 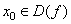

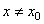
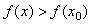
Точки максимума и минимума называют точками Экстремума функции.
Заметим, что функция в области своего определения может иметь несколько точек максимума или минимума.
Определение 7. Будем говорить, что в точке 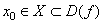

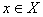
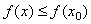
Определение 8. Будем говорить, что в точке 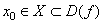

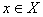
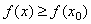
Если множество Х представляет собой отрезок [A; B], то наибольшее и наименьшее значения функция принимает либо в точке экстремума, либо на конце отрезка.
Говорят, что множество Х Симметрично относительно начала координат, если для любой точки 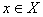
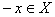
Определение 9. Функция 
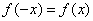
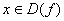
Определение 10. Функция 
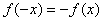
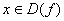
График четной функции имеет ось симметрии: так как точки 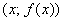
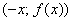
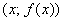
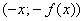
Четные и нечетные функции обладают следующими свойствами:
1) сумма двух четных (нечетных) функций есть функция четная (нечетная);
2) произведение двух четных (нечетных) функций есть функция четная; произведение четной и нечетной функций есть функция нечетная;
3) если нечетная функция 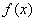
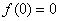
4) всякая функция, определенная на множестве Х, симметричном относительно начала координат может быть представлена в виде суммы двух функций, определенных на Х, причем одна из этих функций является четной, а другая – нечетной.
Определение 11. Функция 
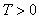
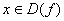
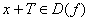
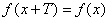
Наименьшее из чисел Т в определении 11 называют Периодом. Периодическая функция имеет бесконечно много периодов, все они кратны числу Т.
Все введенные в этом параграфе определения используются при исследовании функций и построении графиков.