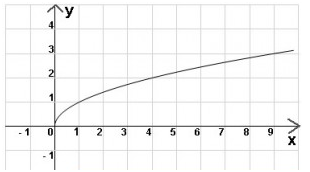
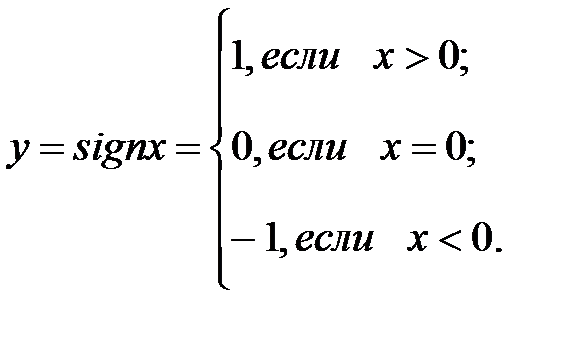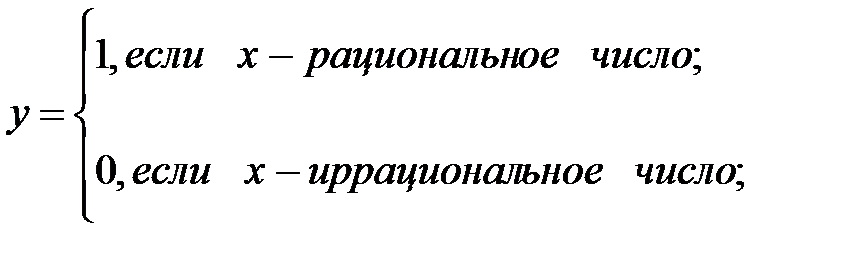Что такое ограниченная сверху функция
§ 05. Свойства функций
Определение 1. Функция 
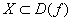
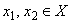
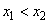
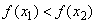
Определение 2. Функция 
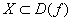
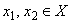
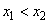
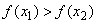
Монотонно возрастающие и монотонно убывающие функции называют монотонными.
Монотонные функции обладают следующими свойствами:
1) сумма двух монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
2) произведение двух положительных монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
3) если функция 
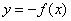
4) если положительная функция 
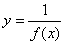
5) если функция 
Определение 3. Функция 
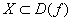
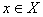

Определение 4. Функция 
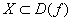
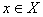
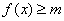
Ограниченная сверху и снизу на множестве Х функция называется ограниченной на этом множестве. Другими словами, если функция 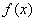
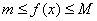
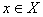
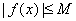
Определение 5. Точка 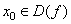

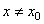
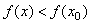
Определение 6. Точка 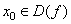

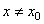
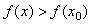
Точки максимума и минимума называют точками Экстремума функции.
Заметим, что функция в области своего определения может иметь несколько точек максимума или минимума.
Определение 7. Будем говорить, что в точке 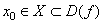

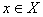
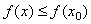
Определение 8. Будем говорить, что в точке 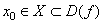

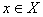
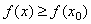
Если множество Х представляет собой отрезок [A; B], то наибольшее и наименьшее значения функция принимает либо в точке экстремума, либо на конце отрезка.
Говорят, что множество Х Симметрично относительно начала координат, если для любой точки 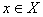
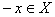
Определение 9. Функция 
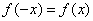
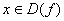
Определение 10. Функция 
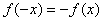
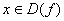
График четной функции имеет ось симметрии: так как точки 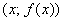
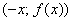
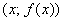
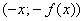
Четные и нечетные функции обладают следующими свойствами:
1) сумма двух четных (нечетных) функций есть функция четная (нечетная);
2) произведение двух четных (нечетных) функций есть функция четная; произведение четной и нечетной функций есть функция нечетная;
3) если нечетная функция 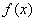
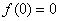
4) всякая функция, определенная на множестве Х, симметричном относительно начала координат может быть представлена в виде суммы двух функций, определенных на Х, причем одна из этих функций является четной, а другая – нечетной.
Определение 11. Функция 
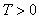
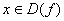
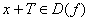
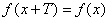
Наименьшее из чисел Т в определении 11 называют Периодом. Периодическая функция имеет бесконечно много периодов, все они кратны числу Т.
Все введенные в этом параграфе определения используются при исследовании функций и построении графиков.
Что такое ограниченная сверху функция
Функция y=f(x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция f(x) ограничена сверху, если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)
· Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)
· Функция f(x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу.
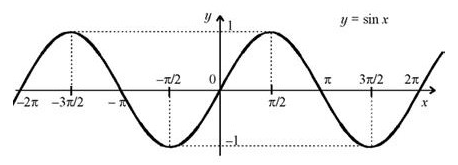
Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x, y=cos x.
При решении уравнений и неравенств свойство ограниченности функций часто играет определяющую роль. Например:
Рассмотрим пример применения данных выводов.
Решение: Функции, записанные в левой и правой частях уравнения, определены при всех действительных значениях х. Кроме того, для любых х верно:
Следовательно, данное уравнение равносильно системе уравнений:
Решения второго уравнения системы есть х=0 и х=-1. Из этих значений первому уравнению удовлетворяет только х=0, которое, следовательно, является единственным решением исходного уравнения.
Ограниченные сверху, снизу и ограниченные функции
Определение №1.Функция 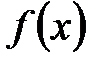
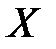
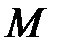
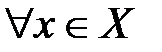
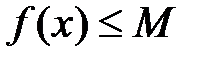
Определение №2.Функция 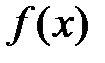
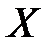
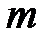
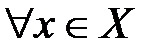
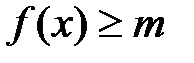
Определение №3. Функция 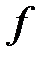
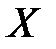
Очевидно, что функция 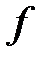
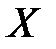
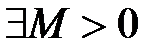
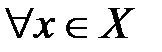
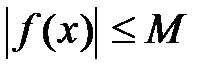
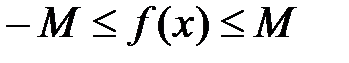
Верхняя и нижняя грани функции
Определение №1.Верхняя грань множества значений 
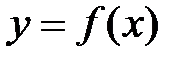
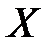
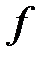
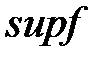
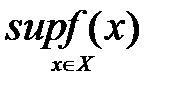
Определение №2. Нижняя грань множества значений 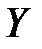
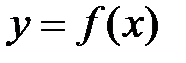
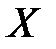
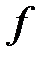
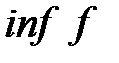
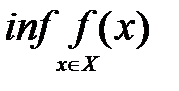
Замечание.1. Верхняя (нижняя) грань функции может быть как конечной, так и бесконечной.
2. Функция ограничена сверху (снизу) на множестве 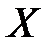
Наибольшие, наименьшие, максимальные, минимальные и экстремальные значения функции
Определение №1.Функция 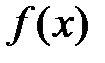
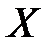
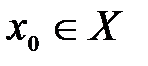
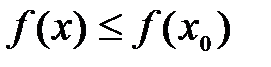
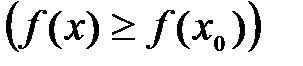
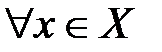
Определение №2.Наибольшие (наименьшие) значения функции называется также максимальным (минимальным) значением и пишется: 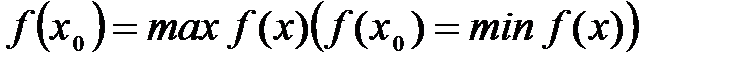
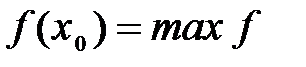
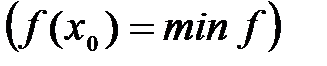
Определение №3. 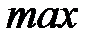
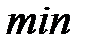
График функции
Определение №1.График функции – это множество пар точек 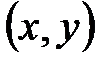
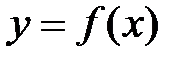
Определение №2.Соотношение 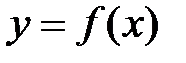
Пример:График функции 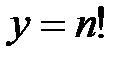
| 8 4 |
| y4 |
| 1! |
| 2! |
| 3! |
| x |
| -1 |
| -1 |
| x1 |
| y1 |
| y2 |
| y |
| x |
Замечание. Не всякая линия является графиком какой-либо одной функции.
Пример.Уравнение окружности 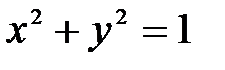

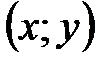
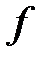
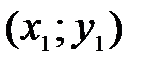
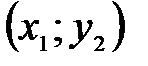
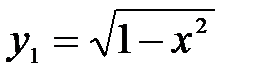
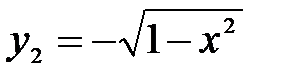
А это противоречит требованию однозначности в определении функций. Но часть окружности, лежащая в нижней полуплоскости, является графиком функции 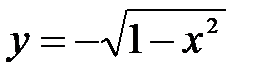
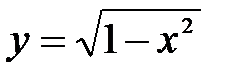
Способы задания функции
Определение.Задать функцию 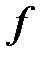
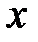
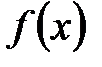
Существует три способа задания функции: аналитический, табличный и графический.
I. Аналитический явный способ задания функции
Сущность способа: Зависимость между переменными величинами определяется с помощью формулы. Она указывает, какие действия надо выполнить, чтобы получить значение функции, соответствующие данному значению аргумента.
Пример: Формула 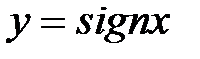
Данная функция задана с помощью нескольких формул. Эта функция определена на всей числовой прямой. А множество ее значений состоит из –1;0;1.
2. Функция Дирихле
определена на всей числовой прямой. А множество ее значений состоит из двух чисел: 1,0. Функцию Дирихле графически изобразить нельзя.
II. Аналитически неявный способ задания функции
1. Неявные функции
Определение.Пусть задано уравнение вида 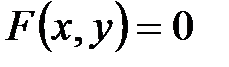
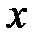
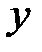
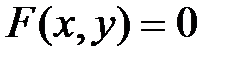
Замечание.1. Термин «неявная» отражает не характер функциональной зависимости, а лишь способ ее задания.
2. Одна и та же функция может быть задана как явно, так и неявно.
Пример: Функции, заданные явно 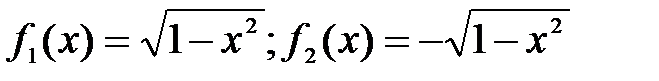

Если заданы функции 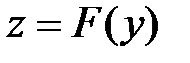
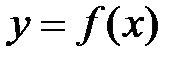
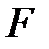
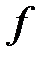
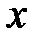
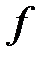
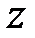
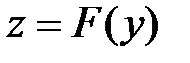
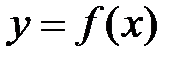
Определение.Функция, определяемая соотношением 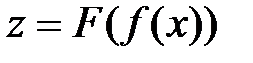
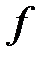
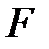
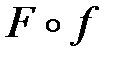
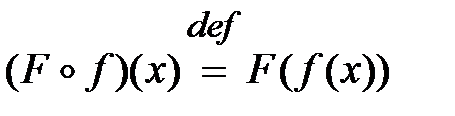
Сложная функция отражает не характер функциональной зависимости, а лишь способ ее задания.
Пример. 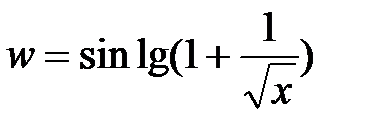
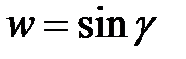
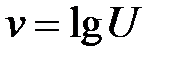
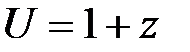
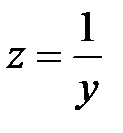
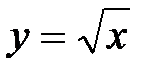
III. Табличный способ задания функции
Пусть дана таблица
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| y | −1 |
Поставим в соответствие каждому значению 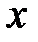
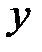
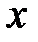
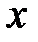
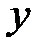
Пример: Таблицы тригонометрических функций; таблицы логарифмов и т.д.
IV. Графический способ задания функции
Соответствие между переменными