Что такое окружность 5 класс
Окружность
Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.
Окружность и овал
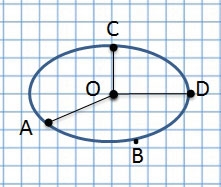
Для начала рассмотрим рисунок и найдём окружность:
Теперь рассмотрим сходства и различия этих геометрических фигур:
Правило:
Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.
Расстояния от центра до линии окружности одинаковые.
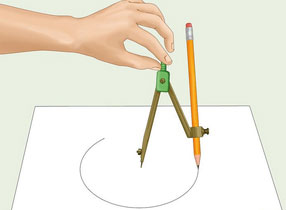
Начертить окружность можно при помощи циркуля:
А овал рисуют от руки:
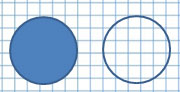
Окружность и круг
Если заполнить пространство внутри окружности, то получим круг.
Круг – это часть плоскости, ограниченная окружностью.
Диаметр и радиус
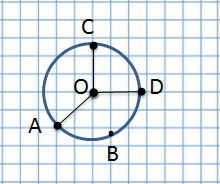
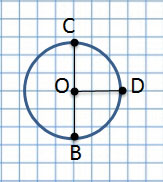
Если соединить центр окружности с линией окружности, получим радиус, например, OC, OA и OD.
Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.
Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.
Поделись с друзьями в социальных сетях:
Окружность и круг. 5-й класс
Класс: 5
Презентация к уроку
Образовательные цели. Обеспечить усвоение учащимися понятий окружности, круга и их элементов (радиуса, диаметра, хорды). Рассмотреть соотношение между диаметром и радиусом окружности.
Развивающие цели. Создать условия для развития у учащихся способностей анализировать и сравнивать предложенные геометрические объекты. Развивать практические умения пользоваться чертежными инструментами.
Воспитательные цели. Способствовать формированию умений работать в группах и индивидуально, осуществлять рефлексию своей деятельности. Создать условия для формирования навыков аккуратного построения фигур.
Метод: исследование с помощью предметных моделей и компьютера.
Тип урока: изучение и первичное закрепление нового материала.
Форма: коллективная и индивидуальная работа.
1. Цели урока.
(Слайд 1) Посмотрите на представленные фотографии и картинки и ответьте на вопрос: что же объединяет все эти предметы?
Математической моделью всех представленных предметов является окружность или круг.
Как вы и догадались тема нашего урока “Окружность и круг”. Откройте тетради и запишите число и тему урока. (Слайд 2). Окружность – удивительно гармоничная фигура, древние греки считали ее самой совершенной. Зная свойства окружности и свойства других линий можно создавать зрительные иллюзии, как, например, на следующих слайдах. (Слайды 4-9).
Сегодня мы научимся различать окружность и круг, дадим определение окружности и всех ее элементов, рассмотрим практические задачи и узнаем много интересных фактов по построению окружности.
2. Мотив деятельности.
На каждой парте перед вами есть круглый предмет, в нашем случае стакан. Берем стакан, ставим на лист бумаги и обводим его маркером.
Ребята, посмотрите какой след оставил маркер?
А теперь возьмите в руки ножницы и аккуратно вырежьте окружность.
Что у вас получилось?
Как вы думаете: сама окружность принадлежит кругу или нет?
Возможно ли построить окружность без циркуля?
Вот несколько примеров, которые я вам продемонстрирую.
С помощью веревки. Берем отрезок веревки, один конец придерживаем пальцем, а другим концом, натягивая веревку и придерживая мел/ручку, чертим окружность.
С помощью расчески. Берем обыкновенную расческу с отверстием на одном конце. Закрепим один край расчески кнопкой (или булавкой) и, вставив между соответствующими зубьями остро заточенный карандаш, поворачиваем расческу и чертим окружность.
Что общего в этих способах построения? (Слайд 11). Запишите определения круга и окружности в тетрадь.
3. Организация учебно-познавательной деятельности учащихся (поисково-исследовательская).
Сегодня на уроке мы с вами научимся чертить окружность с помощью циркуля.
(Слайд 12) Построение окружности радиусом 3 см с помощью циркуля.
А теперь, когда окружность построена в тетрадях, давайте познакомимся с ее основными элементами.
И записываем следующее определение. Отрезок, соединяющий центр окружности с точкой, лежащей на окружности, называется радиусом.
Запишите в тетради равенство, выделенное красным цветом ОА = ОМ = r.
И записываем следующее определение. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр.
Полученное выражение запишите в тетради d = 2r.
И записываем определение. Хорда – это отрезок, соединяющий две точки окружности.
Верно, диаметр – это хорда, проходящая через центр окружности.
(Слайд 18) Давайте закрепим наши полученные знания. Перечислите все радиусы, диаметры и хорды окружности.
(радиусы – OA, OB, OC, OF, OK,
хорды – BL, DF, LE, BF, CK).
4. Совместная деятельность учащихся в структуре урока.
(Слайд 19) Задание 1
Начертите окружность с центром в точке О радиуса 3 см 2 мм.
а) Отметьте точки Р и В, расстояния от которых до точки О равны 3 см 2 мм. Принадлежат ли точки Р и В окружности? Кругу?
б) Отметьте точки А и С, расстояния от которых до точки О равны 2 см 3мм. Принадлежат ли точки А и С окружности? Кругу?
(Слайд 20) Задание 2
Начертите окружность с центром в точке О радиуса 2см 4мм. Проведите две хорды и диаметр. Сравните длины хорд с длиной диаметра.
(Слайд 21) Задание 3
Начертите две окружности с общим центром, такие, что радиус первой окружности равен 4 см и это составляет 2 радиуса второй окружности.
(Слайд 22) Задание 4.
На рисунке диаметр меньшей окружности равен 6 см.
а) Чему равен диаметр большей окружности?
б) Чему равен ее радиус?
5. Индивидуальная работа учащихся в структуре урока.
Ребята, все вы молодцы и хорошо поработали в группах. А теперь давай рассмотрим следующее задание, которое каждый постарается решить сам (Слайд 23). Время на выполнение индивидуального задания 5 минут.
(Учитель ставит песочные часы или будильник, чтобы учащиеся контролировали время).
Обращаю ваше внимание, что любую окружность мы строим по радиусу. Поэтому подумайте, как зная диаметр найти радиус окружности, которую нужно построить.
6. Регулятивные действия учащихся.
Ребята, заканчивая урок, давайте посмотрим со стороны, что мы узнали и чему научились на сегодняшнем уроке. Для этого давайте ответим на следующие вопросы по вариантам (Слайд 24).
7. Домашнее задание.
Для закрепления знаний и умений, полученных на сегодняшнем уроке, дома разберите записанные нами определения и выполните следующие задания в учебнике №406 б, №407 б. (Слайд 25).
Ребята, спасибо за урок (Слайд 26).
Окружность и круг
Содержание
В древние времена люди смотрели на небо и видели там круглое Солнце, круглую Луну. Они придавали кругу мистическое значение и считали его очень красивым. Изображение круга можно увидеть на наскальных рисунках.
Окружность
Судя по древним изображениям, люди изобрели циркуль, с помощью которого можно было чертить ровные круги, уже три тысячи лет назад. Циркуль даже упоминается в мифах Древней Греции.
Если установить ножку циркуля с иглой в какую-либо точку, а ножку с грифелем или карандашом повернуть вокруг той точки, у нас получится замкнутая линия. Она называется окружность.
Окружность состоит из множества точек, расположенных очень близко друг к другу. И какую бы точку на окружности мы не взяли, расстояние от этой точки до центральной точки (той, в которую мы втыкали иглу циркуля) будет одинаковым.
Окружность — замкнутая кривая, которая состоит из всех точек на плоскости, одинаково удалённых от заданной точки, лежащей в той же плоскости, что и кривая; эта точка называется центром окружности.
Радиус
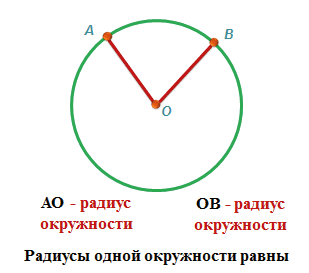
Поставим точку О, затем начертим вокруг неё окружность. На окружности поставим точку А. Это можно сделать в любом месте, где захотите. Теперь соединим точки, у нас получится отрезок ОА. Теперь поставим на окружности вторую точку, В, и тоже соединим её с центром. Сравним отрезки ОА и ОВ. Они равны.
Сколько бы мы ни ставили точек на окружности и сколько бы ни соединяли их с центром, у нас будут получаться равные отрезки.
Отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, называется радиус.
Все радиусы окружности равны между собой.
Латинское слово radius переводится как «спица колеса». Действительно, ведь все спицы у колеса соединены с центром и все равны.
Диаметр
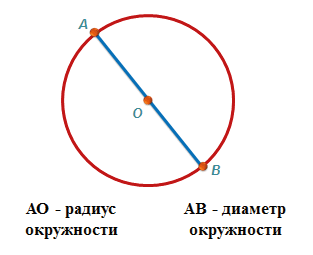
Теперь проведём линию от точки С через центр окружности до её противоположного края. Отрезок СD состоит из двух радиусов: СО и ОD. По размеру он вдвое длиннее радиуса. Такой отрезок называется диаметр.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Помните, мы говорили, что плоскость бесконечна? Но, прочертив на ней окружность, мы делим плоскость на две части. Одна часть – за пределами окружности – так и остаётся бесконечной. А вторая, маленькая, оказывается ограничена пределами окружности и лежит внутри неё.
Часть плоскости вместе с самой окружностью называют кругом.
Это как если бы мы взяли большой лист бумаги, нарисовали на нём кружок и вырезали его ножницами.
Круг тоже состоит из множества точек, и все они лежат на нашей маленькой плоскости. Расстояние от этих точек до центра круга не превышает радиус.
Части круга и окружности
Рассмотрим рисунок 8.
Диаметр разделяет круг на два равных полукруга, а окружность – на две полуокружности.
Часть окружности называется дугой
Теперь мы можем сформулировать определение полукруга и полуокружности:
Полукруг – часть круга, ограниченная диаметром и дугой, лежащей между концами диаметра
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром
Таким образом, полуокружность – это тоже дуга, но не всякая дуга – полуокружность.
Точки А и В на рисунке 10 разделяют окружность на две части, две дуги. Сами точки называют концами дуг.
А вот с таким делением круга, как на рисунке 11, вы наверняка хорошо знакомы. Такой кусочек называется «сектор». Можете попробовать дать определение сектора?
Показать определение сектора
Сектор – часть круга, ограниченная дугой и двумя радиусами
Давайте проверим, хорошо ли вы запомнили части круга.
А вот ещё один хорошо знакомый вам пример окружности – циферблат. Эта окружность разделена на 60 равных делений, и когда минутная стрелка минует очередное деление, это означает, что прошла минута. А больших делений 12, каждое соответствует часу.
«Окружность. Длина окружности», 5-й класс
Разделы: Математика
Класс: 5
Оборудование:
Все перечисленное раздать по количеству подгрупп.
План оформления доски:
| Задача 1. | Окружность | Таблица | Задача 2. |
Таблица:
| Группа № | С (длина окружности) | S (путь) | d (диаметр колеса) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| Т.Н. |
Цель: повторить понятие окружности, ее диаметра; получить формулу длины окружности и научить применять ее при решении задач, число π.
Ход урока
1. Анализ заданий
| Учитель | Дети |
| – На доске изображена геометрическая фигура. Как она называется? | – Окружность. |
| – Дайте определение окружности. | Окружность – это замкнутая линия, все точки которой равноудалены от одной, называемой центром окружности. |
| – Что мы называем ее радиусом? | – Радиус – это расстояние от центра до любой точки окружности. |
| – Что мы называем ее диаметром? | – Диаметр – это отрезок, соединяющий 2 точки окружности и проходящий через центр. |
| – Каким соотношением связаны между собой диаметр и радиус? | – d=2r |
| – Что мы знаем о размере всех d, всех r одной окружности? | – Они равны между собой. |
| –Нам трудно представить свою жизнь без окружности, ведь она является математической моделью многих окружающих нас предметов. Приведите примеры. | – Баранка, обруч, колесо и тд. |
2. Постановка проблемы
| Учитель | Дети |
| –На каждом столе автомашины, моделью каких их частей является окружность? | – Руль, колесо, обода фар и тд. |
| Вашему вниманию предлагается следующая задача (задача 1): Какой путь пройдет ваш автомобиль, если его правое колесо сделает 200 оборотов?Какие варианты решения? | – Измерить длину окружности, проходящей по поверхности колеса и умножить ее на 200. |
| – Молодцы, но для того, чтобы не забыть измеренные величины, я прошу вас записать их в таблицу, лежащую перед вами. А чтобы иметь возможность обобщить эти результаты, я буду заполнять сводную таблицу на доске. | (проводятся измерения, вычисления, заполняются таблицы и сводная таблица на доске (графы С и S)). |
| – Почему получили различные длины окружностей? | – Различные размеры колес. |
| – От чего зависит размер? | – От диаметра. |
| – Молодцы. В Республике Беларусь есть город Жодино. Он известен тем, что там расположен завод, выпускающий карьерные самосвалы марки «БелАз», грузоподъемностью 720 тонн (грузоподъемность Жигулей 440 кг). Внимание вопрос: какой путь пройдет такой самосвал, если правое переднее колесо делает 200 оборотов (диаметр колеса 3,7 метров)? (Задача 2 на доске была закрыта) | – Не знаем как найти длину окружности, чтобы умножить ее на количество оборотов. |
| – Но нам дан диаметр. | – Но неизвестна формула, связывающая диаметр и длину окружности. |
| – Значит, для решения задачи нам нужно установить связь между диаметром и длиной окружности.Значит, тема сегодняшнего урока… | – Нахождение длины окружности, если известен ее диаметр. |
3. Выход из проблемной ситуации
| Учитель | Дети |
| – Измерьте диаметр колес вашего автомобиля. Занесите его в таблицу. | |
| – У каждого автомобиля самая большая длина окружности колеса? | – У того, у кого диаметр больше |
| – Какой вывод можно сделать? | – Чем больше диаметр, тем больше длина окружности. |
| – Посчитайте чему равно отношение С к d? | – Во всех случаях С/d=3 |
| – Оказывается, что если посчитать точнее, то С/d=3, 1/7=3,14159265 C/d=π, C=πd D=2r, C=2 πr | – π=C/d=3,14 |
| – Как связаны между собой d и с? | – Прямопропорционально. |
| – Мы получили формулы, которые связывают длину окружности с диаметром, теперь мы можем вернуться к нашей задаче. S=C*n C=π*d=3,14*3,7=11,618 метров S=2323,6 метров. Значит, чтобы найти длину любой окружности надо знать радиус и знать формулу: C=2πr | – Каждая группа считает самостоятельно |
4. Закрепление пройденного
Найти длину окружности, изображенной на рисунке 12, №№ 850, 851, 852.
Домашнее задание: №№ 868, 869, 873(а,б), 866.
5. Итог урока
чему научились сегодня на уроке? (Находить длину любой окружности, зная ее диаметр по формуле: С=π*d.
Конспект урока математики для 5-го класса по теме «Окружность и круг»
Разделы: Математика
Цели и задачи урока:
Воспитательные: развитие трудолюбия, дисциплинированности, уважения к одноклассникам, формирование интереса к математике.
Средства обучения:
1. Учебники и учебные пособия:
1.1. Учебник. И.И. Зубарева, А.Г. Мордкович “Математика 5”, Мнемозина, Москва, 2008г.;
1.2. Рабочая тетрадь № 1. И.И. Зубарева “Математика 5”, Мнемозина, Москва, 2008г.;
1.3. Методическое пособие для учителя. И.И. Зубарева, А.Г. Мордкович “Математика 5-6 классы”, Мнемозина, Москва, 2008г.
2. Техническое оснащение:
Кабинет информатики, 22 рабочих места, АРМ учителя, проектор, экран.
3. Программное обеспечение: Графический редактор Paint. Программа Microsoft Office Word.
4. Дополнительное оборудование урока.
Бумага, краски, стакан, тарелка из детской посуды, ножницы, циркуль, маркер, линейка, 10 магнитов. Иллюстрации к заданиям (замкнутые, незамкнутые линии), рисунки, выполненные из окружностей. Раздаточный материал: 22 круга из цветной бумаги, 22 окружности, нарисованные на бумаге. Напечатанное слово “циркуль”.
Межпредметная связь: Информатика, русский язык, изобразительное искусство, технология, история.
Ход урока
I. Организация начала урока.
— Здравствуйте ребята! Садитесь. Кто сегодня в классе дежурный?
(Обращение к дежурному).
Кто сегодня отсутствует и по какой причине?
Хорошо, теперь мы начинаем урок.
II. Сообщение темы, задач и целей урока.
— Сегодня мы познакомимся с новыми понятиями: окружность и круг, выясним чем отличаются эти понятия. Ребята, откройте тетради и запишите, число, классная работа и тему урока “Окружность и круг”.
Актуализация знаний. Фронтальный опрос.
1. Какие виды линий изображены ни рисунке 1? На рисунке 2.
(Замкнутые и незамкнутые).
2. Какие геометрические фигуры вы знаете?
3. Какие инструменты необходимы, чтобы изобразить линии и фигуры?
4. Какие единицы длины вы знаете?
III. Изучение нового материала.
Опыты.
Посмотрите, перед вами есть краски, стакан с круглым горлышком, бумага и тарелка с окрашенной водой.
1. Берём стакан, опускаем горлышком в тарелку с окрашенной водой и ставим отпечаток на бумагу. Сделаем так несколько раз. Обратите внимание, какой след оставляет стакан.
2. Берём круглый предмет, в нашем случае тарелка из детской посуды прикладывает к листу бумаги, обводим маркером тарелку.
Ребята, посмотрите какой след оставил маркер. Сравните получившийся результат с первым опытом.
А теперь возьмем ножницы и аккуратно вырежем по той линии, которую оставил маркер.
— Какая фигура у меня получилась?
Дети:
— Круг.
— Правильно!
— Ребята посмотрите, на каждой парте перед вами есть окружность, нарисованная на бумаге и круг из цветной бумаги. Что у них общего? (Ответы детей).
— А чем они отличаются? (Ответы детей).
— Ребята, возьмите ножницы и аккуратно вырежьте окружность. Что у вас получилось? (Ответы детей).
Обратите внимание, что вначале у нас была окружность, но если мы вырежем ее, то получается фигура, которая называется, – круг.
А теперь смотрите, если я сверну круг пополам, то сгиб образует линию, которая разделяет круг на две равные части. Эта линия будет диаметром круга. Диаметр делит круг пополам. Если согнуть круг еще раз пополам, то получатся четыре равные части.
— Ребята, обратите внимание на линии сгиба, они пересеклись в одной точке, эта точка называется центром круга, а линии сгибов – диаметры, они пересекаются и точкой пересечения делятся пополам. Линия, соединяющая центр с краем круга называется радиусом. Обратите внимание, что длины диаметров равны. А что вы можете сказать о длинах радиусов?
Дети:
— Они тоже равны!
— Посмотрите внимательно на окружности, которые получились в результате опытов. Они имеют разные размеры.
Новый материал.
-Как начертить окружность определенного размера?
— Для этого существует инструмент, который называется циркуль.
(Показать инструмент. Показать на доске стихотворение о циркуле).
— Ребята обратите внимание, как пишется слово “циркуль”.
Циркуль.
Циркуль мой, циркач лихой,
Чертит круг одной ногой,
А другой проткнул бумагу,
Уцепился и – ни шагу.
— У циркуля две ножки. На конце одной ножки игла, на конце другой грифель. Ножки циркуля двигаются. (Показываю на доске построение окружности). Для того чтобы начертить окружность надо отметить центр окружности, поставить в центр окружности ножку циркуля с иглой, взять циркуль за хвостик и провести окружность. Острый конец циркуля всегда должен оставаться в одной точке, а расстояние между ножками не должно меняться.
Задание №1
— Ребята, попробуйте начертить окружность в тетради.
(Я выполняю на доске).
— Сначала отметьте центр окружности. Обычно центр окружности обозначают буквой О. Теперь разведите циркуль на некоторое расстояние и начертите окружность. Вспомните, когда мы складывали круг из бумаги пополам, то говорили что линия сгиба это диаметр, он проходит через центр окружности. Давайте построим диаметр окружности. Теперь соединим центр окружности с любой ее точкой. Этот отрезок называется радиусом. Обратите внимание, что точка О делит диаметр на две части и каждая часть является радиусом окружности. Что можно сказать об отношении радиуса и диаметра?
— Диаметр состоит их двух радиусов.
Это отношение можно записать следующим образом.
d = 2r, где диаметр обозначается буквой d, радиус буквой r.
Из этого отношения также следует, что r = d : 2
Как вы думаете, сколько можно провести диаметров, радиусов? (Ответы детей).
Исторические сведения.
— В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. Но еще до колеса люди использовали круглые бревна-катки для перевозки тяжестей. Рисунки на стенах египетских пирамид рассказывают нам, что именно так доставлялись огромные камни на строительство этих пирамид.
— В русском языке слово “круглый” тоже означает высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.
— В школе свойства окружности и круга изучаются до 11 класса, но первые представления у учащихся должны быть уже в 5 классе.
IV. Указание на то, что учащиеся должны запомнить.
— Теперь давайте подведем итоги проведенных опытов.
Окружность – замкнутая линия, все точки которой находятся на одинаковом расстоянии от данной точки. Эта точка называется центром окружности.
Круг – это часть плоскости, которая лежит внутри окружности (вместе с самой окружностью).
Радиус – отрезок, соединяющий центр окружности с точкой на окружности.
Все радиусы окружности равны друг другу.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через центр окружности.
Все радиусы окружности равны друг другу.
Все диаметры окружности равны друг другу.
V. Первичное закрепление изученного материала.
Задание №2
Начертить окружность, радиус которой 2 см. Отметьте диаметр и радиус окружности. Найдите длину диаметра.
— Чтобы выполнить это задание понадобится линейка и циркуль.
— Ребята, как вы думаете для чего нужна линейка? (Ответы детей).
— По линейке отмеряем 2 см. Это радиус окружности. Теперь надо отметить центр окружности, обозначим его буквой О. Начертим окружность. Центр окружности соединим с любой точкой окружности, этот отрезок будет радиусом. Обозначим его буквой r. Теперь проведем диаметр.
— Ребята, как начертить диаметр?
Дети: Диаметр соединяет две точки окружности и проходит через ее центр.
Учитель: Какой буквой обозначается диаметр?
Дети: Диаметр обозначают буквой d.
Задание №3 (устно).
Распределите слова на две группы “Окружность” и “Круг” Объясните свои действия.
(На доске с помощью магнитов прикреплены слова, ученики выходят по одному к доске и распределяют слова по группам, объясняя свой ответ).
Плоская тарелка, блин, пяльцы для вышивания, резинка для волос, компакт-диск, покрышка для колес, обруч (халахуп), кольцо.
Задание №4
Выполнить задание из рабочей тетради по образцу.
§ 23 Окружность и круг. № 23.1. страница 56.
Задание № 405 из учебника (устно).
VI. Физкультминутка.
— Ребята, давайте сделаем разминку. Сядьте ровно.
Тема нашего урока “Окружность и круг” покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим что окружность превратилась в воздушный шарик и отпускаем ее.
VII. Практическая работа на персональных компьютерах. Творческое задание.
— Ребята, следующее задание мы будем выполнять на персональных компьютерах. Ребята сядьте за компьютеры и запустите “Графический редактор Paint”.
— Прежде чем приступить к выполнению задания вспомните инструктаж по технике безопасности, который мы с вами разбирали на уроках информатики.
(Так как ребята хорошо владеют программой, то на выполнение задания достаточно 5 минут).
Задание 1. Нарисуйте окружность любого цвета. Помните, чтобы фигура получилась “правильной”, надо при рисовании удерживать нажатой клавишу Shift.
Задание 2. Нарисуйте круг любого цвета.
Задание 3. Попробуйте придумать и нарисовать рисунок, в котором есть окружности и круги.
(После выполнения задания).
VIII. Итоги урока.
Рефлексия (Приложение 1)
— А теперь продолжите предложения, которые вы видите на экране:
Сегодня я узнал…
Было интересно…
Я понял, что…
Теперь я могу…
Я научился…
У меня получилось…
Я попробую….
Меня удивило…
Мне захотелось…
IX. Домашнее задание.
№ 406 (письменно), повторить № 405 (устно).
Творческое задание. Оценивается отдельно.
Выполнить на альбомных листах. С помощью циркуля создать рисунок из окружностей.