Что такое окружность эйлера

Окружность Эйлера

В геометрии треугольника окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек.

Окружность девяти точек получила такое название из-за следующей теоремы:

Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности.

Окружность девяти точек обладает ещё целым рядом свойств:

Содержание

История

Эйлер в 1765 году доказал, что основания высот и середины сторон лежат на одной окружности (отсюда название «окружность шести точек»). Первое полное доказательство общего результата было, по-видимому, опубликовано в 1821 году, но есть указания на то, что оно было известно и ранее.

См. также

Ссылки

Литература

Полезное

Смотреть что такое «Окружность Эйлера» в других словарях:

Окружность девяти точек — 9 точек Окружность девяти точек это окружность, проходящая через середины всех трёх сторон треугольника. Она также назы … Википедия

Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

ДЕВЯТИ ТОЧЕК ОКРУЖНОСТЬ — окружность Эйлера, окружность, на к роп расположены середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр треугольника с вершинами. Ее радиус равен половине радиуса окружности, описанной около треугольника.… … Математическая энциклопедия

Список объектов, названных в честь Леонарда Эйлера — Существует множество математических и физических объектов, названных в честь Леонарда Эйлера: Содержание 1 Теоремы 2 Лемма 3 Уравнения 4 … Википедия

Интеграл Эйлера — Существует множество математических и физических объектов, названных в честь Леонарда Эйлера: Содержание 1 Теоремы 2 Лемма 3 Уравнения 4 Тождества 5 … Википедия

Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри … Википедия

Теорема Эйлера (планиметрия) — В планиметрии, теорема Эйлера, названная в честь Леонарда Эйлера, утверждает, что расстояние d между центрами вписанной и описанной окружностей треугольника может быть определено по формуле где R и r радиусы, соответственно, описанной и… … Википедия

Описанная окружность — многоугольника окружность, содержащая все вершины многоугольника. Центром является точка (принят … Википедия

Вневписанная окружность — Вписанная (с центром I) и 3 вневписанные (с центрами в J) окружности в Вневписанная … Википедия

Характеристика Эйлера — В алгебраической топологии, эйлерова характеристика есть топологический инвариант (и даже гомотопический инвариант) определённый на большом классе топологических пространств. Обычно эйлерова характеристика пространства X обозначается χ(X).… … Википедия

Источник

Окружность Эйлера и описанная окружность. Теоремы

Прямая Эйлера. Теорема о расположении ортоцентра, точки пересечения медиан, центра описанной окружности и центра окружности 9 точек в треугольнике

Ортоцентр (Н) с центроидом (М), центром описанной окружности (О₁) и центром окружности девяти точек (О) лежат на прямой Эйлера (q).

Окружность Эйлера и описанная окружность

Задача Эйлера. Теорема о точках, лежащих на описанной окружности

В произвольном треугольнике точки, симметричные ортоцентру относительно сторон треугольника и их середин, лежат на описанной окружности.

Н – ортоцентр (точка пересечения перпендикуляров) треугольника АВС;

Р₁ симметрична Н относительно середины стороны ВС точки М₁ (НМ₁=М₁Р₁);

Р₂ симметрична Н относительно середины стороны АС точки М₂ (НМ₂=М₂Р₂);

Р₃ симметрична Н относительно середины стороны АВ точки М₃ (НМ₃=М₃Р₃);

Теорема о радиусах описанной окружности и окружности Эйлера

Радиус окружности Эйлера в два раза меньше радиуса описанной окружности.

Свойство отрезка, проведенного из ортоцентра до пересечения с описанной окружностью

Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.

Н – точка пересечения высот треугольника;

Отрезок НТ – отрезок, соединяющий ортоцентр треугольника АВС с описанной окружностью;

Р – точка пересечения отрезка НТ с окружностью Эйлера:

Теорема о точке пересечения медиан на прямой Эйлера

Точка пересечения медиан лежит о отрезке, соединяющем ортоцентр треугольника с центром описанной окружности, и делит этот отрезок в отношении 1:2, считая от центра описанной окружности:

Средние линии треугольника и окружность Эйлера

Точки, симметричные центру описанной окружности относительно средних линий треугольника лежат на окружности Эйлера.

О – центр описанной вокруг треугольника АВС окружности;

Р₁ симметрична О относительно средней линии М₂М₃ (ОР=РР₁);

Т₁ симметрична О относительно средней линии М₃М₁ (ОТ=ТТ₁);

К₁ симметрична О относительно средней линии М₁М₂ (ОК=КК₁);

Р₁, Т₁ и К₁ – точки, лежащие на окружности Эйлера (окружности 9 точек).

Источник

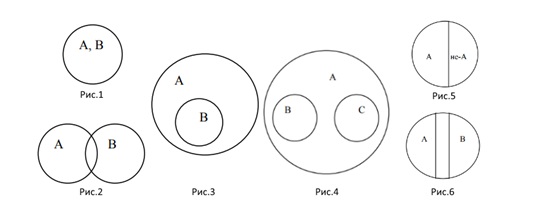
Круги Эйлера и примеры задач на логику

Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.

Описание схемы кругов Эйлера

Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.

Делятся на группы, в зависимости от типа отношений между множествами:

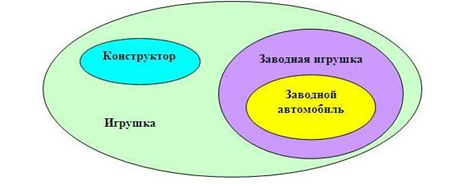
Типовой пример такой диаграммы:

Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.

Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».

Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».

При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.

Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.

Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.

Применение кругов Эйлера

Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.

Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.

Диаграммы делятся на два вида.

Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.

Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров

Примеры задач и решения

Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.

Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.

Задание №1 – начальный уровень.

Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.

Задание №2

Правильный ответ: лягушка.

Задание №3

Правильный ответ: груша.

Задание №4 – средний уровень.

Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.

Задание №5

Правильный ответ: платье.

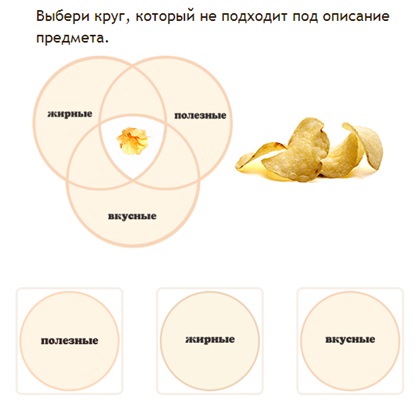
Задание №6

Правильный ответ: полезные.

Задания для школьников

Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.

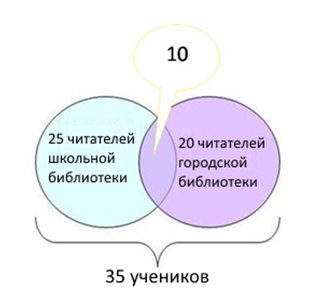
Задание №1

35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.

Ответ:

35 – 20 = 15 – левая сектор голубой зоны.

35 – 20 = 15 – также, левый сектор голубой.

Задание №2 – также предназначено для младших классов, но является более сложным.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.

Ответ:

Все ученики класса – наибольшая окружность.

Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.

Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».

По аналогии, находим количество хоккеистов.

18 – (3 + Z + 5) = 10 – Z.

Чтобы пределить значение Z, нужно суммировать множества учеников.

3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;

Соответственно, Б = 7, Ф = 8, Х = 6.

Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.

Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.

Источник

Лабораторно-практическое занятие с элементами исследования по темам «Прямая Эйлера» и «Окружность Эйлера»

Оборудование:

Цели:

Ход урока

1. Вступительное слово учителя.

В какой-то мере каждый человек способен к творчеству. Однако мера творческих способностей для различных людей различна.

Необходимо направлять сознание на поиск лучшего, более совершенного; развивать чувство неудовлетворённости уже достигнутым; воспитывать в себе привычку к систематическому напряжённому самостоятельному труду.

2 ученик. Несколько шагов по мягкому ковру, несколько взмахов руками. Ломило грудь, ныла поясница, несколько раз мучительно резко потянуло в глазу. Откуда такие немощи? Это в двадцать- то восемь лет! На какой- то миг пронзительно захотелось бросить всё и залечь сурком в тёплую мягкую постель. И отоспаться за все долгие-долгие бессонные ночи. Но это невозможно.

3 ученик. Смешно говорить о честолюбии, но именно оно явилось причиной этой изнурительной спешки. Работа была трудной, даже для него, привыкшего считать безделками то, перед чем другие в бессилии опускали руки. Цифры, цифры, цифры… Колонки цифр, страницы цифр, стопки исписанных страниц. Выкладки и ещё выкладки…

4 ученик (Эйлер). Честь, моя честь, честь ученого, поставлена на карту. Надо за трое суток выполнить, важное правительственное задание, выполнить во что бы то ни стало. Почему я так опрометчиво дал это обязательство? Просили же другие несколько месяцев! Работа и вправду оказалась трудной, но чем труднее, тем заманчивее. Это вызов уму, человеческому уму. Вызов должен быть принят, брошенная перчатка должна быть поднята. Иначе ты окажешься трусом, умственным трусом, что едва ли не хуже, чем быть трусом в поединке по поводу оскорблённой чести.

5 ученик. Математик перчатку поднял. Работа была трудной, но она была и чрезвычайно захватывающей, настолько захватывающей, что математик, забывая о сне и еде, весь отдавался во власть чарующей гармонии строгих и последовательных зависимостей. И снова цифры, формулы, цифры… Эйлер потёр глаз ладонью. Боль, кажется, немножко утихла.

4 ученик (Эйлер). Это – моя жизнь. Без наслаждения музыкой математики она не имеет смысла. Как хорошо сказал кто-то из старых геометров – жизнь хороша тем, что в ней можно заниматься математикой. Как бы порой и не хотелось бросить всё и не думать о гвоздём засевших в голове вопросах…

6 ученик. Работа была окончена в срок. Но оставила после себя страшный, чудовищный след – глаз, его правый глаз, так мучительно нывший в последнее время, не выдержал сверхчеловеческого напряжения и вытек. Но математик не перестал вычислять. А когда вычислять стало уже нельзя, прекратилась и жизнь. После его смерти сказали так: Эйлер перестал вычислять и жить. Именно так – вычислять, а поэтому и жить.

7 ученик. Это был один из величайших математиков всех времен. Родился он в самом начале XVIII ст. в Швейцарии, но почти половину своей долгой жизни прожил в России. Здесь он умер, здесь и покоится его прах. Мы по праву называем Эйлера отечественным математиком.

2. Актуализация знаний.

Каждому ученику предлагается лист с задачами по готовым чертежам для устной работы. Актуализируются следующие знания:
а) признаки подобия треугольников;
б) медианой является множество точек, которое состоит из середин отрезков, параллельных стороне, к которой она проведена;
в) в подобных треугольниках сходственным сторонам пропорциональны:

3. Практическая работа №1. (Прямая Эйлера).

1. На доске построен прямоугольный треугольник. ABC с прямым углом С.

Учитель на данном чертеже строит:

В результате построения наблюдаем, что точки Н(С), М, О лежат на одной прямой.

Как расположены эти точки в остроугольном и тупоугольном треугольниках?

2. Ученикам предлагается провести практическую работу на альбомных листах.

I варианту предлагается остроугольный треугольник;

II варианту – тупоугольный треугольник.

Необходимо построить (алгоритм построения):

Вопросы учителя:

Учителю в начале дискуссии желательно «посеять» сомнения. Для этого нужно найти ту работу, в которой точки не лежат на одной прямой.В результате анализа результатов практической работы ребята приходят к выводу, что в большинстве работ эти три точки лежат на одной прямой(прямой Эйлера), но для того чтобы убедиться в истинности данного утверждения, нужно его доказать.

Впервые эта задача была решена Эйлером в 1765 г. и послужила началом так называемой «геометрии треугольника».

Перед тем, как приступить к доказательству, используя практическую работу, предлагается ответить на вопрос. Какие стороны пересекает прямая Эйлера: а) в остроугольном треугольнике (наибольшую и наименьшую), б) в тупоугольном треугольнике (наибольшую и среднюю)?

4. Доказательство того факта, к которому пришли в результате выполнения практической работы №1.

Доказать, что в любом треугольнике точка пересечения медиан, точка пересечения высот и точка пересечения серединных перпендикуляров к сторонам треугольника лежат на одной прямой (прямой Эйлера).

Дано: М – точка пересечения медиан; Н – точка пересечения высот; О – точка пересечения серединных перпендикуляров. Доказать: О, М, Н лежат на одной прямой.

1. Построим средние линии ∆АВС