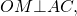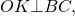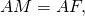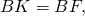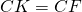Что такое окружность вписанная в треугольник

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

\[ S = \frac<1><2>(a+b+c) \cdot r = pr \]

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

\[ S = \frac<1><2>(a+b+c+d)\cdot r = pr \]

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Источник

Окружность, вписанная в треугольник. Теоремы и их рассмотрение

Вам будет интересно: Казахская академия спорта и туризма. Факультеты, структура вуза

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:

В треугольник можно вписать только одну окружность.

Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:

Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.

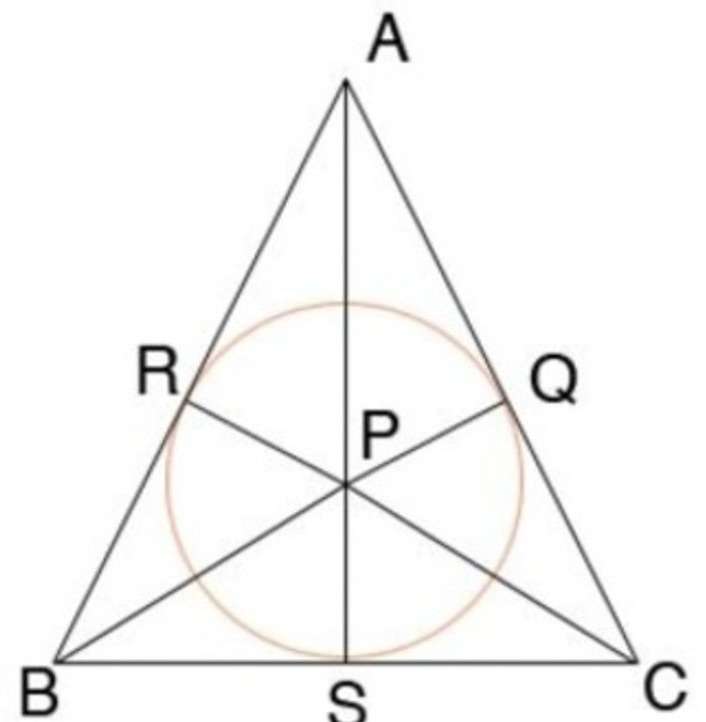
Окружность, вписанная в равнобедренный треугольник

Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.

Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).

Свойства теоремы об окружности, вписанной в треугольник:

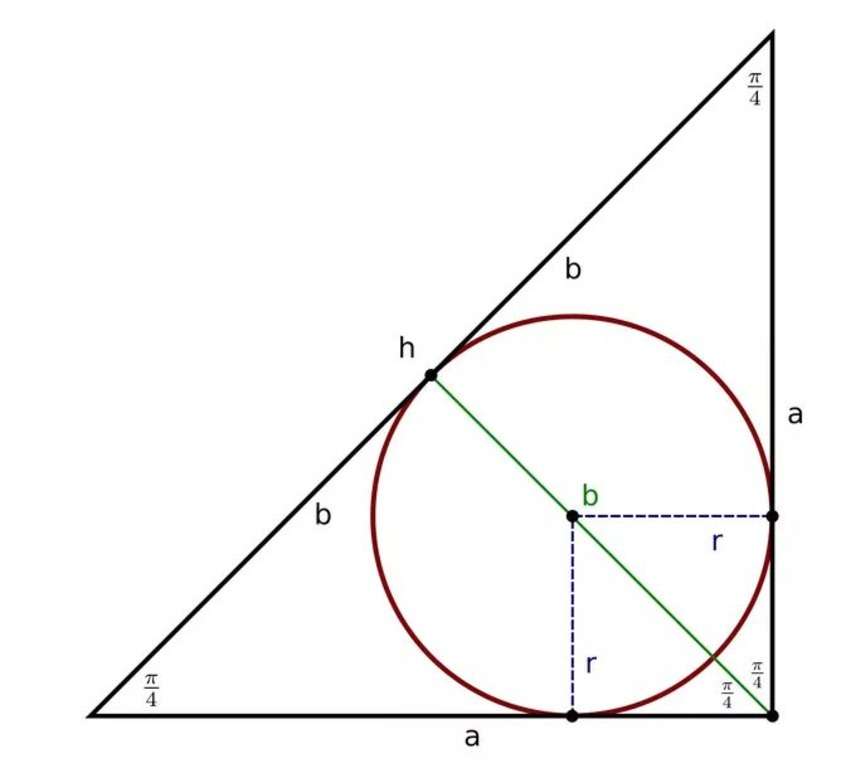
Окружность, вписанная в прямоугольный треугольник

Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.

Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.

Формулировка теоремы о вписанной окружности

В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:

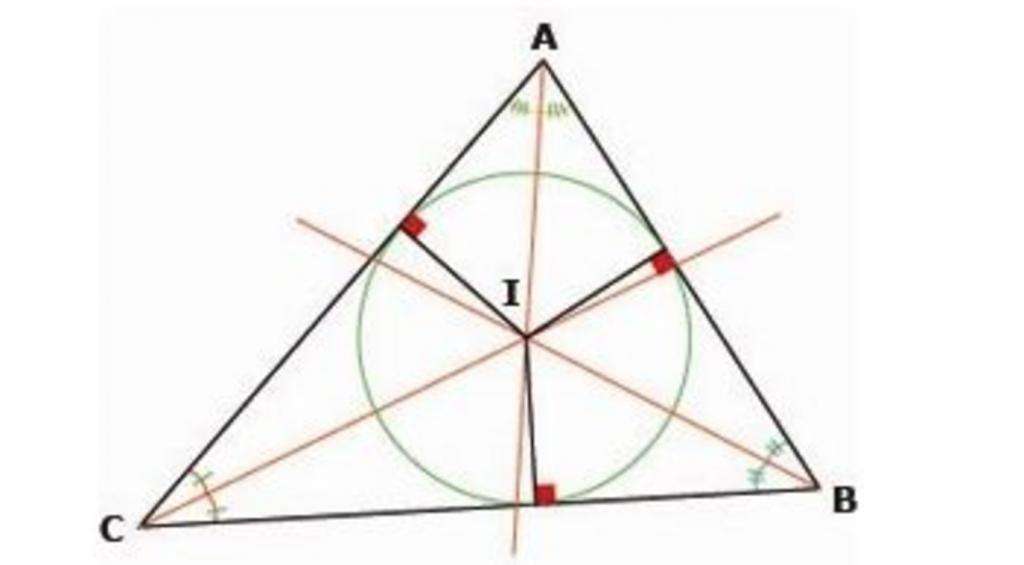
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.

Теорема о центре окружности, вписанной в треугольник

Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.

Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.

Источник

Окружность, вписанная в треугольник

Что такое окружность, вписанная в треугольник? Какие у вписанной окружности свойства?

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Общие точки окружности и треугольника называются точками касания.

Запись окр. (O; r) читают: «Окружность с центром в точке O и радиусом r».

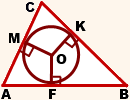
На рисунке окр. (O; r) — вписанная в треугольник ABC.

M, K, F- точки касания.

Свойства вписанной в треугольник окружности.

1) Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

2) Отрезки соединяющие центр вписанной окружности с точками касания, перпендикулярны сторонам треугольника (как радиусы, проведенные в точку касания):

3) Вписанная в треугольник окружность делит стороны треугольника на 3 пары равных отрезков.

(как отрезки касательных, проведенные из одной точки).

Источник

Треугольник вписанный в окружность

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Площадь треугольника

S — площадь треугольника.

\[ S = \frac<1><2>ab \cdot \sin \angle C \]

Периметр треугольника

P — периметр треугольника.

Сторона треугольника

a — сторона треугольника.

Средняя линия треугольника

l — средняя линия треугольника.

Высота треугольника

h — высота треугольника.

\[ h = b \cdot \sin \alpha \]

Свойства

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Источник

Окружность, вписанная в треугольник

Определение окружности, вписанной в треугольник

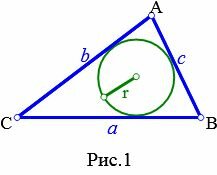
Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).

Можно дать и другое определение окружности, вписанной в треугольник.

Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.

Теорема об окружности, вписанной в треугольник

Теорема 1. В любой треугольник можно вписать окружность.

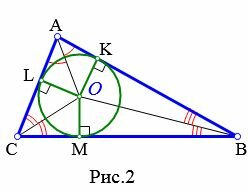Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.

Замечание 1. В любой треугольник можно вписать только одну окружность.

Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.

Источник