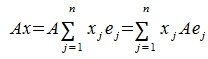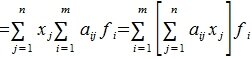Что такое онб в линейной алгебре

Линейная алгебра: пробный заезд

Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.

Часто первое знакомство с линейной алгеброй выглядит как-то так:

Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.

Начнем с практики

Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:

Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.

Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:

где Q_x-h — поток тепла через левую границу, а Q_x+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)

где мы уже учли граничные условия, а q_i=q(x_i). Ну вот мы и получили систему линейных уравнений:

В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:

где a_ij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:

Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.

Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.

Теперь немного теории

Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(α · x + β · y) = α · f(x) + β · f(y) для любых чисел α и β и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.

В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.

Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.

Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)

Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.

Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?

Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.

Википедия Книга — лучший источник знаний

Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.

Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.

Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.

Источник

Линейная алгебра

Лине́йная а́лгебра — часть алгебры, изучающая векторы, векторные, или линейные пространства, линейные отображения и системы линейных уравнений. Векторные пространства встречаются в математике и её приложениях повсеместно. Линейная алгебра широко используется в абстрактной алгебре и функциональном анализе и находит многочисленные приложения в естественных науках.

Содержание

Предмет линейной алгебры

К линейной алгебре относят [1] :

Исторический очерк

См. также

Примечания

Литература

Полезное

Смотреть что такое «Линейная алгебра» в других словарях:

линейная алгебра — Математическая дисциплина, раздел алгебры, содержащий, в частности, теорию линейных уравнений, матриц и определителей, а также теорию векторных (линейных) пространств. Линейная зависимость [linear dependence] «соотношение вида: a1x1 + a2x2 + … +… … Справочник технического переводчика

ЛИНЕЙНАЯ АЛГЕБРА — важная в приложениях часть алгебры, содержащая, в частности, теорию линейных алгебраических уравнений, определителей, матриц … Большой Энциклопедический словарь

линейная алгебра — сущ., кол во синонимов: 1 • линал (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Линейная алгебра — [linear algebra] математическая дисциплина, раздел алгебры, содержащий, в частности, теорию линейных уравнений, матриц и определителей, а также теорию векторных (линейных) пространств … Экономико-математический словарь

ЛИНЕЙНАЯ АЛГЕБРА — раздел алгебры, в к ром изучаются векторные (линейные) пространства, линейные операторы (линейные отображения), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах. Исторически первым разделом Л. а. была … Математическая энциклопедия

ЛИНЕЙНАЯ АЛГЕБРА — численные методы раздел вычислительной математики, посвященный математич. описанию и исследованию процессов численного решения задач линейной алгебры. Среди задач Л. а. наибольшее значение имеют две: решение системы линейных алгебраич. уравнений… … Математическая энциклопедия

линейная алгебра — важная в приложениях часть алгебры, содержащая, в частности, теорию линейных алгебраических уравнений, определений, матриц. * * * ЛИНЕЙНАЯ АЛГЕБРА ЛИНЕЙНАЯ АЛГЕБРА, важная в приложениях часть алгебры, содержащая, в частности, теорию линейных… … Энциклопедический словарь

линейная алгебра — tiesinė algebra statusas T sritis fizika atitikmenys: angl. linear algebra vok. lineare Algebra, f rus. линейная алгебра, f pranc. algèbre linéaire, f … Fizikos terminų žodynas

Линейная алгебра — наиболее важная в приложениях часть алгебры (См. Алгебра). Первым по времени возникновения вопросом, относящимся к Л. а., была теория линейных уравнений (См. Линейное уравнение). Развитие последней привело к созданию теории определителей… … Большая советская энциклопедия

ЛИНЕЙНАЯ АЛГЕБРА — частный случай операторного кольца … Математическая энциклопедия

Источник

Нежное введение в линейную алгебру

Дата публикации 2018-01-26

Что такое линейная алгебра?

Хотя линейная алгебра является большой областью со многими эзотерическими теориями и открытиями, инструментальные средства и обозначения, взятые из этой области, полезны для практиков машинного обучения. Имея прочную основу линейной алгебры, можно сосредоточиться только на хороших или соответствующих деталях.

В этом уроке вы узнаете, что такое линейная алгебра с точки зрения машинного обучения.

После завершения этого урока вы узнаете:

Обзор учебника

Этот урок разделен на 4 части; они есть:

Линейная алгебра

Подобные уравнения являются линейными в том смысле, что они описывают линию на двумерном графе. Линия происходит от вставки различных значений в неизвестный x, чтобы узнать, что уравнение или модель делает со значением y.

Мы можем выстроить систему уравнений одинакового вида с двумя или более неизвестными; например:

Столбец значений y может быть взят в качестве вектора столбца выходных данных уравнения. Два столбца значений с плавающей точкой являются столбцами данных, скажем, a1 и a2, и могут быть приняты в качестве матрицы A. Два неизвестных значения x1 и x2 могут быть взяты в качестве коэффициентов уравнения и вместе образуют вектор неизвестных б предстоит решить. Мы можем написать это компактно, используя линейную алгебраическую запись как:

Проблемы этой формы обычно сложно решить, потому что есть больше неизвестных (здесь у нас есть 2), чем есть уравнения для решения (здесь у нас есть 3). Кроме того, часто не существует ни одной прямой, которая могла бы безошибочно удовлетворить все уравнения. Системы, описывающие проблемы, которые нас часто интересуют (например, линейная регрессия), могут иметь бесконечное число решений.

Это дает небольшой вкус самой сути линейной алгебры, которая интересует нас как практиков машинного обучения. Большая часть остальных операций посвящена тому, чтобы сделать эту проблему и проблемы, такие как ее, легче понять и решить.

Численная линейная алгебра

Применение линейной алгебры в компьютерах часто называют числовой линейной алгеброй.

«Численная» линейная алгебра действительно применяется линейной алгеброй.

Это больше, чем просто реализация операций линейной алгебры в библиотеках кода; это также включает в себя тщательное решение проблем прикладной математики, таких как работа с ограниченной точностью вычислений с плавающей запятой цифровых компьютеров.

Компьютеры хороши в выполнении вычислений линейной алгебры, и большая часть зависимости от графических процессоров (GPU) с помощью современных методов машинного обучения, таких как глубокое обучение, обусловлена ​​их способностью быстро вычислять операции линейной алгебры.

Эффективные реализации векторных и матричных операций изначально были реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большая часть кода или кода, портированного из этих реализаций, лежит в основе большей части линейной алгебры, выполняемой с использованием современных языков программирования, таких как Python.

Три популярные библиотеки числовой линейной алгебры с открытым исходным кодом, которые реализуют эти функции:

Часто, когда вы прямо или косвенно вычисляете операции линейной алгебры с помощью алгоритмов более высокого порядка, ваш код, скорее всего, склоняется к использованию одной из этих или подобных библиотек линейной алгебры. Название одной из этих базовых библиотек может быть вам знакомо, если вы установили или скомпилировали любую из числовых библиотек Python, таких как SciPy и NumPy.

Линейная алгебра и статистика

Линейная алгебра является ценным инструментом в других областях математики, особенно в статистике.

Обычно студенты, изучающие статистику, ожидают увидеть по крайней мере один семестр линейной алгебры (или прикладной алгебры) на уровне бакалавриата.

Влияние линейной алгебры важно учитывать, учитывая фундаментальные отношения, которые обе области имеют с областью прикладного машинного обучения.

Некоторые четкие отпечатки линейной алгебры на статистике и статистических методах включают в себя:

Как видите, современная статистика и анализ данных, по крайней мере, в том, что касается интересов специалиста по машинному обучению, зависят от понимания и инструментов линейной алгебры.

Приложения линейной алгебры

Поскольку линейная алгебра является математикой данных, инструменты линейной алгебры используются во многих областях.

В своей классической книге на тему «Введение в линейную алгебру«Гилберт Странг приводит главу, посвященную применению линейной алгебры. В нем он демонстрирует конкретные математические инструменты, основанные на линейной алгебре. Вкратце они:

Другое интересное применение линейной алгебры состоит в том, что это тип математики, используемый Альбертом Эйнштейном в некоторых частях его теории относительности. Конкретно тензоры и тензорное исчисление. Он также ввел в физику новый тип обозначений линейной алгебры, называемый обозначениями Эйнштейна, или соглашением Эйнштейна о суммировании.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

статьи

Похожие сообщения

Резюме

В этом уроке вы обнаружили нежное введение в линейную алгебру с точки зрения машинного обучения.

В частности, вы узнали:

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Источник

Линейная зависимость и независимость n-мерных векторов

Понятие линейной зависимости и линейной независимости векторов

Для элементов линейного пространства были введены операции умножения вектора на число (из некоторого числового поля) и сложения векторов. При помощи этих операций можно составлять алгебраические выражения.

Набор векторов из пространства называется системой векторов, а любая часть системы векторов – подсистемой.

Система из векторов называется линейно зависимой, если существуют такие числа не все равные нулю одновременно, что справедливо равенство

т.е. линейная комбинация является нулевым вектором.

1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.

2. Понятия линейной зависимости и линейной независимости для векторов определяются также, как для столбцов матриц. Поэтому все свойства, рассмотренные для столбцов матриц, переносятся на векторы. Применение свойств, доказанных для векторов, к столбцам, можно делать без обоснования, так как множество столбцов является линейным пространством (см. пункт 3 в примерах линейных пространств).

Пример 8.1. Установить необходимые и достаточные условия линейной зависимости двух, трех, четырех ненулевых векторов пространства где — множество векторов (направленных отрезков) пространства (см. пункт 2 в примерах линейных пространств).

делаем вывод, что три ненулевых вектора пространства линейно зависимы тогда и только тогда, когда они компланарны.

Свойства линейно зависимых и независимых n-мерных векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов — линейно независима, а после присоединения к ней вектора — оказывается линейно зависимой, то вектор можно разложить по векторам и притом единственным образом, т.е. коэффициенты разложения (8.1) находятся однозначно.

Докажем, например, последнее свойство. Составим линейную комбинацию векторов с коэффициентами и приравняем ее нулевому вектору:

Аффинные, неотрицательные и выпуклые комбинации векторов

Пусть дана система векторов вещественного линейного пространства (т.е. над полем ). Множество линейных комбинаций векторов называется их линейной оболочкой и обозначается:

Понятия линейной, аффинной, конической и выпуклой оболочек, определенные для конечной системы векторов, можно обобщить.

Линейной оболочкой непустого подмножества линейного пространства называется множество всевозможных линейных комбинаций векторов из

Аналогично определяются аффинная, коническая и выпуклая оболочки непустого подмножества

Из определений следуют включения:

Пример 8.2. В пространстве радиус-векторов на плоскости (см. пункт 3 в [url=http://mathhelpplanet.com/static.php?p=linyeinye-prostranstva]примерах линейных пространств[/ur]) даны два неколлинеарных вектора и (рис.8.1).

. При умножении вектора на положительное число его на правление не изменяется. Поэтому вектор при можно рассматривать как сумму двух векторов, принадлежащих лучам и соответственно. По правилу сложения векторов заключаем, Что радиус-вектор лежит либо между этими лучами, либо на одном из них. Следовательно, множество образуют радиус-векторы, концы которых принадлежат углу (заштрихованное множество на рис. 8.1).

2. Свойство 8 линейно зависимых и линейно независимых векторов можно сформулировать так: если каждый вектор системы принадлежит линейной оболочке и k» png;base64,iVBORw0KGgoAAAANSUhEUgAAADYAAAAQBAMAAACvnpHFAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAwBFhiNWgQTAhUbBx7AHm7wHmAAAA3UlEQVQY02NgIB0cE8Ytt/A7bjm2f2gCNgpw5lM5NDnmELhkvwOQ4BDTdNzBI7gALPI4bAJUzr5ATYJB9X32pEDnxz8gQs/FoJL5L8RFGGz04xjkF7D/gqpnly4AUXyBLSx/GCrXL+ALZWCGO5k9sQFIcn51YALS/gqcXxi478HkOMByzB9vgyigpl8M+gmoZrL9Uw1gYGD6wsD2icF+kQCKW94KMMbZMHD9YuAVYPB/YgD2IMwP8x0YBTYxsFxi4D/AUJuC6vf6BubbQNUKDJxAN4MFTeDBAhR6xAAAKHg4VCXzq3kAAAAASUVORK5CYII=» />, то система векторов — линейно зависима.

3. Свойства аффинных оболочек будут рассматриваться в линейных многообразиях. Свойства конических и выпуклых оболочек относятся к выпуклому анализу и применяются в теории оптимизации.

Источник

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

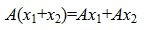,	(2)
.

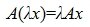Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Источник