Что такое оператор дифференцирования

Производная и оператор дифференцирования

Значение дифференциального и интегрального исчислений сложно переоценить. Фактически современная наука и началась с открытия Ньютоном законов механики и разработки им же соответствующего математического аппарата для анализа следствий этих законов. С тех пор математика была и остается тесно переплетенной с физикой. Иногда для физики используется разработанный математиками аппарат, как в случае с общей теорией относительности Эйнштейна. Иногда физики из своих соображений приходят к новым математическим структурам, например, так было с обобщенными функциями, первую из которых ввел Дирак для нужд квантовой механики.

Производная и интеграл основаны на понятиях о бесконечно малых и возможности деления отрезка до бесконечности. С точки зрения физики существование минимальной длины противоречит теории относительности, ведь разные наблюдатели увидят разную длину. Так же есть веские основания полагать, что деление отрезка до бесконечности тоже невозможно, поскольку понятие длины теряет свой смысл на малых расстояниях (порядка \( \displaystyle 10^<-35>\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.

Производная функции в какой-либо точке по определению это отношение интервала \( \displaystyle \Delta y\) к интервалу \( \displaystyle \Delta x\) в окрестности этой точки, когда длины этих интервалов стремятся к нулю. На рисунке для примера показаны две точки с соответствующими интервалами.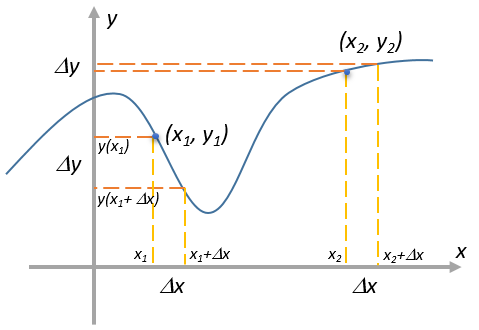

Хотя сами интервалы в пределе бесконечно малы, их отношение в общем случае имеет конечную величину:

\( \displaystyle f'(x)=\frac=\frac<\Delta y><\Delta x>\) при \( \Delta x\rightarrow 0\)

где через \( \displaystyle dx\) и \( \displaystyle dy\) обозначают дифференциалы (difference — разность), то есть те самые бесконечномалые интервалы — разность декартовых координат текущей и следующей точек.

В научной литературе обозначение производной штрихами практически не используется, а запись в виде отношения дифференциалов общепринята. По сути это и есть определение производной.

Из рисунка видно, что даже при одинаковом \( \displaystyle \Delta x\) соответствующая величина \( \displaystyle \Delta y\) будет разной. Каждой точке непрерывной функции \( \displaystyle f(x)\) можно сопоставить число — производную функции в этой точке. Совокупность этих точек тоже будет непрерывной функцией — производной исходной функции.

Физическим смыслом производной является скорость изменения исходной функции. Достаточно взглянуть на рисунок выше чтобы понять. В районе первой точки функция быстро меняется. Производная будет иметь большую величину потому что \( \displaystyle \Delta y\) большое. И она будет отрицательной, так как \( \displaystyle y(x_<1>+\Delta x)

Источник

Что такое оператор дифференцирования

Дифференциальные операторы могут иметь и более сложный вид − в зависимости от образующих их дифференциальных выражений.

В результате действия оператора \(\nabla\) на скалярное поле \(F\) мы получаем градиент поля \(F:\) \[\nabla F = \frac<<\partial F>><<\partial x>>\mathbf + \frac<<\partial F>><<\partial y>>\mathbf + \frac<<\partial F>><<\partial z>>\mathbf.\] Вектор градиента указывает направление наибольшего возрастания функции \(F,\) а его длина показывает скорость возрастания функции в данном направлении.

Рассмотрим некоторые свойства введенного оператора \(L\left( D \right).\)

Оператор \(L\left( D \right)\) является линейным: \[ \left( x \right) + \left( x \right)> \right] > = <L\left( D \right)\left( x \right) + L\left( D \right)\left( x \right).> \]

Коммутативный закон сложения: \[L\left( D \right) + M\left( D \right) = M\left( D \right) + L\left( D \right).\]

Для таких операторов выполняются свойства \(4-6:\)

Коммутативный закон умножения: \[L\left( D \right) \cdot M\left( D \right) = M\left( D \right) \cdot L\left( D \right)\]

Вычислим \(LMy:\) \[My = \left( <2D + 3>\right)y = 2y’ + 3y.\] Получаем следующее дифференциальное выражение: \[ \right) > = <\left( <+ 1> \right)\left( <2y' + 3y>\right) > = <2y''' + 3y'' + 2y' + 3y >= <\left( <2+ 3 + 2D + 3> \right)y.> \] Теперь вычислим \(MLy:\) \[Ly = \left( <+ 1> \right)y = y» + y.\] Следовательно, \[ \right) > = <\left( <2D + 3>\right)\left( \right) > = <2y''' + 3y'' + 2y' + 3y >= <\left( <2+ 3 + 2D + 3> \right)y.> \] Видно, что в данном случае коммутативный закон умножения выполняется (это справедливо для любых операторов \(L\left( D \right)\) с постоянными коэффициентами).

Источник

СОДЕРЖАНИЕ

Определение

Обозначения

При взятии производных более высокого порядка n оператор может быть записан:

Производная функции f от аргумента x иногда задается одним из следующих способов:

В n переменных оператор однородности имеет вид

В письменной форме, следуя общепринятому математическому соглашению, аргумент дифференциального оператора обычно помещается справа от самого оператора. Иногда используется альтернативное обозначение: результат применения оператора к функции в левой части оператора и в правой части оператора, а также разница, полученная при применении дифференциального оператора к функциям с обеих сторон, обозначаются стрелками:

Такое обозначение двунаправленной стрелки часто используется для описания вероятностного тока квантовой механики.

Сопутствующий оператору

Формальное сопряжение по одной переменной

Несколько переменных

Пример

Это свойство можно доказать, используя формальное сопряженное определение выше.

Этот оператор является центральным в теории Штурма – Лиувилля, в которой рассматриваются собственные функции (аналоги собственных векторов ) этого оператора.

Свойства дифференциальных операторов

Любой многочлен в D с коэффициентами функции также дифференциальный оператор. Мы также можем составлять дифференциальные операторы по правилу

Несколько переменных

Кольцо полиномиальных дифференциальных операторов

Кольцо одномерных полиномиальных дифференциальных операторов

Кольцо многомерных полиномиальных дифференциальных операторов

Координатно-независимое описание

Отношение к коммутативной алгебре

Примеры

История

Концептуальный этап написания дифференциального оператора как чего-то отдельного приписывается Луи Франсуа Антуану Арбогасту в 1800 году.

Источник

Линейный оператор

Содержание

Линейный оператор [ править ]

Примеры [ править ]

Тождественный оператор [ править ]

[math]I \colon X \to X[/math] по формуле [math]Ix=x[/math]

Линейный оператор проектирования [ править ]

[math]\mathcal

_^ <||L_2>\colon X \to L_1[/math]

[math]\mathcal

_^ <||L1>\colon X \to L_2[/math]

NB: [math]\mathcal

_>^<||L_<2,1>>\colon X \to X[/math] ( [math]L_1[/math] и [math]L_2[/math] — п.п. [math]X[/math] )

Оператор дифференцирования [ править ]

[math]\mathcal \colon P_n \to P_[/math] по формуле [math](\mathcalp)(t)= = p^<'>(t)[/math]

Интегральный оператор [ править ]

[math](\mathcalf)(s) = \int\limits_a^b K(s,t) \cdot f(t) \cdot dt[/math]

[math]\mathcal \colon C(a,b) \to C(a,b)[/math]

Матрица линейного оператора [ править ]

Пусть п.п. [math]X \leftrightarrow \_^n, \dim X=n[/math]

Пусть п.п. [math]Y \leftrightarrow \_^m, \dim Y = m[/math]

[math] A= \begin \alpha_1^1 & \cdots & \alpha_n^1 \\ \alpha_1^2 & \cdots & \alpha_n^2 \\ \cdots & \cdots & \cdots \\ \alpha_1^m & \cdots & \alpha_n^m \\ \end [/math]

Примеры [ править ]

Нулевой оператор [ править ]

[math] \mathcal_<[m \times n]>= \begin 0 & \cdots & 0 \\ \cdots & \cdots & \cdots \\ 0 & \cdots & 0 \\ \end [/math]

Оператор дифференцирования [ править ]

[math]\mathcal \colon P_n \to P_[/math]

[math] D= \begin 0 & 1 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 2 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 3 &\cdots & 0 \\ \cdots & \cdots & \cdots & \cdots &\cdots & \cdots \\ 0 & 0 & 0 & 0 &\cdots & n \\ \end [/math]

Теорема об эквивалентности задания линейного оператора [ править ]

[math] \Leftarrow x= \sum\limits_^ \xi^i e_i [/math] (единственным образом)

Источник

В математика, а дифференциальный оператор является оператор определяется как функция дифференциация оператор. Полезно, в первую очередь, с точки зрения обозначений, рассматривать дифференциацию как абстрактную операцию, которая принимает функцию и возвращает другую функцию (в стиле функция высшего порядка в Информатика).

В данной статье рассматриваются в основном линейный операторы, которые являются наиболее распространенным типом. Однако нелинейные дифференциальные операторы, такие как Производная Шварца тоже существуют.

Содержание

Определение

Обозначения

Взяв выше, ппроизводные-го порядка оператор можно также записать:

Производная функции ж аргумента Икс иногда дается как одно из следующих:

В D использование и создание нотации приписывается Оливер Хевисайд, который рассматривал дифференциальные операторы вида

Одним из наиболее часто встречающихся дифференциальных операторов является Оператор лапласа, определяется

Иногда это также называют оператор однородности, потому что это собственные функции являются мономы в z:

В п переменных, оператор однородности задается формулой

В письменной форме, следуя общепринятому математическому соглашению, аргумент дифференциального оператора обычно помещается справа от самого оператора. Иногда используется альтернативное обозначение: результат применения оператора к функции слева от оператора и справа от оператора, а также разница, полученная при применении дифференциального оператора к функциям с обеих сторон, обозначаются стрелками следующим образом:

Такое обозначение двунаправленной стрелки часто используется для описания ток вероятности квантовой механики.

Дифференциальный оператор del, также называемый оператор набла, это важный вектор дифференциальный оператор. Часто появляется в физика в таких местах, как дифференциальная форма Уравнения Максвелла. В трехмерном Декартовы координаты, del определяется:

Дел определяет градиент, и используется для расчета завиток, расхождение, и Лапласиан различных объектов.

Сопутствующий оператору

Для линейного дифференциального оператора Т

в сопутствующий этому оператору определяется как оператор Т ∗ < displaystyle T ^ <*>> такой, что

Формальное сопряжение по одной переменной

Эта формула не зависит явно от определения скалярного произведения. Поэтому иногда его выбирают как определение сопряженного оператора. Когда Т ∗ < displaystyle T ^ <*>> определяется по этой формуле, он называется формальный присоединенный из Т.

Несколько переменных

Пример

В Штурм – Лиувилль Оператор является хорошо известным примером формального самосопряженного оператора. Этот линейный дифференциальный оператор второго порядка L можно записать в виде

Это свойство можно доказать, используя формальное сопряженное определение выше.

Этот оператор занимает центральное место в Теория Штурма – Лиувилля где собственные функции (аналоги собственные векторы) этого оператора.

Свойства дифференциальных операторов

куда ж и грамм функции, и а является константой.

Любой многочлен в D с коэффициентами функции также является дифференциальным оператором. Мы также можем составлять дифференциальные операторы по правилу

Затем требуется некоторая осторожность: сначала любые коэффициенты функции в операторе D₂ должно быть дифференцируемый столько раз, сколько применение D₁ требует. Чтобы получить звенеть от таких операторов мы должны предполагать производные всех порядков используемых коэффициентов. Во-вторых, этого кольца не будет коммутативный: оператор gD в целом не то же самое, что Dg. Фактически мы имеем, например, отношение, базовое в квантовая механика:

Подкольцо операторов, являющихся полиномами от D с постоянные коэффициенты является, напротив, коммутативным. Его можно охарактеризовать иначе: он состоит из трансляционно-инвариантных операторов.

Дифференциальные операторы также подчиняются теорема о сдвиге.

Несколько переменных

Такие же конструкции могут быть выполнены с частные производные, дифференцирование по различным переменным, приводящее к коммутирующим операторам (см. симметрия вторых производных).

Кольцо полиномиальных дифференциальных операторов

Кольцо одномерных полиномиальных дифференциальных операторов

Кольцо многомерных полиномиальных дифференциальных операторов

Координатно-независимое описание

куда j k : Γ (E) → Γ (J k (E)) является продолжением, которое ассоциируется с любой частью E это k-джет.

Отношение к коммутативной алгебре

Эта характеризация линейных дифференциальных операторов показывает, что они являются частными отображениями между модули над коммутативным алгебра, позволяя рассматривать концепцию как часть коммутативная алгебра.

Примеры

Этот подход также используется для изучения функций несколько сложных переменных и функции моторная переменная.

История

Концептуальный шаг написания дифференциального оператора как чего-то самостоятельного приписывается Луи Франсуа Антуан Арбогаст в 1800 г. [2]

Источник