Что такое определитель поверхности

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

7.1. Понятия и определения

В начертательной геометрии фигуры задаются графически, поэтому целесообразно рассматривать поверхность как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующейся на таких основных элементарных геометрических понятиях, как точка и множество. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности:

Поверхностью называется непрерывное двупараметрическое множество точек.

Для получения наглядного изображения поверхности на чертеже закон перемещения линии целесообразно задавать графически в виде совокупности линий и указаний о характере перемещения линии. Эти указания могут быть заданы графически, в частности с помощью направляющей поверхности. В процессе образования поверхностей линия может оставаться неизменной или менять свою форму. Такой способ образования поверхности называется кинематическим, а сама поверхность − кинематической. Закон перемещения образующей линии, как правило, задается при помощи направляющих линий и алгоритма перемещения образующей по направляющим.

На чертеже кинематическая кривая поверхность задается при помощи ее определителя. Определителем поверхности называют совокупность условий, необходимых и достаточных для задания поверхности в пространстве.

Подвижная линия называется образующей, неподвижные линии и поверхность – направляющими.

Примером такого способа образования могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» профиля резца.

Режущие кромки являются неотъемлемой частью исполнительных механизмов многих строительных и дорожных машин, применяемых не только для разработки и перемещения грунта (бульдозеры, грейдеры и т. п.), но и рытье траншей, котлованов, проходка траншей, профилирование откосов и многое другое.

Но режущие кромки во многих случаях начинают уступать место производящей поверхности, с которой связано развитие прогрессивных производительных процессов обработки металлов давлением и обкаткой. Геометрическая сущность этих процессов – метод огибания.

Рассмотрим некоторые кривые поверхности.

Кривые поверхности широко применяются в различных областях науки и техники при создании очертаний различных технических форм или как объекты инженерных исследований. Существуют три способа задания кривых поверхностей:

2. При помощи каркаса;

3. Кинематический, т. е. перемещением линий в пространстве.

.

Рис. 7.1. Пример поверхности, заданной аналитически

Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает кривую поверхность как множество точек, координаты которых удовлетворяют некоторому уравнению. На рис. 7.1 приведен пример поверхности, за­данной аналитически (системой алгебраических уравнений).

При каркасном способе задания кривая поверхность задается совокупностью некоторого количества линий, принадлежащих поверхности.

Каркас поверхности

Другим способом образования поверхности и ее изображения на чертеже может служить каркас поверхности.

Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности.

В зависимости от того, чем задается каркас поверхности, точками или линиями, каркасы называют точечными или линейными. Линейным каркасом называется множество таких линий, которые имеют единый закон образования и связаны между собой определенной зависимостью. Условия связи между линиями каркаса называются зависимостью каркаса. Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса. Если параметр линейного каркаса является непрерывной функцией, то каркас называется непрерывным, а если параметр − прерывная функция, то каркас называется дискретным.

На рис. 7.2 приведен пример каркаса поверхности, состоящей из двух ортогонально расположенных семейств линий а₁, а₂, а₃,…, а_n, b₁, b₂, b₃,…b_n.

.

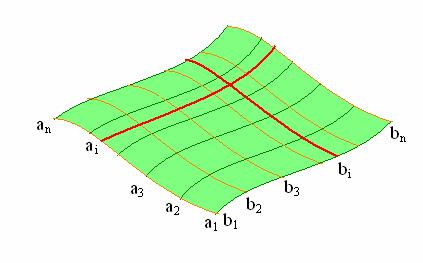
Рис. 7.2. Пример линейного каркаса поверхности

Определитель поверхности

Кинематический способ образования поверхности можно представить как множество положений движущейся линии или поверхности.

Этот способ дает возможность сформулировать понятие определителя поверхности. Под этим понятием обычно подразумевают необходимую и достаточную совокупность геометрических фигур и кинематических связей между ними, которые однозначно определяют поверхность.

Определитель поверхности состоит из двух частей:

Чтобы найти определитель поверхности, следует исходить из кинематического способа образования поверхности.

Для того чтобы построить чертеж поверхности, необходимо предварительно выявить ее определитель. Определитель поверхности выявляется путем анализа способов образования поверхности или ее основных свойств. В общем случае поверхность может быть образована несколькими способами и поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший.

Поверхность считается заданной на комплексном чертеже, если относительно любой точки пространства, заданной на чертеже, можно однозначно решить вопрос о принадлежности ее данной поверхности. Построение проекций любых точек и линий, принадлежащих поверхности, а также второй их проекции, если одна задана, выполняется на основании ее определителя.

Точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности.

Рассмотрим примеры выявления определителя для некоторых простейших поверхностей:

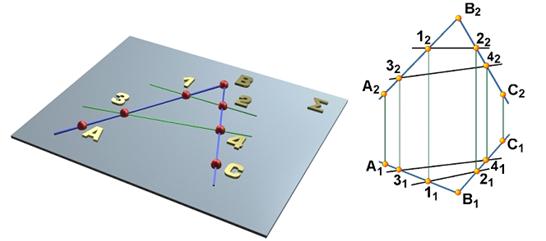
Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну и только одну плоскость ( 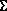на рис. 7.3, а). Точки А, В и С составляют геометрическую часть определителя плоскости.

Вторая часть определителя, т. е. алгоритм построения в плоскости 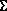(А, В, С) любых линий и точек, выражается рассмотренными ранее условиями принадлежности прямой и точки плоскости.

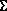
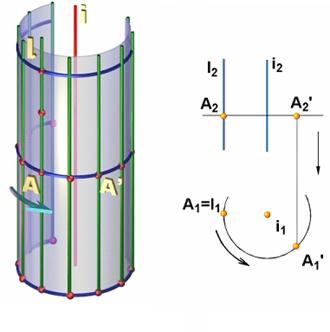
На чертеже (рис. 7.3, б) плоскость задана проекциями геометрической части своего определителя: А(А₁А₂), В(В₁В₂), С(С₁С₂).

Цилиндрическая поверхность вращения может быть образована вращением прямой l i вокруг оси i (рис. 7.4, а).

Геометрическая часть определителя поверхности состоит из образующей l и оси i. Алгоритмическая часть определителя состоит из операции вращения образующей линии l вокруг оси i.

Определитель цилиндрической поверхности вращения имеет вид Ф(l i, i) [А]. На чертеже (рис. 7.4, б) цилиндр вращения задан проекциями геометрической части своего определителя.

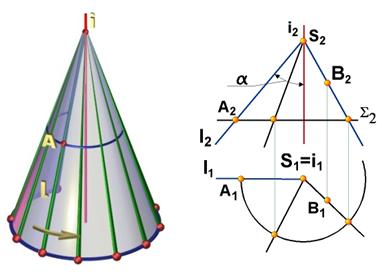
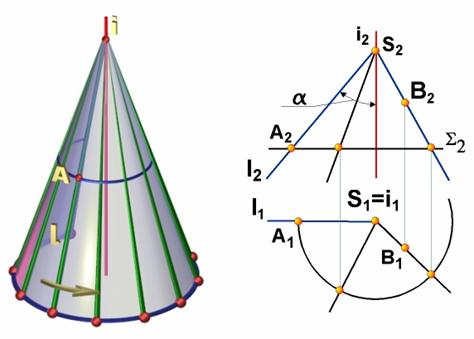
Коническая поверхность вращения может быть образована вращением прямой l, пересекающей ось вращения i под некоторым углом (рис. 7.5, а). Алгоритмическая часть определителя состоит из словесного указания о том, что поверхность образуется вращением образующей l вокруг оси i.

.

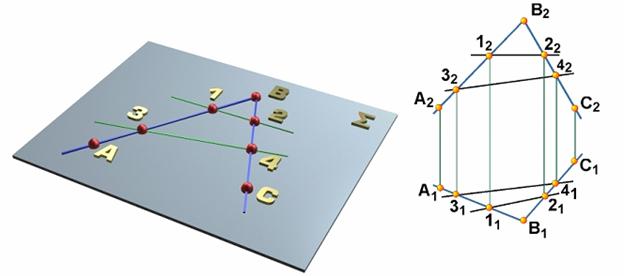
Рис.7.3. Примеры определителя: а − алгоритмическая часть; б − геометрическая часть

Определитель конической поверхности вращения имеет вид Ф(l i)[A].

На чертеже (рис. 7.5, б) конус вращения задан проекциями геометрической части его определителя:

l(l₁l₂) i(i₁i₂>

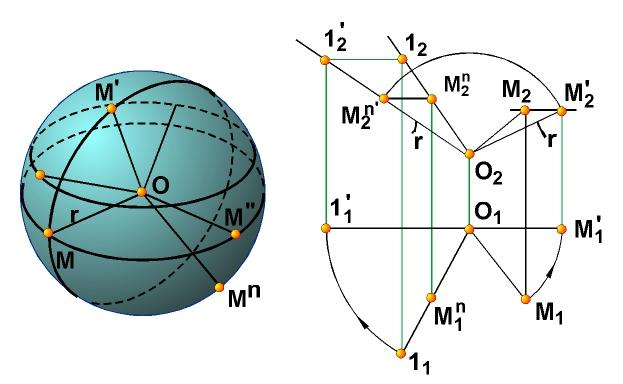
В указанных примерах определитель поверхности выявляется путем анализа способов ее образования. Рассмотрим пример выявления определителя поверхности путем анализа ее основных свойств. Возьмем, например, сферу. Сферой называется поверхность, образованная множеством точек пространства, находящихся на расстоянии | r | от данной точки O (рис. 7.6, а). Геометрическая часть определителя сферы состоит из точки O (центра сферы) и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладывания на ней от точки О отрезка | OM’ = | ОМ | = | r |. Определитель сферы имеет вид Ф(О, М) [А].

.

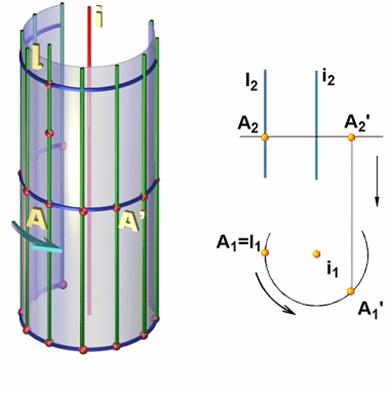
На рис. 7.6, б (справа) сфера задана проекциями точек О(O₁O₂) и М(М₁М₂), которые составляют геометрическую часть ее определителя, и показано построение произвольной точки М n (М n ₁ М n ₂)сферы.

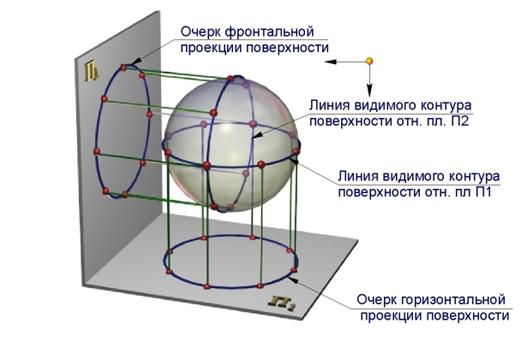
При чтении чертежа немаловажную роль играет его наглядность. Задание поверхности проекциями геометрической части ее определителя не обеспечивает наглядности изображений. Поэтому для придания чертежу поверхности большей наглядности и выразительности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих.

При проецировании поверхности на какую-либо плоскость проекций часть проецирующих лучей касается ее, образуя проецирующую поверхность. Точки касания при этом образуют линию видимого контура поверхности относительно этой плоскости проекций (рис. 7.7). Очерк проекции поверхности является проекцией соответствующей линии видимого контура.

Линия видимого контура поверхности разделяет ее на две части − видимую, обращенную к наблюдателю, и невидимую. Никакая точка поверхности не может спроецироваться за пределы очерка.

.

На чертежах (рис. 7.8, а, в) конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах (рис. 7.8, б, г) для тех же поверхностей построены очерки их проекций. Последние, безусловно, обладают большей наглядностью и выразительностью.

Кривые поверхности разделяются на линейчатые и нелинейчатые, закономерные и незакономерные. Поверхность называется линейчатой, если она может быть образована перемещением прямой линии, в противном случае − нелинейчатой.

Если поверхность может быть задана каким-либо уравнением, она называется закономерной, в противном случае − незакономерной, или графической (задается только чертежом).

Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические и трансцендентные.

Алгебраическое уравнение n-й степени (в декартовых координатах) задает алгебраическую поверхность n-го порядка (трансцендентные поверхности порядка не имеют). Алгебраическая поверхность n-го порядка пересекается плоскостью по кривой n-го порядка, а с прямой линией − в n точках.

.

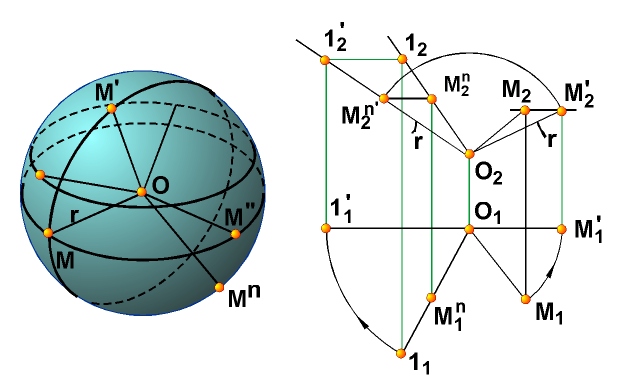
Рис. 7.6. Изображение определителя сферы: а – алгоритмическая часть; б – геометрическая часть

Плоскость, имеющую уравнение первой степени (с произвольной плоскостью пересекается по прямой линии, а с прямой − в одной точке), можно рассматривать как поверхность первого порядка. Примерами кривых поверхностей второго порядка могут служить поверхности, образованные вращением кривых второго порядка вокруг одной из своих осей.

Поверхности второго порядка пересекаются с произвольной плоскостью по кривым второго порядка, а с прямой − в двух точках. Примером поверхности четвертого порядка может служить тор (см. поверхности вращения).

.

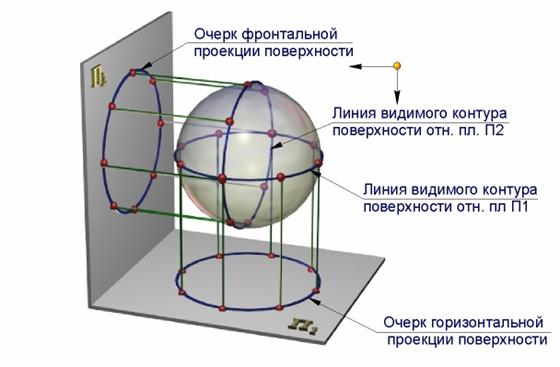
Рис. 7.7. Образование проекций сферы

.

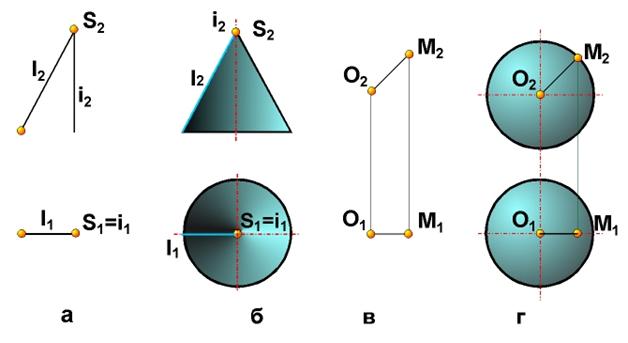
Рис. 7.8. а, в − проекции геометрической части определителей конуса и сферы; б, г − очерки проекций конуса и сферы

Определитель может быть положен в основу классификации поверхностей. К одному и тому же классу относятся поверхности, имеющие одинаковую структуру определителя.

Наибольшее применение в технике получили кинематические кривые поверхности с образующими постоянной формы:

1. Линейчатые поверхности:

Источник

Определитель поверхности

Кинематический способ образования поверхности можно представить как множество положений движущейся линии или поверхности.

Этот способ дает возможность сформулировать понятие определителя поверхности. Под этим понятием обычно подразумевают необходимую и достаточную совокупность геометрических фигур и кинематических связей между ними, которые однозначно определяют поверхность.

Определитель поверхности состоит из двух частей:

Чтобы найти определитель поверхности, следует исходить из кинематического способа образования поверхности.

Для того чтобы построить чертеж поверхности, необходимо предварительно выявить ее определитель. Определитель поверхности выявляется путем анализа способов образования поверхности или ее основных свойств. В общем случае поверхность может быть образована несколькими способами и поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший.

Поверхность считается заданной на комплексном чертеже, если относительно любой точки пространства, заданной на чертеже, можно однозначно решить вопрос о принадлежности ее данной поверхности. Построение проекций любых точек и линий, принадлежащих поверхности, а также второй их проекции, если одна задана, выполняется на основании ее определителя.

Точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности.

Рассмотрим примеры выявления определителя для некоторых простейших поверхностей:

Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну и только одну плоскость ( на рис. 7.3, а). Точки А, В и С составляют геометрическую часть определителя плоскости.

Вторая часть определителя, т. е. алгоритм построения в плоскости (А, В, С) любых линий и точек, выражается рассмотренными ранее условиями принадлежности прямой и точки плоскости.

На чертеже (рис. 7.3, б) плоскость задана проекциями геометрической части своего определителя: А(А₁А₂), В(В₁В₂), С(С₁С₂).

Цилиндрическая поверхность вращения может быть образована вращением прямой 1 || i вокруг оси i (рис. 7.4, а).

Геометрическая часть определителя поверхности состоит из образующей 1 и оси i. Алгоритмическая часть определителя состоит из операции вращения образующей линии 1 вокруг оси i.

Определитель цилиндрической поверхности вращения имеет вид Ф(l i, i) [А]. На чертеже (рис. 7.4, б) цилиндр вращения задан проекциями геометрической части своего определителя.

Коническая поверхность вращения может быть образована вращением прямой l, пересекающей ось вращения i под некоторым углом (рис. 7.5, а). Алгоритмическая часть определителя состоит из словесного указания о том, что поверхность образуется вращением образующей l вокруг оси i.

Определитель конической поверхности вращения имеет вид Ф( l ∩ i)[A].

На чертеже (рис. 7.5, б) конус вращения задан проекциями геометрической части его определителя:

В указанных примерах определитель поверхности выявляется путем анализа способов ее образования. Рассмотрим пример выявления определителя поверхности путем анализа ее основных свойств. Возьмем, например, сферу.Сферой называется поверхность, образованная множеством точек пространства, находящихся на расстоянии | r | от данной точки O (рис. 7.6, а).Геометрическая часть определителя сферы состоит из точки O (центра сферы) и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладывания на ней от точки О отрезка | OM’ = | ОМ | = | r |. Определитель сферы имеет вид Ф(О, М) [А]. На рис. 7.6, б (справа) сфера задана проекциями точек О(O₁O₂) и М(М₁М₂), которые составляют геометрическую часть ее определителя, и показано построение произвольной точки М n (М n ₁ М n ₂) сферы. При чтении чертежа немаловажную роль играет его наглядность. Задание поверхности проекциями геометрической части ее определителя не обеспечивает наглядности изображений. Поэтому для придания чертежу поверхности большей наглядности и выразительности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих.

Рис. 7.5. Изображение определителя конической поверхности:

На чертежах (рис. 7.8, а, в) конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах (рис. 7.8, б, г) для тех же поверхностей построены очерки их проекций. Последние, безусловно, обладают большей наглядностью и выразительностью.

Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические и трансцендентные.

Рис. 7.7. Образование проекций сферы

Определитель может быть положен в основу классификации поверхностей. К одному и тому же классу относятся поверхности, имеющие одинаковую структуру определителя.

Наибольшее применение в технике получили кинематические кривые поверхности с образующими постоянной формы:

1. Линейчатые поверхности:

Источник

Что такое определитель поверхности

Основные понятия и определения

Поверхность как объект инженерного исследования может быть задана следующими основными способами: а) уравнением; б) каркасом; в) определи гелем; г) очерком.

Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает поверхность как множество точек, координаты которых удовлетворяют уравнению вида F (х,у, z) = 0.

В начертательной геометрии поверхность на чертеже задается каркасом, определителем, очерком.

Поверхность, образованная движущейся в пространстве линией, на чертеже может быть задана определителем поверхности.

Определителем поверхности называется совокупность геометрических фигур и связей между ними. позволяющих однозначно образовать поверхность в пространстве и задать ее на чертеже.

Способ образования поверхности движущейся в просфанстве линией называют кинематическим.

Линию, образующую при своем движении в пространстве данную поверхность называют образующей (производящей).

Образующая при своем движении может изменять свою форму или оставаться неизменной. Закон перемещения образующей можно, в частности, задать неподвижными линиями, на которые при своем движении опирается образующая. Эти линии называются направляющими.

На чертеже при задании поверхности ее определителем строятся проекции направляющих линий, указывается, как находятся проекции образующей линии. Построив ряд положений образующей линии, получим каркас поверхности. Пример образования поверхности кинематическим способом показан на рис. 96.

В качестве образующей а этой поверхности взята плоская кривая. Закон перемещения образующей задан двумя направляющими m и n и плоскостью а. Образующая а скользит по направляющим, все время оставаясь параллельной плоскости a.

Определитель поверхности выявляется путем анализа способов образования поверхности или се основных свойств. В общем случае одна и та же поверхность может быть образована несколькими способами, поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший. Например, боковая поверхность прямого кругового цилиндра может быть образована четырьмя способами (рис. 97):

а) как след, оставляемый в пространстве прямой а при ее вращении вокруг оси m (рис. 97,а).

б) как след, оставляемый в пространстве кривой линией b при ее вращении вокруг оси m (рис. 97,6).

в) как след, оставляемый в пространстве окружностью с при поступательном перемещении ее центра О вдоль оси m. при этом плоскость окружности все время остается перпендикулярной к этой оси (рис. 97,в).

г) как огибающую всех положений сферической поверхности р постоянного радиуса, центр которой перемещается по оси m (рис.97,г).

Наиболее простым из рассматриваемых будет определитель Ф ( а,m ) [ A₁].

Задание поверхности на чертеже каркасом или определителем не всегда обеспечивает наглядность ее изображения. В некоторых случаях поверхность целесообразнее задавать ее очерком.

Очерком поверхности называется проекция проецирующей цилиндрической поверхности, огибающей заданную поверхность.

По известному уравнению поверхности или се определителю, или очерку всегда можно построить каркас поверхности.

Многообразие поверхностей требует их систематизации. Для поверхностей, образованных кинематическим способом в основу систематизации положен их определитель.

В зависимости от вида образующей поверхности разделяются на два класса:

Поверхности нелинейчатые

Поверхности нелинейчатые подразделяют на поверхности с образующей переменного вида (изменяющей свою форму в процессе движения) и на поверхности с образующей постоянного вида.

Нелинейчатые поверхности с образующей переменного вида

К нелинейчатым поверхностям с образующей переменного вида относятся:

1. Поверхность общего вида. Такая поверхность образуется перемещением образующей переменного вида а по криволинейной направляющей т (рис. 98).

2. Каналовая поверхность. Эта поверхность образуется движением плоской замкнутой линии, плоскость которой определенным образом ориентирована в пространстве (рис. 99).

Площадь, ограниченная образующей, монотонно изменяется в процессе ее движения но направляющей. Например, каналовую поверхность имеет переходный участок, соединяющий два трубопровода разной формы.

Примером циклической поверхности может быть корпус духового музыкального инструмента.

Нелинейчатые поверхности с образующей постоянного вида

К нелинейчатым поверхностям с образующей постоянного вида относятся:

1. Поверхность общего вида. Такая поверхность может быть образована движением произвольной кривой линии а по направляющей m (рис. 101).

2. Трубчатая поверхность. Образующей трубчатой поверхности является окружность постоянного радиуса. Плоскость окружности при ее движении остается перпендикулярной к направляющей (рис. 102).

Примером трубчатой поверхности может быть поверхность проволоки круглого сечения.

Поверхности линейчатые

Линейчатые поверхности образуются движением прямой (образующей) по заданному закону. В зависимости от закона движения образующей получаем различные линейчатые поверхности.

Линейчатые поверхности с тремя направляющими

К линейчатым поверхностям с тремя направляющими относятся:

1. Поверхность косого цилиндра. Такая поверхность может быть образована движением прямолинейной образующей по трем криволинейным направляющим (рис. 103).

P e ш е н и е. Для определения недостающей проекции точки, воспользуемся признаком принадлежности ее поверхности: точка принадлежит поверхности; если она принадлежит какой-либо линии этой поверхности.

Для данной линейчатой поверхности при построении проекций образующей сначала задается ее горизонтальная проекция, а затем находится фронтальная. Поэтому через известную горизонтальную проекцию точки A’ проводим проекцию образующей а’₂, определяем ее фронтальную проекцию а₂«, на которой по линии связи найдем искомую фронтальную проекцию точки A».

Для определения недостающей горизонтальной проекции точки В’ выполним следующие построения:

1. Построим ряд образующих заданной поверхности a₁,a₂,a₃,a₄ .

2. На фронтальной плоскости проекций через известную проекцию точки В» проведем проекцию вспомогательной линии b’ принадлежащей заданной поверхности и пересекающей образующие.

3. По известным фронтальным проекциям точек пересечения проекции линии b» с образующими а₁«, а₂«, а₃«, а₄« найдем горизонтальные проекции этих точек. Соединив их плавной линией, построим горизонтальную проекцию вспомогательной линии b’ на которой по линии связи найдем искомую проекцию точки В’.

К линейчатым поверхностям с тремя направляющими относятся, например, поверхности гребных винтов судов и пропеллеров самолетов. В архитектуре и строительстве они используются при возведении крытых зданий стадионов, рынков, вокзалов.

Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана)

К линейчатым поверхностями с двумя направляющими плоскостью параллелизма относятся:

a( n ⊥ a) (рис. 108). Поверхность прямого коноида используется в гидротехническом строительстве для формирования поверхности устоев мостовых опор.

Линейчатые поверхности с одной направляющей (торсы)

1. Поверхность с ребром возврата. Эта поверхность образуется движением прямолинейной образующей, во всех своих положениях касательной к пространственной кривой, называемой ребром возврата.

2. Цилиндрическая поверхность. Данная поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и остающейся параллельной своему исходному состоянию (рис.110).

3. Коническая поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и проходящей во всех своих положениях через одну и ту же неподвижную точку S (рис. 111).

Источник