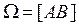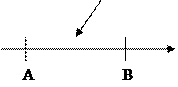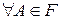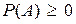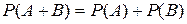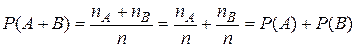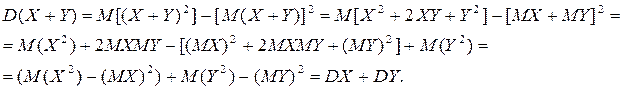Что такое опыт в теории вероятности

Основные понятия теории вероятностей

Что нужно знать

Это самая первая, вводная статья по теории вероятностей. Сама наука является достаточно самостоятельным разделом математики, и, чтобы понять её основы (а также для того, чтобы научиться решать простейшие задачи вроде задания 4 из ЕГЭ), нужно лишь уметь совершать арифметические действия с числами и дробями. Так что, если вам тяжело даются логарифмы и тригонометрия или совершенно непонятна производная, это никак не помешает вам разобраться в теории вероятностей.

Что вы узнаете

Что такое испытание и исход

Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание. Вообще говоря, эксперимент должен быть повторяемым. То есть, чтобы мы могли говорить о вероятности, у нас должна быть возможность провести эксперимент не один (а если совсем строго, то сколько угодно) раз.

Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: <выпало 6 6 6 > и <выпало не 6 6 6 >, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).

На столе лежит колода карт, а мы вытягиваем оттуда одну карту. Это пример случайного испытания. У этого испытания 5 2 52 5 2 исхода, так как мы можем вытянуть любую из 5 2 52 5 2 карт (в каждой из четырех мастей 1 3 13 1 3 карт от двойки до туза).

Бросок обыкновенного игрального кубика является классическим примером испытания. Сколько исходов возможно у этого испытания?

Важно понимать, что список возможных результатов мы очерчиваем сами (исходя из «здравого смысла»). Так, при броске монеты мы считаем «возможным», что она упадёт вверх аверсом («орлом») или вверх реверсом («решкой»), просто не рассматривая возможности того, что монета встанет на ребро, будет проглочена пролетающей птицей и т.п. В то же время мы считаем несущественным, упадёт монета на стол или на пол, со звоном или бесшумно и пр.; мы ограничили себя двумя интересующими нас исходами.

Рассмотрим чуть более сложный пример: мы одновременно подкинули монету и бросили игральный кубик. Сколько (и каких) исходов у этого испытания?

Для ответа на этот вопрос попробуем составить список результатов. Для монеты: Орёл (О) и Решка (Р). Для кубика: 1, 2, 3, 4, 5, 6. А теперь посмотрим, что может быть с кубиком, если монета выпала на Орла? Но ведь кубику в некотором смысле «всё равно», как выпала монета (в теории вероятностей это называется «независимые события», но об этом позже). То есть для него по-прежнему возможны все 6 вариантов. То же самое и если она выпала на Решку. Значит, можно перечислить все возможные исходы подряд, в виде «результат монеты» — «результат кубика». Сделаем это:

Представим следующее испытание: два игральных кубика бросают одновременно. Сколько исходов будет в этом случае?

Что такое случайное событие

Случайное событие — это подмножество множества исходов испытания.

Из скольки исходов состоит случайное событие «выпал дубль» (то есть одинаковые числа на кубиках) при испытании «бросание двух кубиков одновременно»?

Попробуйте ответить на вопрос посложнее:

Из скольки исходов состоит случайное событие «сумма очков на двух кубиках меньше 4»? Испытание то же — два кубика бросают одновременно.

Как считать вероятность события

Исходы, входящие в событие, называются благоприятными для этого события.

Прежде чем перейти к классическому определению вероятности, заметим, что для его применения требуется выполнение определённого условия — равновозможности всех исходов. Это условие может быть недостаточно строго определено, но интуитивно оно понятно. Например, если в качестве исходов при бросании монеты выбрать «орёл», «решка» и «ребро», то классическое определение вероятности применять нельзя, так как шансы на последний исход меньше, чем на первые два. А если выбрать только «орёл» и «решка», то можно — ведь нет никаких оснований считать один исход более частым, чем другой.

Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.
P < Событие A >= Число исходов, благоприятных для A Общее число исходов P\<\text<Событие >A\>=\frac <\text<Число исходов, благоприятных для >A><\text<Общее число исходов>> P < Событие A >= Общее число исходов Число исходов, благоприятных для A ​

Конечно, «в жизни» в основном встречаются ситуации, когда одни исходы встречаются чаще других, и тогда нужно использовать скорректированное определение вероятности. Но в школьных задачах исходы всегда одинаково ожидаемы, так что для нахождения вероятности нужно только правильно посчитать количество исходов, входящих в событие, и общее количество исходов испытания, после чего поделить одно на другое.

Рассмотрим пример. Из стандартной колоды карт (от двойки до туза) наугад вытащили одну карту. Какова вероятность, что эта карта — с цифрой?

Чему равна вероятность достоверного события?

Попробуйте решить несложную задачу, чтобы убедиться, что всё понятно.

В классе 21 человек, среди них 2 Саши. Классный руководитель назначил дежурной Настю и случайным образом выбирает ей напарника. Какова вероятность, что напарником окажется Саша? (Запишите ответ в виде десятичной дроби.)

Эту статью написал для вас Сергей Вальковский, учитель математики Центра образования «Пятьдесят седьмая школа», Москва.

Источник

Вероятностный эксперимент. Предмет и задачи теории вероятностей.

ГЛАВА 1 ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Вероятностный эксперимент. Предмет и задачи теории вероятностей.

Результаты любого эксперимента в той или иной степени зависят от комплекса условий S, при которых данный эксперимент производится. Эти условия либо объективно существуют, либо создаются искусственно (т.е. производится планирование эксперимента).

По степени зависимости результатов эксперимента от условий, при которых он производился, все эксперименты можно разделить на два класса: детерминированные и вероятностные.

o Детерминированные эксперименты—это эксперименты, результаты которых можно предвидеть заранее на основании естественнонаучных законов исходя из данного комплекса условий S.

Примером детерминированного эксперимента является определение ускорения, получаемого телом массы m под воздействием силы F, т.е.. Искомая величина однозначно определяется комплексом условий эксперимента (т.е. массой тела m и силой F).

Детерминированными являются, например, все процессы, основанные на использовании законов классической механики, согласно которым движение тела однозначно определяется заданными начальными условиями и силами, действующими на тело.

o Вероятностные эксперименты (стохастические или случайные)—эксперименты, которые можно повторять произвольное число раз при соблюдении одних и тех же стабильных условий, но, в отличие от детерминированного, исход вероятностного эксперимента неоднозначен, случаен. Т.е. нельзя заранее на основании комплекса условий S предвидеть результат вероятностного эксперимента. Однако, если вероятностный эксперимент повторять многократно при одних и тех же условиях, то совокупность исходов таких экспериментов подчиняется определенным закономерностям. Изучением этих закономерностей (а точнее их математических моделей) и занимается теория вероятностей. Приведем несколько примеров вероятностных экспериментов, которые в дальнейшем будем называть просто экспериментами.

Пример 1

Пусть эксперимент заключается в однократном подбрасывании симметричной монеты. Этот эксперимент может закончиться одним из исключающих друг друга исходов: выпадение герба или решетки (решки). Если точно знать начальные скорости поступательного и вращательного движения и начальное положение монеты в момент броска, то можно предвидеть результат этого эксперимента по законам классической механики. Т.е. он был бы детерминированным. Однако исходные данные эксперимента не могут быть зафиксированными и постоянно изменяются. Поэтому говорят, что результат эксперимента неоднозначен, случаен. Тем не менее, если будем подбрасывать одну и ту же симметричную монету многократно по достаточно длинной траектории, т.е. по возможности сохраним стабильными некоторые условия эксперимента, то совокупное число его исходов подчиняется определенным закономерностям: относительная частота выпадения герба , частоте выпадение бросков (n—число бросков, m₁—число выпадений герба, m₂—решки).

Пример 2

Предположим, что мы заполняем карточку спортлото. До проведения тиража выигрышей невозможно предсказать, сколько номеров будет правильно угадано. Однако опыт проведения тиража спортлото говорит о том, что средний процент игроков, угадавших m (1≤m≤6) номеров, колеблется около некоторой постоянной величины. Эти «закономерности» (средний процент правильного угадывания данного количества номеров) используются для расчета фондов выигрыша.

Вероятностные эксперименты имеют следующие общие черты: непредвиденность результата; наличие определенных количественных закономерностей при их многократном повторении при одинаковых условиях; множество возможных исходов.

o Предметом теории вероятностейявляется количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статической обработкой экспериментальных данных.

o Теория вероятностей—наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.

События и операции над ними.

Относительные частоты и их свойства

Первичным понятием теории вероятностей, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.

Пример

1. Предположим, что бросается симметричная монета. Тогда (герб и решка).

2. Игральная кость .

3. Бросаются две монеты .

4. Бросаются две игральных кости . Число элементарных исходов 36.

5. На [AB] числовой оси w бросается наудачу точка.

6. На [AB] бросаются две точки .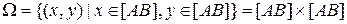

y

Определение. Событиемназывается произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А.

Говорят, что событие А произошло, если в результате эксперимента происходит элементарный исход w 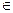A, т.е. благоприятствующий событию А.

Рассмотрим пример 2. , –событие, состоящее в выпадении нечетного числа очков; –событие, состоящее в выпадении четного числа очков.

o Все пространство элементарных исходов Ω, если взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).

o Пустое множество (т.е. множество, которое не содержит ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не происходит.

Все остальные события, кроме Ω и , называются случайными.

Операции над событиями

0.1Суммой событий А и В называется объединение этих множеств А B.

или .

–событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.

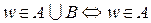
0.2Произведением событий А и В называется пересечение множеств А и В, т.е. А В. Обозначается как АВ.

АВ–событие, когда А и В происходят одновременно.

и .

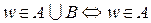
0.3Разностью событий А и В называется разность множеств А\В.

и .

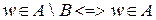
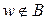
o События А и В называются несовместимыми, если 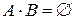. Если А и В несовместимы, то будем обозначать .

o Говорят, что событие А влечет событие В, если А является подмножеством В, т.е. 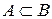(когда происходит А, происходит В).

.

o Событие называется противоположным к событию А.

Пример 2. . происходит тогда, когда А не происходит.

o Говорят, что события Н₁,Н₂,…,Н_n образуют полную группу, если Н₁+Н₂+…+Н_n=Ω (т.е. Н₁, Н₂, Н_n–несовместимы, т.е. Н_i Н_j= , если i≠j).

Например, А и образуют полную группу: .

Предположим, что производится некоторый случайный эксперимент, результат которого описывается пространством Ω. Произведем N экспериментов. Пусть А—некоторое событие ( 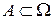), N(A)—число тех экспериментов, в которых произошло событие А.

Тогда число называется относительной частотой события А.

Аксиомы теории вероятностей

Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.

o Событие—это подмножество Ω, принадлежащее классу F. Любому ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы:

Аксиома 1.

Аксиома 2. ,т.е. вероятность достоверного события равна 1.

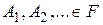
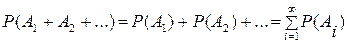
Аксиома 3.(счетной аддитивности) Если и , то (для несовместимых событий).

Элементы комбинаторики

Лемма 1. Из m элементов а₁,…,а_m первой группы и n элементов b₁,…,b_n второй группы можно составить ровно m∙n упорядоченных пар вида (а_i, b_j), содержащих по одному элементу из каждой группы.

Доказательство:

Всего имеем m∙n пар.

Пример. В колоде 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт. Итого n=4∙9=36.

можно составить ровно n₁∙ n₂∙…∙n_k различных упорядоченных комбинаций вида , содержащих по одному элементу из каждой группы.

1. При k=2 утверждение выполняется (Лемма 1).

2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов . Рассмотрим комбинацию как и . Предположение дает возможность вычислить число комбинаций из k элементов, их n₁ n₂ n_k. По Лемме 1 число комбинаций из k+1 элементов n₁ n₂… n_k+1.

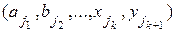
Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216.

Геометрические вероятности

Предположим, что на числовой оси имеется некоторый отрезок [a,b] и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на .

—геометрическая вероятность на прямой.

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:

—геометрическая вероятность на плоскости.

Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством:

—геометрическая вероятность в пространстве.

Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности.

Свойства вероятности

Свойство 1.Вероятность невозможного события равна 0, т.е. . .

Свойство 2.Вероятность достоверного события равна 1, т.е. , .

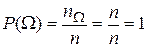
Свойство 3.Для любого события . , т.к. , то и следовательно .

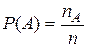
Свойство 4.Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:

Случайные величины

o Случайной величиной Хназывается функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.

Пример. Пусть дважды подбрасывается монета. Тогда .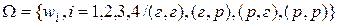

Рассмотрим случайную величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0.

Множество значений случайной величины обозначается Ω_х. Одной из важных характеристик случайной величины является функция распределения случайной величины.

o Функцией распределения случайной величины Хназывается функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.

.

.

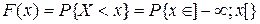
Если рассматривать Х как случайную точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.

Простейший поток событий.

Рассмотрим события, которые наступают в случайные моменты времени.

o Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.

Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие.

Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последствия и ординарности.

o Поток событий называется стационарным, если вероятность появления k событий за промежуток времени длительности t зависит только от k и t.

Таким образом, свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени (1, 7), (10, 16), (Т, Т+6) одинаковой длительности t=6 единиц времени равны между собой.

o Поток событий называется ординарным,если за бесконечно малый промежуток времени может появиться не более одного события.

Таким образом, свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события в один и тот же момент времени практически равна нулю.

o Говорят, что поток событий обладает свойством отсутствия последствия, если имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени. Таким образом, свойство отсутствия последствия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, условная вероятность появления k событий на любом промежутке времени, вычисленная при произвольном предположении о том, что происходило до начала рассматриваемого промежутка (т.е. сколько событий появилось, в какой последовательности), равна безусловной вероятности. Следовательно, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.

o Поток событий называется простейшим или пуассоновским, если он стационарный, ординарный, без последствия.

o Интенсивностью потока λназывают среднее число событий, которые появляются в единицу времени.

Если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за промежуток времени длительности t определяется по формуле:

, . Формула Пуассона.

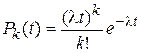
Эта формула отражает все свойства простейшего потока, поэтому ее можно считать математической моделью простейшего потока.

Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.

По условию λ=2, t=5, k=2. По формуле Пуассона

А) —это событие практически невозможно.

Б) —событие практически невозможно, т.к. события «не поступило ни одного вызова» и «поступил один вызов»­­—несовместимы.

В) —это событие практически достоверно.

Свойства дисперсии.

Свойство 1.Дисперсия постоянной величины С равна 0.DC=0.

.

Свойство 2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

.

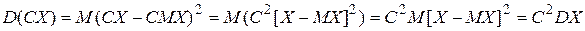
Свойство 3.Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

.

Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.

Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: .

Случайная величина Х—число появлений события А в n независимых испытаниях. , где Х_i—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.

.

. Т.к. MX₁=p. , то . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда .

Пример. Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X—числа появлений события в этих испытаниях.

.

o Начальным моментом порядка к случайным величинам Хназывают математическое ожидание случайной величины Х k :

. В частности, , .

Пользуясь этими моментами, формулу для вычисления дисперсии можно записать так: .

Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х-ХМ.

. В частности

, . Следовательно, .

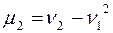
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:

.

.

Моменты более высоких порядков применяются редко.

Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.

Системы случайных величин.

o Вектор , где —случайные величины, называются n-мерным случайным вектором.

o Функция

называется функцией распределения случайного вектора или совместной функцией распределения случайных величин .

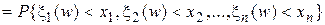
Свойство 4.

.

= .

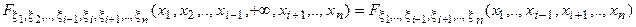
o Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины.

o Случайный вектор 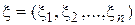называется непрерывным, если существует неотрицательная функция , называется плотностью распределения случайных величин такая, что функция распределения .

Свойства корреляции.

Свойство 1.Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. .

Свойство 2.Для того чтобы 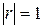необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. с вероятностью 1.

Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0.

Пусть Х и Y—независимы, тогда по свойству математического ожидания

o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.

o Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0.

Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости.

o Коэффициентом асимметрии случайной величины Х называется число

Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.

o Эксцессом случайной величины Х называется число .

Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.

Производящие функции

o Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,…

Таким образом, если случайная величина Х—целочисленная, то она имеет ряд распределения

o Пусть Х—целочисленная величина с законом распределения

Ее производящей функцией называется функция

Распределение «xи квадрат»

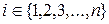
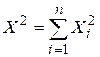
Пусть X_i, —нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин распределена по закону Х 2 с k=n степенями свободы. Если же эти величины Х_i связаны одним линейным соотношением, например , то число степеней свободы k=n-1.

Плотность этого распределения , где —гамма-функция; в частности, Г(n+1)=n!

Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Распределение Стьюдента

Пусть Z—нормально распределенная величина, причем M(Z)=0, G 2 =1, т.е. Z

N(0,1), а V—независимая от Z величина, которая распределена по закону Х 2 с k степенями свободы. Тогда величина имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Плотность распределения случайной величины t имеет вид , .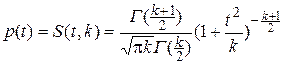

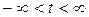
Случайная величина t имеет математическое ожидание Mt=0, (k>2).

Распределение Фишера

Если U и V—независимые случайные величины, распределенные по закону Х 2 со степенями свободы k₁ и k₂, то величина 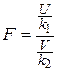имеет распределение Фишера F со степенями свободы k₁ и k₂. Плотность этого распределения , где

.

Распределение Фишера F определяется двумя параметрами—числами степеней свободы.

Характеристические функции

0. 1Случайная величина , где i—мнимая единица, т.е. ,а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной. (i 2 = –1).

0. 2Математическим ожиданием комплекснозначной случайной величины Z называется 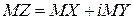. Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин.

0. 3Комплекснозначные случайные величины Z₁=X₁+iY₁ и Z₂=X₂+iY₂ называются независимыми, если независимы соответственно .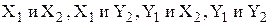

Законы больших чисел

0. 1Последовательность случайных величин Х₁, Х₂,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа , т.е.

при . Обозначается .

0. 2 Говорят, что последовательность случайных величин Х₁, Х₂,… удовлетворяют закону больших чисел, если .

Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство Чебышёва:

Для . .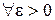

.

Таким образом,

.

Теорема 2. (закон больших чисел в форме Чебышёва).

Пусть Х₁,Х₂,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. . Тогда эта последовательность удовлетворяет закону больших чисел.

Обозначим через . Нужно доказать, что .

.

Отсюда (т.к. ).

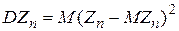
Случайные функции

o Случайной функциейназывается функция X(t), значение которой при любом значении аргумента t является случайной величиной.

Другими словами, случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, при этом заранее не известно, какой именно.

o Конкретный вид, принимаемый случайной величиной в результате опыта, называется реализацией случайной функции.

Т.к. на практике аргумент t чаще всего является временным, то случайную функцию иначе называют случайным процессом.

На рисунке изображено несколько реализаций некоторого случайного процесса.

Если зафиксировать значение аргумента t, то случайная функция X(t) превратится в случайную величину, которую называют сечением случайной функции, соответствующим моменту времени t. Будем считать распределение сечения непрерывным. Тогда Х(t) при данном t определяется плотностью распределения p(x; t).

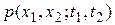
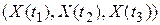
Очевидно, p(x; t) не является исчерпывающей характеристикой случайной функции X(t), поскольку она не выражает зависимости между сечениями X(t) в разные моменты времени t. Более полную характеристику дает функция —совместная плотность распределения системы случайных величин , где t₁ и t₂—произвольные значения аргумента t случайной функции. Еще более полную характеристику случайной функции X(t) даст совместимая плотность распределения системы трех случайных величин и т.д.

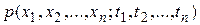
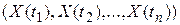
o Говорят, что случайный процесс имеет порядок n, если он полностью определяется плотностью совместимого распределения n произвольных сечений процесса, т.е. системы n случайных величин , где X(t_i)—сечение процесса, отвечающее моменту времени t_i, но не определяется заданием совместного распределения меньшего, чем n, числа сечений.

o Если плотность совместного распределения произвольных двух сечений процесса вполне его определяет, то такой процесс называется марковским.

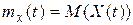
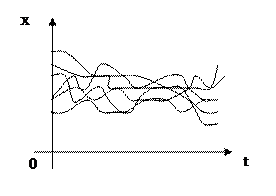
Пусть имеется случайная функция X(t). Возникает задача описания ее с помощью одной или нескольких неслучайных характеристик. В качестве первой из них естественно взять функцию —математическое ожидание случайного процесса. В качестве второй берется среднее квадратическое отклонение случайного процесса .

Эти характеристики являются некоторыми функциями от t. Первая из них—это средняя траектория для всех возможных реализаций. Вторая характеризует возможный разброс реализаций случайной функции около средней траектории. Но и этих характеристик недостаточно. Важно знать зависимость величин X(t₁) и X(t₂). Эту зависимость можно характеризовать с помощью корреляционной функции или корреляционного момента.

. (1)

Пусть имеются два случайных процесса, по нескольку реализаций которых изображено на рисунках.

У этих случайных процессов примерно одинаковые математические ожидания и средние квадратичные отклонения. Тем не менее это различные процессы. Всякая реализация для случайной функции X₁(t) медленно меняет свои значения с изменением t, чего нельзя сказать о случайной функции X₂(t). У первого процесса зависимость между сечениями X₁(t) и 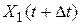будет больше, чем зависимость для сечений X₂(t) и второго процесса, т.е. убывает медленнее, чем , при увеличении Δt. Во втором случае процесс быстрее «забывает» свое прошлое.

Остановимся на свойствах корреляционной функции, которые вытекают из свойств корреляционного момента пары случайных величин.

Свойство 1.Свойство симметричности .

Свойство 2.Если к случайной функции X(t) прибавить неслучайное слагаемое , то от этого корреляционная функция не изменится, т.е. .

Источник