Что такое ордината и абсцисса в алгебре
Обычно абсцисса относится к горизонтальной оси ( x ), а ордината относится к вертикальной оси ( y ) стандартного двухмерного графика.
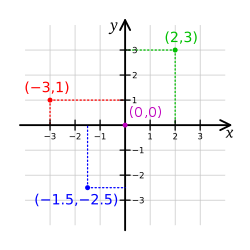
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
СОДЕРЖАНИЕ
Этимология
В своей работе 1892 года « Vorlesungen über die Geschichte der Mathematik» (« Лекции по истории математики »), том 2, немецкий историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht Kommt Дас Сусло в Uebersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
Обычно абсцисса относится к горизонтальной оси ( x ), а ордината относится к вертикальной оси ( y ) стандартного двухмерного графика.
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
СОДЕРЖАНИЕ
Этимология
В своей работе 1892 года « Vorlesungen über die Geschichte der Mathematik» (« Лекции по истории математики »), том 2, немецкий историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht Kommt Дас Сусло в Uebersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
Абсцисса (математика)
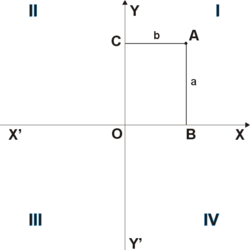
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рис. 1). Если точка B принадлежит положительной полуоси OX, то абсцисса имеет положительное значение. Если точка B принадлежит отрицательной полуоси X’O, то абсцисса имеет отрицательное значение. Если точка A лежит на оси Y’Y, то её абсцисса равна нулю.
В прямоугольной системе координат ось X’X называется «осью абсцисс».
При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Правописание
Обратите внимание на написание: Абсцисса, но не абцисса и не абсциса.
См. также
Смотреть что такое «Абсцисса (математика)» в других словарях:
АБСЦИССА — (от лат. abscindere отрезывать, отделять, отрывать). 1) пространство между ординатой и точкой, положение которой определяют на плоскости. 2) отрезок. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АБСЦИССА одна из … Словарь иностранных слов русского языка
Лейбниц, Готфрид Вильгельм — Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
НАУКА — особый вид познавательной деятельности, направленный на выработку объективных, системно организованных и обоснованных знаний о мире. Взаимодействует с др. видами познавательной деятельности: обыденным, художественным, религиозным, мифологическим … Философская энциклопедия
Аналитическая геометрия — Декартова система координат Аналитическая геометрия раздел геометрии, в котором … Википедия
Аполлоний Пергский — У этого термина существуют и другие значения, см. Аполлоний. Аполлоний Пергский Дата рождения: 262 год до н. э.( 262) Место рождения: Перге, Памфилия Дата смерти … Википедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
Математическая формула — Эта статья об обозначениях элементарной математики; Для более общего контекста см.: Математические обозначения. Математическая формула (от лат. formula уменьшительное от forma образ, вид) принятая в математике (а также… … Википедия
Полярная система координат — Полярная сетка, на которой отложено несколько углов с пометками в градусах. Полярная система координат двумерная система координат, в которой каждая точка на плоскости определяется двумя числами полярным углом и полярны … Википедия
Лейбниц Готфрид Вильгельм — (Leibniz) (1646 1716), немецкий философ, математик, физик, языковед. С 1676 на службе у ганноверских герцогов. Основатель и президент (с 1700) Бранденбургского научного общества (позднее Берлинская АН). По просьбе Петра I разработал проекты… … Энциклопедический словарь
Абсцисса и ордината
Обычно абсцисса относится к горизонтальной оси ( x ), а ордината относится к вертикальной оси ( y ) стандартного двухмерного графика.
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
В своей работе 1892 года « Vorlesungen über die Geschichte der Mathematik» (« Лекции по истории математики »), том 2, немецкий историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt wordden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht Kommt Дас Сусло в Uebersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte. [2]
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
Ось ординат

Всего получено оценок: 128.
Всего получено оценок: 128.
Оси абсцисс и ось ординат – это вечная проблема, как учеников, так и студентов. Названия осей по переменным х и у запоминаются куда легче, поэтому все привыкли использовать их. Почему нужно знать изначальные названия и откуда взялось понятие ординаты расскажем ниже.
Декартова система координат
Рене Декарт прославился многими открытиями в науке, несмотря на всяческие гонения со стороны бушевавшей инквизиции. Но в умах многих и многих поколений потомков он остался как изобретатель декартовой или прямоугольной системы координат.
Прямоугольная система координат сегодня используется везде: в радарах, для настройки светового оборудования, в оптике – практически любая отрасль не может обойтись без использования столь удобной системы.
Система Декарта состоит из двух взаимно перпендикулярных прямых. В любой системе координат обязательно должны быть:
Единичные отрезки на разных осях могут быть различны. Размер отрезка выбирают в соответствии с отметками, которые нужно нанести.
Оси координат
Оси координат это основа системы. Чтобы узнать координаты какой-либо точки, нужно опустить перпендикуляры на каждую из осей. Отрезки, заключенные между точкой отчета и точкой пересечения оси с перпендикуляром зовутся проекциями точки на оси. Размер этих проекций, выраженный в единичных отрезках, и есть координаты точки.
Традиционно оси называют переменными х и у. Это связано с традиционной записью функций, которые часто в виде графиков переносятся на ось координат. Например, функция у=х+3 – прямая линия. При этом сразу понятно, что если подставить любое число вместо х, то можно получить соответствующее значение у. Так высчитывают координаты точки в составе графика.
По факту оси можно называть как угодно. Это зависит только от ученика, решающего задачу. А названия абсцисс и ординат сохраняется всегда.
Осью абсцисс зовется ось х. Она отвечает за отслеживание горизонтальных перемещений точки. В переводе с латинского языка «абсцисса» переводится как «отрезок».
Если говорить кратко о оси ординат, то так зовется ось у. Эта ось отвечает за перемещения по вертикали. Если точка поднимается или опускается, это можно отследить по изменению ординаты. Ордината переводится как порядок.
Осью абсцисс зовется ось х. Она отвечает за отслеживание горизонтальных перемещений точки. В переводе с латинского языка «абсцисса» переводится как «отрезок».
Если воспользоваться переводом, то можно сказать так: чтобы отметить точку в системе координат, нужно отложить отрезок по горизонтали, равный абсциссе и поднять точку на несколько порядков вверх по ординате. Так проще запомнить правильные названия осей.
Что мы узнали?
Мы поговорили о Декартовой системе координат. Узнали, зачем нужно использовать правильные названия осей. Поговорили о том, что такое абсцисса и ордината. Выяснили, почему чаще всего оси обозначаются х и у. Сказали о том, что традиционное обозначение может быть заменено в любой момент.