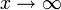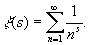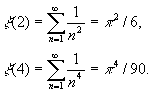Что такое дзета функция
Римана дзета-функция
Дзета-функция Римана ζ(s) определяется с помощью ряда Дирихле:
.
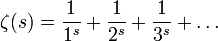
В области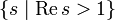 
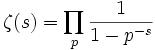
, этот ряд сходится, является аналитической функцией и допускает аналитическое продолжение на всю комплексную плоскость без единицы. В этой области также верно представление в виде бесконечного произведения (тождество Эйлера)
,
Содержание
Свойства
Нули дзета-функции
История
Как функция вещественной переменной, дзета-функция была введена в 1737 году Эйлером, который и указал её разложение в произведение. Затем эта функция рассматривалась Дирихле и, особенно успешно, Чебышёвым при изучении закона распределения простых чисел. Однако наиболее глубокие свойства дзета-функции были обнаружены позднее, после работы Римана (1859), где дзета-функция рассматривалась как функция комплексной переменной.
Ссылки
Полезное
Смотреть что такое «Римана дзета-функция» в других словарях:
РИМАНА ДЗЕТА-ФУНКЦИЯ — см.Дзета функция … Математическая энциклопедия
Римана дзета-функция — (математическая) см. Дзета функция … Большая советская энциклопедия
ДЗЕТА-ФУНКЦИЯ — z ф у нкция, 1) Д. ф. в теории чисел класс аналитич. функций комплексного переменного, состоящий из z функции Римана, ее обобщений и аналогов. Д. ф. и их обобщения в виде L функций (см. Дирихле L функции )лежат в основе современной аналитич.… … Математическая энциклопедия
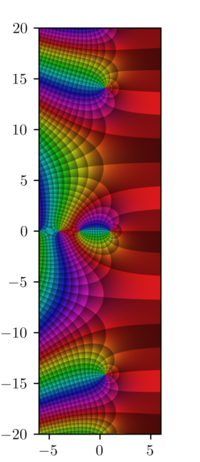
Дзета-функция Римана — Запрос «Дзета функция» перенаправляется сюда; см. также другие значения. Качественный график дзета функции Римана на действительной оси. Слева от нуля значения функции увеличены в 100 раз … Википедия
Дзета-функция Гурвица — В математике Дзета функция Гурвица, названная в честь Адольфа Гурвица, это одна из многочисленных дзета функций, являющихся обобщениями дзета функции Римана. Формально она может быть определена степенным рядом для комплексных аргументов s,… … Википедия
Дзета-функция — 1) аналитическая функция комплексного переменного s = σ + it, определяемая при σ > 1 формулой Эту функцию для действительных s ввёл в математический анализ Л. Эйлер (1737), а для комплексных s впервые изучал немецкий… … Большая советская энциклопедия
Дзета-функции — Эта страница информационный список. См. также основную статью: Дзета функция Римана В математике дзета функция обычно это функция родственная или аналогичная дзета функции Римана … Википедия
Функция Мертенса — В теории чисел, функция Мертенса определяется для всех натуральных чисел n формулой где функция Мёбиуса. Функция Мертенса названа в честь Франца Мертенса. Другими словами, это разность между количеством свободных от квадратов чисел, не… … Википедия
ФУНКЦИЯ — термин, используемый в математике для обозначения такой зависимости между двумя величинами, при которой если одна величина задана, то другая может быть найдена. Обычно функция (с 17 в.) задается формулой, выражающей зависимую переменную через… … Энциклопедия Кольера
СОДЕРЖАНИЕ
Определение
Конкретные значения
Для любого положительного четного числа 2 n :
Для неположительных целых чисел
В частности, ζ обращается в нуль при отрицательных четных целых числах, потому что B m = 0 для всех нечетных m, кроме 1. Это так называемые «тривиальные нули» дзета-функции.
С помощью аналитического продолжения можно показать, что:
Формула произведения Эйлера
В 1737 году связь между дзета-функцией и простыми числами была обнаружена Эйлером, который доказал тождество
Функциональное уравнение Римана
Для удобства пусть
так что 2 ψ ( Икс ) + 1 знак равно 1 Икс < 2 ψ ( 1 Икс ) + 1 >. <\ displaystyle 2 \ psi (x) + 1 = <1 \ over <\ sqrt 
Функциональное уравнение было установлено Риманом в его статье 1859 года « О числе простых чисел меньше заданной величины » и использовалось, в первую очередь, для построения аналитического продолжения. Эквивалентное соотношение было предположено Эйлером более ста лет назад, в 1749 году, для эта-функции Дирихле (переменной дзета-функции):
Риман также нашел симметричную версию функционального уравнения, применимого к xi-функции:
Нули, критическая линия и гипотеза Римана
| Нуль |
|---|
| 1/2 ± 14,134725 и |
| 1/2 ± 21,022040 я |
| 1/2 ± 25,0 · 10858 я |
| 1/2 ± 30,424876 и |
| 1/2 ± 32,93 5062 и |
| 1/2 ± 37,586178 я |
Количество нулей в критической полосе
Гипотезы Харди – Литтлвуда
В 1914 году Годфри Гарольд Харди доказал, что ζ ( 1 / 2 + it ) имеет бесконечно много действительных нулей.
Эти две гипотезы открыли новые направления в исследовании дзета-функции Римана.
Нулевой регион
В 2015 году Моссингхофф и Трудгиан доказали, что дзета не имеет нулей в этом регионе.
Другие результаты
Известно, что на критической прямой бесконечно много нулей. Литтлвуд показал, что если последовательность ( γ n ) содержит мнимые части всех нулей в верхней полуплоскости в порядке возрастания, то
Теорема о критической прямой утверждает, что положительная доля нетривиальных нулей лежит на критической прямой. (Гипотеза Римана подразумевает, что эта пропорция равна 1.)
ζ ( s ) знак равно ζ ( s ¯ ) ¯ <\ displaystyle \ zeta (s) = <\ overline <\ zeta (<\ overline >)>>>
Различные свойства
Взаимный
Обратная величина дзета-функции может быть выражена в виде ряда Дирихле по функции Мёбиуса μ ( n ) :
Универсальность
Оценки максимума модуля дзета-функции
Пусть функции F ( T ; H ) и G ( s 0 ; Δ) определены равенствами
Анатолий Карацуба доказал, в частности, что если значения H и Δ превосходят некоторые достаточно малые константы, то оценки
Аргумент дзета-функции Римана
содержит как минимум
точки, в которых функция S ( t ) меняет знак. Ранее аналогичные результаты были получены Атле Сельбергом для случая
Представления
Серия Дирихле
Расширение области сходимости можно получить, переставив исходный ряд. Сериал
Интегралы типа Меллина
Преобразование Меллина функции f ( x ) определяется как
в области определения интеграла. Существуют различные выражения для дзета-функции в виде интегралов, подобных преобразованию Меллина. Если действительная часть s больше единицы, мы имеем
для всех s (где H обозначает контур Ганкеля ).
Тета-функции
Дзета-функция Римана может быть задана преобразованием Меллина
Однако этот интеграл сходится только в том случае, если действительная часть s больше 1, но его можно регуляризовать. Это дает следующее выражение для дзета-функции, которое хорошо определено для всех s, кроме 0 и 1:
Серия Laurent
Константы γ n здесь называются константами Стилтьеса и могут быть определены пределом
интеграл
верно, что может быть использовано для численной оценки дзета-функции.
Растущий факториал
Это можно использовать рекурсивно, чтобы расширить определение ряда Дирихле на все комплексные числа.
Произведение Адамара
Глобально сходящийся ряд
Серия появилась в приложении к статье Хассе и была опубликована во второй раз Джонатаном Сондоу в 1994 году.
Хассе также доказал глобально сходящийся ряд
в той же публикации. Исследование Ярослава Благушина показало, что аналогичная эквивалентная серия была опубликована Йозефом Сером в 1926 году.
Представление ряда в натуральных числах через примитив
Представление ряда неполными полибернулли-числами
Функция ζ может быть представлена при Re ( s )> 1 бесконечным рядом
Преобразование Меллина карты Энгеля
Представление ряда в виде суммы геометрического ряда
По аналогии с произведением Эйлера, которое может быть доказано с помощью геометрических рядов, дзета-функция для Re ( s )> 1 может быть представлена в виде суммы геометрических рядов:
Численные алгоритмы
Классический алгоритм, использовавшийся примерно до 1930 г., основан на применении формулы Эйлера-Маклорена для получения для n и m положительных целых чисел
и ошибка удовлетворяет
Приложения
Бесконечная серия
Дзета-функция, вычисленная на эквидистантных положительных целых числах, появляется в бесконечных последовательностях представлений ряда констант.
Фактически, четный и нечетный члены дают две суммы
Параметризованные версии приведенных выше сумм даются формулами
где Im обозначает мнимую часть комплексного числа.
Еще больше формул можно найти в статье Число гармоник.
Обобщения
Существует ряд связанных дзета-функций, которые можно рассматривать как обобщения дзета-функции Римана. К ним относятся дзета-функция Гурвица
что совпадает с дзета-функцией Римана при z = 1 и q = 1 (нижний предел суммирования в трансценденте Лерха равен 0, а не 1).
Эти функции можно аналитически продолжить на n- мерное комплексное пространство. Специальные значения, принимаемые этими функциями при положительных целочисленных аргументах, теоретиками чисел называются множественными дзета-значениями и связаны со многими различными разделами математики и физики.
Нули дзета-функции Римана
Нули дзета-функции Римана
| Задачи тысячелетия |
|---|
| Равенство классов P и NP |
| Гипотеза Ходжа |
| Гипотеза Пуанкаре |
| Гипотеза Римана |
| Квантовая теория Янга — Миллса |
| Существование и гладкость решений уравнений Навье — Стокса |
| Гипотеза Берча и Свиннертона — Дайера |
Гипо́теза Ри́мана о распределении нулей дзета-функции Римана была сформулирована Бернхардом Риманом в 1859 году.
Функция ζ(s) определена для всех комплексных 
, и имеет нули для отрицательных целых 
. Из функционального уравнения 
, и явного выражения 
при 
следует, что все остальные нули, называемые «нетривиальными», расположены в полосе 
симметрично относительно так называемой «критической линии» 
. Гипотеза Римана утверждает, что:
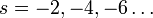
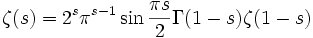
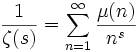
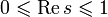
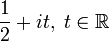
Все нетривиальные нули дзета-функции имеют действительную часть, равную
Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, называемых L-функциями Дирихле.
На 2004 год проверены более 10 13 первых нулей. [1]
Большинство математиков верят, что гипотеза верна. Многие утверждения о распределении простых чисел, в том числе о сложности некоторых целочисленных алгоритмов, доказаны в предположении верности гипотезы Римана. В то время как не существует простой закономерности, описывающей распределение простых чисел среди натуральных, Риман обнаружил, что число π(x) простых чисел, не превосходящих x, выражается через распределение нетривиальных нулей дзета-функции.
Гипотеза Римана входит в список семи «проблем тысячелетия», за решение каждой из которых Математический институт Клэя (Clay Mathematics Institute, Кембридж, Массачусетс) выплатит приз в 1 млн. долларов США. Интересно, что опровержение гипотезы Римана не даст права на получение приза. [1]
Содержание
История
В 1896 Адамар и Валле-Пуссен независимо доказали, что нули дзета-функции не могут лежать на прямых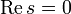 
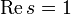
и 
.
В 1900 Давид Гильберт включил гипотезу Римана в список 23 нерешённых проблем как часть восьмой проблемы, совместно с гипотезой Гольдбаха.
В 1914 Харди доказал, что на критической линии находится бесконечно много нулей, а позже Харди и Литлвуд дали оценку снизу доли нулей, лежащей на критической линии, которую потом улучшали разные математики.
Некоторые нетривиальные нули располагаются экстремально близко друг к другу. Это свойство известно как «явление Лемера (Lehmer)».
Титчмарш, Ворос в 1987 показали, что дзета-функция может быть разложена в произведение через свои нетривиальные нули в разложение Адамара.
Группа математиков Университета Пардье (Purdue University, USA) под руководством Луи де Бранжа (Louis De Branges de Bourcia) предложила доказательство гипотезы Римана [2], которое, однако, оказалось неверным [3].
Эквивалентные формулировки
В 1901 Хельге фон Кох показал, что гипотеза Римана эквивалентна следующему утверждению о распределении простых чисел:
при 
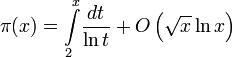
Интересные факты
Знаменит ответ Гильберта на вопрос о том, каковы будут его действия, если он по какой-либо причине проспит пятьсот лет и вдруг проснется. Математик ответил, что самым первым делом он спросит была ли доказана гипотеза Римана.
Примечания
Ссылки
См. также
Полезное
Смотреть что такое «Нули дзета-функции Римана» в других словарях:
Дзета-функция Римана — Запрос «Дзета функция» перенаправляется сюда; см. также другие значения. Качественный график дзета функции Римана на действительной оси. Слева от нуля значения функции увеличены в 100 раз … Википедия
ДЗЕТА-ФУНКЦИЯ — z ф у нкция, 1) Д. ф. в теории чисел класс аналитич. функций комплексного переменного, состоящий из z функции Римана, ее обобщений и аналогов. Д. ф. и их обобщения в виде L функций (см. Дирихле L функции )лежат в основе современной аналитич.… … Математическая энциклопедия
РИМАНА ГИПОТЕЗЫ — в а н а л и т и ч е с к о й т е о р и и ч и с е л пять гипотез, высказанных Б. Риманом (В. Riemann, 1876) относительно распределения нетривиальных нулей дзета функции и относительно выражения через эти нули числа простых чисел, не превосходящих… … Математическая энциклопедия
Дзета-функция — 1) аналитическая функция комплексного переменного s = σ + it, определяемая при σ > 1 формулой Эту функцию для действительных s ввёл в математический анализ Л. Эйлер (1737), а для комплексных s впервые изучал немецкий… … Большая советская энциклопедия
Гипотеза Римана — Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга Миллса Существование и гладкость решений уравнений Навье Стокса Гипотеза Бёрча Свиннертон Дайера Гипотеза Римана о… … Википедия
Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции … Википедия
Сельберг, Атле — Атле Сельберг норв. Atle Selberg … Википедия
Дзета-функция
Полезное
Смотреть что такое «Дзета-функция» в других словарях:
дзета-функция — дзета функция, дзета функции … Орфографический словарь-справочник
ДЗЕТА-ФУНКЦИЯ — z ф у нкция, 1) Д. ф. в теории чисел класс аналитич. функций комплексного переменного, состоящий из z функции Римана, ее обобщений и аналогов. Д. ф. и их обобщения в виде L функций (см. Дирихле L функции )лежат в основе современной аналитич.… … Математическая энциклопедия
дзета-функция — дз ета ф ункция, и … Русский орфографический словарь
дзета-функция — дзе/та фу/нкция, дзе/та фу/нкции … Слитно. Раздельно. Через дефис.
дзета-функция — дзет/а/ функци/я [й/а] … Морфемно-орфографический словарь
Дзета-функция Римана — Запрос «Дзета функция» перенаправляется сюда; см. также другие значения. Качественный график дзета функции Римана на действительной оси. Слева от нуля значения функции увеличены в 100 раз … Википедия
Дзета-функция Гурвица — В математике Дзета функция Гурвица, названная в честь Адольфа Гурвица, это одна из многочисленных дзета функций, являющихся обобщениями дзета функции Римана. Формально она может быть определена степенным рядом для комплексных аргументов s,… … Википедия
Римана дзета-функция — (математическая) см. Дзета функция … Большая советская энциклопедия
Гипотеза Римана
Содержание
Дзета-функция Римана [ править ]
В полосе 0 дзета-функция удовлетворяет функциональному уравнению
Затем можно определить ζ ( s ) для всех оставшихся ненулевых комплексных чисел s ( Re ( s ) ≤ 0 и s 0), применив это уравнение вне полосы и положив ζ ( s ) равным правой части уравнения всякий раз, когда s имеет неположительную действительную часть (и s 0).
Значение ζ (0) = −1/2 не определяется функциональным уравнением, но является предельным значением ζ ( s ), когда s приближается к нулю. Функциональное уравнение также подразумевает, что дзета-функция не имеет нулей с отрицательной действительной частью, кроме тривиальных нулей, поэтому все нетривиальные нули лежат в критической полосе, где s имеет действительную часть между 0 и 1.
Происхождение [ править ]
. es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre Allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien.
. очень вероятно, что все корни настоящие. Конечно, здесь хотелось бы получить строгое доказательство; Я на время, после нескольких мимолетных тщетных попыток, временно отложил поиски этого, поскольку это кажется ненужным для непосредственной цели моего расследования.
Π ( x ) = π ( x ) + 1 2 π ( x 1 2 ) + 1 3 π ( x 1 3 ) + 1 4 π ( x 1 4 ) + 1 5 π ( x 1 5 ) + 1 6 π ( x 1 6 ) + ⋯ <\displaystyle \Pi (x)=\pi (x)+<\tfrac <1><2>>\pi (x^<\frac <1><2>>)+<\tfrac <1><3>>\pi (x^<\frac <1><3>>)+<\tfrac <1><4>>\pi (x^<\frac <1><4>>)+<\tfrac <1><5>>\pi (x^<\frac <1><5>>)+<\tfrac <1><6>>\pi (x^<\frac <1><6>>)+\cdots >
где сумма берется по нетривиальным нулям дзета-функции и где Π 0 представляет собой слегка измененную версию, которая заменяет его значение в точках разрыва на среднее значение его верхнего и нижнего пределов:
Последствия [ править ]
Практическое использование гипотезы Римана включает в себя множество утверждений, известных как истинные в рамках гипотезы Римана, и некоторые из них, которые можно показать как эквивалентные гипотезе Римана.
Распределение простых чисел [ править ]
Явная формула Римана для количества простых чисел меньше заданного числа в терминах суммы по нулям дзета-функции Римана говорит, что величина колебаний простых чисел вокруг их ожидаемого положения контролируется действительными частями нулей дзета-функция. В частности, член ошибки в теореме о простых числах тесно связан с положением нулей. Например, если β является верхней границей вещественных частей нулей, то ( Инги 1932 ) : теорема 30, с.83 ( Montgomery & Vaughan 2007 ) : стр. 430
Уже известно, что 1/2 ≤ β ≤ 1 ( Ingham 1932 ). : p. 82
Шенфельд (1976) также показал, что гипотеза Римана подразумевает
.
Рост арифметических функций [ править ]
Гипотеза Римана подразумевает строгие ограничения на рост многих других арифметических функций в дополнение к функции подсчета простых чисел выше.
Один из примеров включает функцию Мёбиуса μ. Утверждение, что уравнение
1 ζ ( s ) = ∑ n = 1 ∞ μ ( n ) n s <\displaystyle <\frac <1><\zeta (s)>>=\sum _
справедливо для любого s с действительной частью больше 1/2, с суммой в правой части сходящейся, эквивалентно гипотезе Римана. Из этого мы также можем сделать вывод, что если функция Мертенса определяется как
затем утверждение, что
M ( x ) = O ( x 1 2 + ε ) <\displaystyle M(x)=O\left(x^<<\frac <1><2>>+\varepsilon >\right)>
∑ i = 1 m | F n ( i ) − i m | = O ( n 1 2 + ϵ ) <\displaystyle \sum _
эквивалентно гипотезе Римана. Здесь
Гипотеза Линделёфа и рост дзета-функции [ править ]
Гипотеза Римана также подразумевает довольно точные ограничения на скорость роста дзета-функции в других областях критической полосы. Например, это означает, что
e γ ≤ lim sup t → + ∞ | ζ ( 1 + i t ) | log log t ≤ 2 e γ <\displaystyle e^<\gamma >\leq \limsup _6 π 2 e γ ≤ lim sup t → + ∞ 1 / | ζ ( 1 + i t ) | log log t ≤ 12 π 2 e γ <\displaystyle <\frac <6><\pi ^<2>>>e^<\gamma >\leq \limsup _
таким образом, скорость роста ζ (1+ it ) и обратная ей величина будут известны с точностью до 2 раз ( Titchmarsh 1986 ).
Гипотеза о большом промежутке между простыми числами [ править ]
Аналитические критерии, эквивалентные гипотезе Римана [ править ]
Было найдено множество утверждений, эквивалентных гипотезе Римана, хотя до сих пор ни одно из них не привело к значительному прогрессу в ее доказательстве (или опровержении). Вот некоторые типичные примеры. (В других используется функция делителей σ ( n ).)
выполняется для всех ε> 0 тогда и только тогда, когда выполняется гипотеза Римана.
Найман (1950) доказал, что гипотеза Римана верна тогда и только тогда, когда пространство функций вида
f ( x ) = ∑ ν = 1 n c ν ρ ( θ ν x ) <\displaystyle f(x)=\sum _<\nu =1>^
плотно в гильбертовом пространстве L 2 (0,1) квадратично интегрируемых функций на единичном интервале. Бёрлинг (1955) расширил это, показав, что дзета-функция не имеет нулей с вещественной частью больше 1 / p тогда и только тогда, когда это функциональное пространство плотно в L p (0,1).
Салем (1953) показал, что гипотеза Римана верна тогда и только тогда, когда интегральное уравнение
Последовательность Фарея обеспечивает две эквивалентности, благодаря Джерому Франелю и Эдмунду Ландау в 1924 году.
Φ ( u ) = ∑ n = 1 ∞ ( 2 π 2 n 4 e 9 u − 3 π n 2 e 5 u ) e − π n 2 e 4 u <\displaystyle \Phi (u)=\sum _.
Последствия обобщенной гипотезы Римана [ править ]
Исключенный средний [ править ]
Следует позаботиться о том, чтобы понять, что имеется в виду, когда говорят, что обобщенная гипотеза Римана ложна: следует точно указать, какой класс рядов Дирихле имеет контрпример.
Теорема Литтлвуда [ править ]
В 1914 году Литтлвуд доказал, что существуют сколь угодно большие значения x, для которых
и что существуют также сколь угодно большие значения x, для которых
Гипотеза числа классов Гаусса [ править ]
Теорема (Дойринг; 1933). Если RH ложно, то h ( D )> 1, если | D | достаточно большой
Теорема (Хайльбронн; 1934). Если обобщенная RH неверна для L- функции некоторого мнимого квадратичного характера Дирихле, то h ( D ) → ∞ при D → −∞.
В 1935 году Карл Сигель позже усилил результат, никоим образом не используя RH или GRH.
Рост тотента Эйлера [ править ]
Обобщения и аналоги [ править ]
Дирихле L-серия и другие числовые поля [ править ]
Функциональные поля и дзета-функции многообразий над конечными полями [ править ]
Арифметические дзета-функции арифметических схем и их L-факторы [ править ]
Дзета-функции Сельберга [ править ]
Сельберг (1956) ввел дзета-функцию Сельберга для римановой поверхности. Они похожи на дзета-функцию Римана: у них есть функциональное уравнение и бесконечное произведение, подобное произведению Эйлера, но взятое по замкнутым геодезическим, а не по простым числам. Формула следа Сельберга является аналогом для этих функций явных формул теории простых чисел. Сельберг доказал, что дзета-функции Сельберга удовлетворяют аналогу гипотезы Римана с мнимыми частями их нулей, связанными с собственными значениями лапласовского оператора римановой поверхности.
Дзета-функции Ихары [ править ]
Гипотеза парной корреляции Монтгомери [ править ]
Другие дзета-функции [ править ]
Попытки доказательства [ править ]
Теория операторов [ править ]
В 1999 году Майкл Берри и Джонатан Китинг предположили, что существует неизвестное квантование классического гамильтониана H = xp, так что H ^ <\displaystyle <\hat
N ( s ) = 1 π Arg ξ ( 1 / 2 + i s ) <\displaystyle N(s)=<\frac <1><\pi >>\operatorname >)>
то в подходе Берри – Конна
V − 1 ( x ) = 4 π d 1 / 2 N ( x ) d x 1 / 2 <\displaystyle V^<-1>(x)=<\sqrt <4\pi >><\frac
как было доказано Конном и другими, в этом подходе
Аналогия с гипотезой Римана над конечными полями предполагает, что гильбертово пространство, содержащее собственные векторы, соответствующие нулям, могло бы быть своего рода первой группой когомологий спектра Spec ( Z ) целых чисел. Денингер (1998) описал некоторые попытки найти такую теорию когомологий ( Leichtnam 2005 ).
Загир (1981) построил естественное пространство инвариантных функций на верхней полуплоскости, которое имеет собственные значения под оператором Лапласа, соответствующие нулям дзета-функции Римана, и заметил, что в маловероятном случае можно было бы показать существование подходящего положительного определенный внутренний продукт на этом пространстве, следовала бы гипотеза Римана. Картье (1982) рассмотрел связанный пример, где из-за причудливой ошибки компьютерная программа перечисляла нули дзета-функции Римана как собственные значения того же оператора Лапласа.
Schumayer & Hutchinson (2011) рассмотрели некоторые попытки построить подходящую физическую модель, связанную с дзета-функцией Римана.
Теорема Ли – Янга [ править ]
Результат Турана [ править ]
Пал Туран ( 1948 ) показал, что если функции
не иметь нулей, когда действительная часть s больше единицы, тогда
Некоммутативная геометрия [ править ]
Гильбертовы пространства целых функций [ править ]
Квазикристаллы [ править ]
Арифметические дзета-функции моделей эллиптических кривых над числовыми полями [ править ]
Когда человек переходит от геометрического измерения один, например, поля алгебраических чисел, к геометрическому измерению два, например, регулярной модели эллиптической кривой над числовым полем, двумерная часть обобщенной гипотезы Римана для арифметической дзета-функции модели имеет дело с полюсами дзета-функции. В измерении один изучение дзета-интеграла в тезисе Тейта не приводит к новой важной информации о гипотезе Римана. Напротив, во втором измерении работа Ивана Фесенкона двумерном обобщении тезиса Тейта включает интегральное представление дзета-интеграла, тесно связанного с дзета-функцией. В этой новой ситуации, невозможной в размерности один, полюса дзета-функции можно изучать с помощью дзета-интеграла и связанных групп аделей. Связанная с этим гипотеза Фесенко ( 2010 ) о положительности четвертой производной граничной функции, связанной с дзета-интегралом, по существу подразумевает полюсную часть обобщенной гипотезы Римана. Судзуки ( 2011 ) доказал, что последнее вместе с некоторыми техническими предположениями следует из гипотезы Фесенко.
Множественные дзета-функции [ править ]
Доказательство Делиня гипотезы Римана над конечными полями использовало дзета-функции многообразий произведений, чьи нули и полюсы соответствуют суммам нулей и полюсов исходной дзета-функции, чтобы ограничить действительные части нулей исходной дзета-функции. По аналогии Курокава (1992) ввел несколько дзета-функций, нули и полюсы которых соответствуют суммам нулей и полюсов дзета-функции Римана. Чтобы ряды сходились, он ограничился суммой нулей или полюсов с неотрицательной мнимой частью. Пока что известные оценки нулей и полюсов множественных дзета-функций недостаточно сильны, чтобы дать полезные оценки нулей дзета-функции Римана.
Расположение нулей [ править ]
Количество нулей [ править ]
Функциональное уравнение в сочетании с принципом аргумента подразумевает, что количество нулей дзета-функции с мнимой частью между 0 и T определяется выражением
N ( T ) = 1 π A r g ( ξ ( s ) ) = 1 π A r g ( Γ ( s 2 ) π − s 2 ζ ( s ) s ( s − 1 ) / 2 ) <\displaystyle N(T)=<\frac <1><\pi >>\mathop <\mathrm <2>>)\pi ^<-<\frac <2>>>\zeta (s)s(s-1)/2)>
1 π A r g ( Γ ( s 2 ) π − s / 2 s ( s − 1 ) / 2 ) = T 2 π log T 2 π − T 2 π + 7 / 8 + O ( 1 / T ) <\displaystyle <\frac <1><\pi >>\mathop <\mathrm <2>>)\pi ^<-s/2>s(s-1)/2)=<\frac
и небольшой, но довольно загадочный термин
H ( ln T ) 1 3 e − c ln ln T <\displaystyle H(\ln T)^<\frac <1><3>>e^<-c<\sqrt <\ln \ln T>>>>
точки, в которых функция S ( t ) меняет знак.
Сельберг (1946) показал, что средние моменты четных степеней S равны
Оценка Римана S ( T ) = O (log T ) подразумевает, что промежутки между нулями ограничены, и Литтлвуд немного улучшил это, показывая, что промежутки между их мнимыми частями стремятся к 0.
Теорема Адамара и де ла Валле-Пуссен [ править ]
| ζ ( σ ) 3 ζ ( σ + i t ) 4 ζ ( σ + 2 i t ) | ≥ 1 <\displaystyle |\zeta (\sigma )^<3>\zeta (\sigma +it)^<4>\zeta (\sigma +2it)|\geq 1>
для σ> 1, t вещественных, и глядя на предел при σ → 1. Это неравенство следует, взяв действительную часть журнала произведения Эйлера, чтобы увидеть, что
| ζ ( σ ) 3 ζ ( σ + i t ) 4 ζ ( σ + 2 i t ) | = exp ∑ p n p − n σ 3 + 4 cos ( t log p n ) + cos ( 2 t log p n ) n <\displaystyle |\zeta (\sigma )^<3>\zeta (\sigma +it)^<4>\zeta (\sigma +2it)|=\exp \sum _
что не меньше 1, потому что все слагаемые в сумме положительны из-за неравенства
3 + 4 cos ( θ ) + cos ( 2 θ ) = 2 ( 1 + cos ( θ ) ) 2 ≥ 0. <\displaystyle 3+4\cos(\theta )+\cos(2\theta )=2(1+\cos(\theta ))^<2>\geq 0.>
Нулевые регионы [ править ]
Нули на критической линии [ править ]
Харди (1914) и Харди и Литтлвуд (1921) показали, что на критической прямой бесконечно много нулей, рассматривая моменты некоторых функций, связанных с дзета-функцией. Сельберг (1942) доказал, что по крайней мере (малая) положительная доля нулей лежит на прямой. Левинсон (1974) улучшил это до одной трети нулей, связав нули дзета-функции с нулями ее производной, а Конри (1989) улучшил это еще до двух пятых.
Гипотезы Харди – Литтлвуда [ править ]
В 1914 году Годфри Гарольд Харди доказал, что у него бесконечно много действительных нулей. ζ ( 1 2 + i t ) <\displaystyle \zeta \left(<\tfrac <1><2>>+it\right)>
>
Гипотеза о дзета-функции Сельберга [ править ]
Численные расчеты [ править ]
π − s 2 Γ ( s 2 ) ζ ( s ) <\displaystyle \pi ^<-<\frac <2>>>\Gamma (<\tfrac <2>>)\zeta (s)>
имеет те же нули, что и дзета-функция в критической полосе, и действительна на критической прямой из-за функционального уравнения, поэтому можно доказать существование нулей точно на действительной прямой между двумя точками, проверяя численно, что функция имеет противоположные знаки в этих точках. Обычно пишут
ζ ( 1 2 + i t ) = Z ( t ) e − i θ ( t ) <\displaystyle \zeta (<\tfrac <1><2>>+it)=Z(t)e^<-i\theta (t)>>
где функция Харди Z и тета-функция Римана – Зигеля θ однозначно определяются этим и условием, что они являются гладкими действительными функциями с θ (0) = 0. Находя много интервалов, в которых функция Z меняет знак, можно показать, что на критической прямой много нулей. Чтобы проверить гипотезу Римана с точностью до данной мнимой части T нулей, необходимо также проверить, нет ли других нулей за пределами линии в этой области. Это можно сделать, вычислив общее количество нулей в области с помощью метода Тьюринга и проверив, что оно совпадает с количеством нулей, найденных в строке. Это позволяет проверить гипотезу Римана с помощью вычислений до любого желаемого значенияT (при условии, что все нули дзета-функции в этой области простые и находятся на критической прямой).
10 21 ) высоты
900 000 000 000 [7]
Они также подтвердили работу Гурдона (2004) и других.
Точки грамма [ править ]
| г −1 | γ 1 | г 0 | γ 2 | г 1 | γ 3 | г 2 | γ 4 | г 3 | γ 5 | г 4 | γ 6 | г 5 | ||
| 0,000 | 3,436 | 9,667 | 14,135 | 17,846 | 21,022 | 23,170 | 25,011 | 27,670 | 30,425 | 31,718 | 32,935 | 35,467 | 37 586 | 38,999 |
| г 124 | γ 126 | г 125 | г 126 | γ 127 | γ 128 | г 127 | γ 129 | г 128 |
|---|---|---|---|---|---|---|---|---|
| 279,148 | 279,229 | 280,802 | 282,455 | 282,465 | 283,211 | 284,104 | 284 836 | 285,752 |