Что такое ориентированный и неориентированный граф
Ориентированные и неориентированные графы



Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок) в графе не принимается во внимание.
 |
Ребро графа называется ориентированным, если этот порядок существенен. В этом случае говорят, что для ребра g = (xi, xj): xi – начальная, a xj – конечная вершины ребра.
Ориентированное ребро называют дугой графа (рис. 3.2).
Рис. 3.2. Дуга ориентированного графа
Граф называется неориентированным или неорграфом, если каждое ребро его не ориентированно, и ориентированным или орграфом, если каждое ребро его ориентированно. Если граф содержит ориентированные и неориентированные ребра, он называется смешанным.
Полным неориентированным графом называется граф U(X), ребрами которого являются всевозможные пары (xi, xj) для всех возможных вершин xi, xj Î X, i ¹ j.
В таком графе все вершины являются смежными (рис. 3.3).
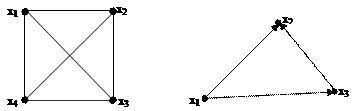 |
Рис. 3.3. Полные неориентированный и
Полным ориентированным графомU0(X) называется граф, у которого любые две вершины соединены хотя бы в одном направлении.

Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами или дугами (рис.3.5).
Рис. 3.5. Неориентированный и ориентированный мультиграфы
Дополнением графа G(X) является такой граф Gd(X), который совместно с графом G(X) образуют полный граф: U(X) = G(X) È Gd(X).
Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Вторым признаком является отсутствие или наличие кратных ребер.

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Понятие и представление графа: матрица смежности, список смежности
Определение графа
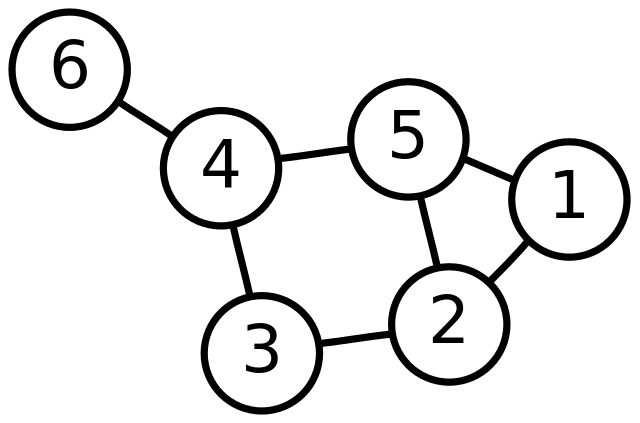
Этот граф состоит из 6 вершин, пронумерованных начиная с единицы, и 7 двухсторонних рёбер. Рёбра обычно записывают в виде пар вершин, которые они соединяют: \(1\)-\(2\), \(1\)-\(5\), \(2\)-\(3\), \(2\)-\(5\), \(3\)-\(4\), \(4\)-\(5\), \(4\)-\(6\).
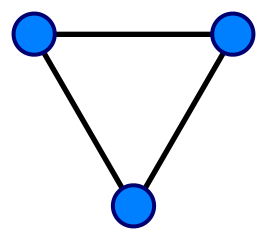
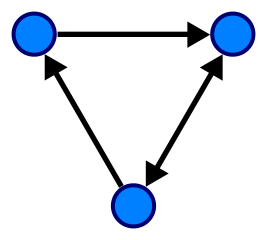
Ориентированные и неориентированные графы
Граф, в котором все рёбра неориентированные, также называют неориентированным, а граф с ориентированными рёбрами, соответственно, ориентированным.
 |  |
Пути и циклы
Путём в графе называется последовательность вершин, каждая из которых соединена со следующей ребром. Чаще всего под “путём” подразумевают простой путь, все вершины которого различны. Путь, который проходит через какую-либо вершину более одного раза называют сложным путём.
Если первая вершина пути совпадает с последней, то такой путь называют циклом.
Приведём примеры на этом графе:
Кратные рёбра и петли
Мультиграфы встречаются в задачах реже чем обычные графы (называемые простыми), но всё же встречаются, поэтому стоит иметь о них элементарное представление.
Связные графы
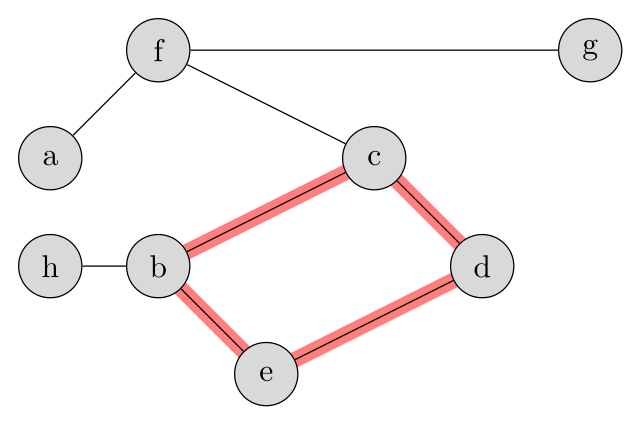
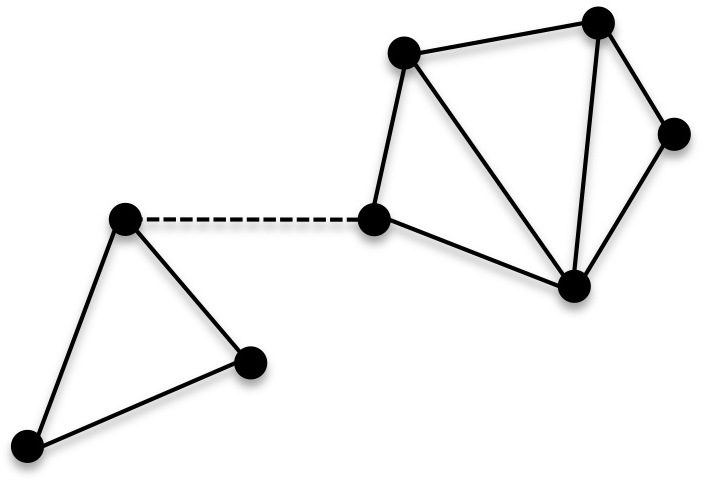
Граф называется связным если между любой парой вершин существует хотя бы один путь. Как пример рассмотрим следующий граф:
Одно из рёбер проведено штрихами. Если это ребро присутствует, то граф является связным. Если же его убрать, то связность теряется, граф разбивается на две части, друг с другом не связанные. Такие части называются компонентами связности.
Определение дерева
Все изображённые графы являются деревьями:
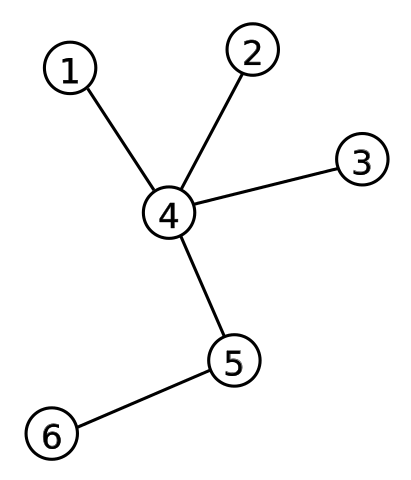
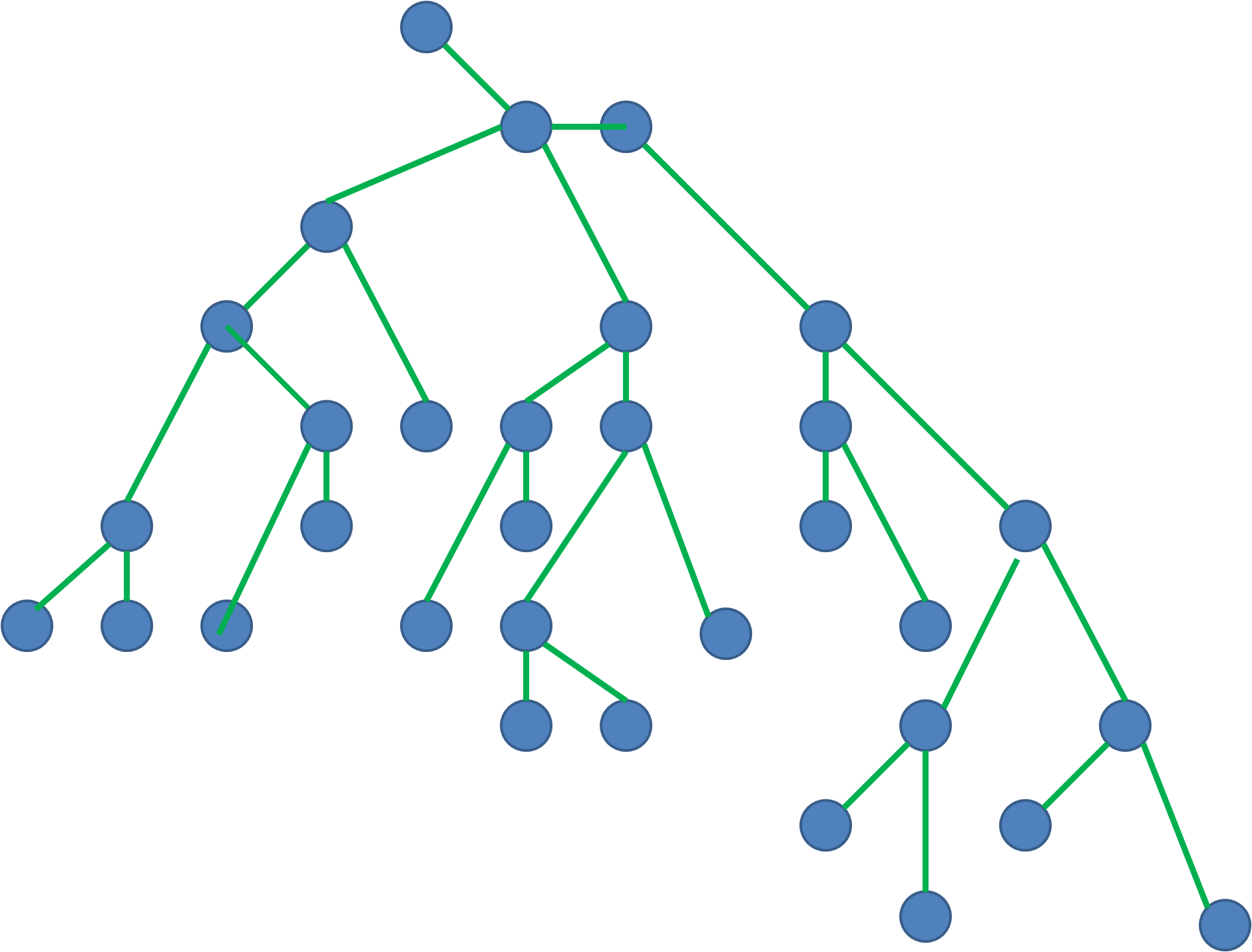
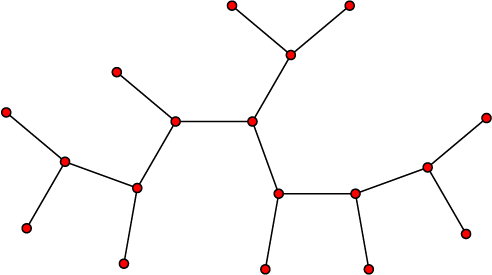
Среди множества свойств деревьев можно выделить два самых известных:
Матрица смежности
В качестве примера решим простую задачу: для каждой вершины графа выведем количество рёбер, смежных с ней.
Преимущества матрицы смежности:
Недостатки матрицы смежности:
Список смежности
Гораздо чаще для представления графов используется список смежности. Его идея заключается в хранении для каждой вершины расширяемого массива (вектора), содержащего всех её соседей.
Решим ту же задачу с использованием списка смежности (и С++11 для for-each):
Преимущества списка смежности:
Недостатки списка смежности:
brestprog
Олимпиадное программирование в Бресте и Беларуси
Что такое ориентированный и неориентированный граф
3.1 пТЙЕОФЙТПЧБООЩЕ Й ОЕПТЙЕОФЙТПЧБООЩЕ ЗТБЖЩ.
уРПУПВЩ ЪБДБОЙС ЗТБЖПЧ
V U E ПВТБЪХЕФ НОПЦЕУФЧП ЬМЕНЕОФПЧ ЗТБЖБ; РТЙ ЬФПН РТЕДРПМБЗБЕФУС, ЮФП е 
2. юБУФП ВЩЧБЕФ ЧБЦОП ПРТЕДЕМЙФШ, ЛБЛЙЕ ЗТБЖЩ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, Б ЛБЛЙЕ ОЕ ТБЪМЙЮБАФУС. пВЩЮОП ЬФП УЧСЪЩЧБАФ У РПОСФЙЕН ЙЪПНПТЖЙЪНБ ЗТБЖПЧ. дЧБ ЗТБЖБ G1= (V1, E1, з1) Й G2= (V2, е2, з2) ОБЪЩЧБАФУС ЙЪПНПТЖОЩНЙ, ЕУМЙ УХЭЕУФЧХАФ ЧЪБЙНОП ПДОПЪОБЮОЩЕ ПФПВТБЦЕОЙС f: V1 V2 Й g: е1 е2, УПИТБОСАЭЙЕ ЙОГЙДЕОФОПУФШ, Ф.Е. ФБЛЙЕ, ЮФП ДМС ЧУСЛПЗП Е ™ е, ТБЧЕОУФЧП з1(e) = (v1,v2) ЧМЕЮЕФ ЪБ УПВПК ТБЧЕОУФЧП з2 (gЕ) = (fv1, fv2).
чП НОПЗЙИ УМХЮБСИ НПЦОП ТБУУНБФТЙЧБФШ ЗТБЖЩ У ФПЮОПУФША ДП ЙЪПНПТЖЙЪНБ, Ф.Е. ОЕ ТБЪМЙЮБФШ ЙЪПНПТЖОЩЕ ЗТБЖЩ; ПДОБЛП, ЕУМЙ ЛБЛЙЕ-ФП ЧЕТЫЙОЩ ЙМЙ ТЕВТБ ЗТБЖПЧ ПВМБДБАФ ТБЪМЙЮОПК ЙОДЙЧЙДХБМШОПУФША, ОБРТЙНЕТ, ПОЙ ЪБОХНЕТПЧБОЩ ЙМЙ ЙН УПРПУФБЧМЕОЩ ЛБЛЙЕ-МЙВП ЮЙУМЕООЩЕ ИБТБЛФЕТЙУФЙЛЙ (ЧЕУ ТЕВТБ, ДМЙОБ ТЕВТБ Й ДТ.), ФП ЕУФЕУФЧЕООП РТЙ УТБЧОЕОЙЙ ДЧХИ ЗТБЖПЧ ЬФХ ЙОДЙЧЙДХБМШОПУФШ ХЮЙФЩЧБФШ.
3. уХЭЕУФЧХЕФ ОЕУЛПМШЛП УРПУПВПЧ ЪБДБОЙС ЗТБЖПЧ, УЧСЪБООЩИ У ТБЪМЙЮОПК ЖПТНПК ЪБДБОЙС ЖХОЛГЙЙ з. чПФ ОЕЛПФПТЩЕ ЙЪ ОЙИ ДМС ЛПОЕЮОЩИ
1) рЕТЕЮЙУМЕОЙЕ (УРЙУПЛ) ТЕВЕТ ЗТБЖБ У ХЛБЪБОЙЕН ЙИ ЛПОГПЧ Й ДПВБЧМЕОЙЕН УРЙУЛБ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО.
еУМЙ НБФТЙГБ ЙОГЙДЕОГЙК ЪБДБЕФ ЗТБЖ ПДОПЪОБЮОП, ФП НБФТЙГБ УПУЕДУФЧБ ЧЕТЫЙО ПРТЕДЕМСЕФ ЗТБЖ У ФПЮОПУФША ДП ЪБНЕОЩ МАВПЗП ОЕПТЙЕОФЙТПЧБООПЗП ТЕВТБ РБТПК РТПФЙЧПРПМПЦОП ОБРТБЧМЕООЩИ ДХЗ НЕЦДХ ФЕНЙ ЦЕ ЧЕТЫЙОБНЙ. пДОБЛП ДМС ЗТБЖПЧ ВЕЪ ЛТБФОЩИ ТЕВЕТ ЪБДБОЙЕ ЗТБЖБ Й ЬФПК НБФТЙГЕК ПДОПЪОБЮОП, ЬМЕНЕОФЩ НБФТЙГЩ УПУЕДУФЧБ ТБЧОЩ Ч ЬФПН УМХЮБЕ 0 ЙМЙ 1.
нПЦОП РПЛБЪБФШ, ЮФП ЧУСЛЙК ЗТБЖ У ЛПОЕЮОЩН (Й ДБЦЕ УЮЕФОЩН) ЮЙУМПН ЬМЕНЕОФПЧ НПЦЕФ ВЩФШ ТЕБМЙЪПЧБО Ч ФТЕИНЕТОПН РТПУФТБОУФЧЕ, РТЙЮЕН, ЕУМЙ ЗТБЖ ОЕ УПДЕТЦЙФ ЛТБФОЩИ ТЕВЕТ, ФП ТЕВТБ НПЦОП ТЕБМЙЪПЧБФШ РТСНПМЙОЕКОЩНЙ ПФТЕЪЛБНЙ. оБ РМПУЛПУФЙ ТЕБМЙЪХЕФУС ОЕ ЧУСЛЙК ЗТБЖ, ЮФП РПТПЦДБЕФ ТБЪДЕМЕОЙЕ ЗТБЖПЧ ОБ РМПУЛЙЕ Й ОЕРМПУЛЙЕ. фЕН ОЕ НЕОЕЕ ДБЦЕ ОЕРМПУЛЙК ЗТБЖ ВЩЧБЕФ ХДПВОП ЙЪПВТБЦБФШ ОБ РМПУЛПУФЙ, ОБДП ФПМШЛП ПФМЙЮБФШ ЧЕТЫЙОЩ ПФ РЕТЕУЕЮЕОЙК ТЕВЕТ ОБ ТЙУХОЛЕ (ОБРТЙНЕТ, ЙЪПВТБЦБФШ ЧЕТЫЙОЩ ЛТХЦЛБНЙ); ПТЙЕОФБГЙА ТЕВЕТ РПЛБЪЩЧБАФ УФТЕМЛБНЙ.
еУМЙ РТЕДУФБЧЙФШ ЗТБЖПН ХМЙЮОХА (ДПТПЦОХА) УЕФШ, ЗДЕ ТЕВТБ ЙЪПВТБЦБАФ ПФТЕЪЛЙ ДПТПЗ, УЧСЪЩЧБАЭЙЕ УПУЕДОЙЕ ЧЕТЫЙОЩ (РМПЭБДЙ Й РЕТЕЛТЕУФЛЙ), ФП ДМС ОЕВПМШЫПЗП ОБУЕМЕООПЗП РХОЛФБ ФБЛПК ЗТБЖ НПЦЕФ ВЩФШ РМПУЛЙН, ОП ДМС ЗПТПДБ У РХФЕРТПЧПДБНЙ, НПУФБНЙ Й ФТБОУРПТФОЩНЙ ТБЪЧСЪЛБНЙ Ч ТБЪОЩИ ХТПЧОСИ, ПО УЛПТЕЕ ЧУЕЗП ОЕРМПУЛЙК.
| A= |  | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  |
| -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
| B= |  | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 2 | 0 | 3 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4. тБУУНПФТЙН ОЕУЛПМШЛП РТЙНЕТПЧ ЗТБЖПЧ, ЙНЕАЭЙИ ЙОФЕТЕУОЩЕ РТЙНЕОЕОЙС.
оБ ТЙУХОЛЕ 2 Б, В, Ч ЙЪПВТБЦЕОЩ ЗТБЖЩ л3, л4, л5. оБ ТЙУХОЛЕ 2 З ЗТБЖ л5 РТЕДУФБЧМЕО У НЙОЙНБМШОЩН ЮЙУМПН РЕТЕУЕЮЕОЙК ЙЪПВТБЦЕОЙК ТЕВЕТ: ХУФТБОЙФШ ЙИ РПМОПУФША ОЕМШЪС.
 |  |  |  |
| a | В | Ч | З |
| тЙУХОПЛ 2 | |||
(3) n-НЕТОЩН ЕДЙОЙЮОЩН ЛХВПН ОБЪЩЧБЕФУС ЗТБЖ еn, ЧЕТЫЙОБНЙ ЛПФПТПЗП СЧМСАФУС ЧУЕ ОБВПТЩ ДМЙОЩ n ЙЪ ОХМЕК Й ЕДЙОЙГ, Б ТЕВТБ УПЕДЙОСАФ ЧЕТЫЙОЩ, ТБЪМЙЮБАЭЙЕУС ТПЧОП Ч ПДОПК ЛПНРПОЕОФЕ. уМХЮБЙ n = 3 Й n = 4 РТЕДУФБЧМЕОЩ ОБ ТЙУХОЛЕ 4 Б, В.
 |  |
| a | В |
| тЙУХОПЛ 4 | |
хРТБЦОЕОЙЕ. дПЛБЦЙФЕ, ЮФП ЗТБЖЩ еn СЧМСАФУС ДЧХДПМШОЩНЙ (ХЛБЪБОЙЕ: ТБУУНПФТЙФЕ ОБВПТЩ У ТБЪМЙЮОЩН ЮЙУМПН ЕДЙОЙГ).
5. зТБЖ о = (V’, е’) ОБЪЩЧБЕФУС РПДЗТБЖПН ЗТБЖБ G = (V, е), ПВПЪОБЮЕОЙЕ: о G, ЕУМЙ V’ V, е’ е Й ДМС НОПЦЕУФЧ V’ Й е’ УПИТБОСАФУС ЙОГЙДЕОГЙЙ ЗТБЖБ G. рТЙ ЬФПН, ПЮЕЧЙДОП, ЛБЦДПЕ ТЕВТП ЙЪ е’ ЧИПДЙФ Ч РПДЗТБЖ о ЧНЕУФЕ УП УЧПЙНЙ ЛПОГБНЙ.
йОПЗДБ ТБУУНБФТЙЧБАФУС ФПМШЛП РПДЗТБЖЩ ВЕЪ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО ЙМЙ ФПМШЛП РПДЗТБЖЩ, УПДЕТЦБЭЙЕ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ (Й ФПМШЛП ЮБУФШ ТЕВЕТ); ФБЛЙЕ РПДЗТБЖЩ РПМОПУФША ПРТЕДЕМСАФУС НОПЦЕУФЧПН УЧПЙИ ТЕВЕТ. ч ЬФЙИ УМХЮБСИ НПЦОП ЕУФЕУФЧЕООЩН ПВТБЪПН ПРТЕДЕМЙФШ ФЕПТЕФЙЛП-НОПЦЕУФЧЕООЩЕ ПРЕТБГЙЙ ОБД РПДЗТБЖБНЙ: РЕТЕУЕЮЕОЙЕ, ПВЯЕДЙОЕОЙЕ, УЙННЕФТЙЮЕУЛХА ТБЪОПУФШ (ОБЪЩЧБЕНХА ФБЛЦЕ УХННПК РП НПДХМА 2 ЙМЙ РТПУФП УХННПК), ДПРПМОЕОЙЕ ДП ЧУЕЗП ЗТБЖБ. рПДЗТБЖПН, ОБФСОХФЩН ОБ НОПЦЕУФЧП ЧЕТЫЙО V’ V ЗТБЖБ G, ОБЪЩЧБЕФУС РПДЗТБЖ, УПДЕТЦБЭЙК ЧЕТЫЙОЩ ЙЪ V Й ЧУЕ ТЕВТБ ЗТБЖБ G, УПЕДЙОСАЭЙЕ РБТЩ ЧЕТЫЙО ЙЪ V’.
рПДЗТБЖ Z 




дМС ЗТБЖБ, ЙЪПВТБЦЕООПЗП ОБ ТЙУХОЛЕ 1, s(v1) = 1, s(v2) = s(v3) = 3, s(v4)= 7,s(v6) = 0.
еУМЙ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ ЙНЕАФ ПДЙОБЛПЧХА УФЕРЕОШ s (ФБЛПК ЗТБЖ ОБЪЩЧБАФ ПДОПТПДОЩН), ФП УХННБ УФЕРЕОЕК ЕЗП ЧЕТЫЙО ТБЧОБ b • s, Б ЮЙУМП ТЕВЕТ ТБЧОП b • s / 2.
хРТБЦОЕОЙЕ. пРТЕДЕМЙФЕ ЮЙУМП ТЕВЕТ Ч ЗТБЖБИ е3, е4 (ТЙУХОПЛ 4Б, В).
ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ УХННБ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ТБЧОБ ХДЧПЕООПНХ ЮЙУМХ ТЕВЕТ m ЗТБЖБ, Ф.Е. ЮЕФОБ.
рЕФМС ДБЕФ ЧЛМБД 2 Ч УФЕРЕОШ ЧЕТЫЙОЩ.
пФУАДБ УМЕДХЕФ, ЮФП Ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ ЮЙУМП ЧЕТЫЙО ОЕЮЕФОПК УФЕРЕОЙ ЮЕФОП.
рЕФМС ДБЕФ ЧЛМБД 1 Ч ПВЕ ЬФЙ УФЕРЕОЙ.
ч ПТЗТБЖЕ УХННЩ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ρ1(ν) Й ρ2(ν) ТБЧОЩ ЛПМЙЮЕУФЧХ ТЕВЕТ m ЬФПЗП ЗТБЖБ, Б ЪОБЮЙФ, Й ТБЧОЩ НЕЦДХ УПВПК.
еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 0, Ф.Е. d(ν)=0, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЙЪПМЙТПЧБООПК. еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 1, d(ν)=1, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЛПОГЕЧПК ЙМЙ ЧЙУСЮЕК.
уХННБ УФЕРЕОЕК ЧЕТЫЙО ЗТБЖБ ТБЧОБ ХДЧПЕООПНХ ЛПМЙЮЕУФЧХ ТЕВЕТ.
нОПЦЕУФЧП ЧЕТЫЙО ЗТБЖБ ОБЪЩЧБЕФУС ОЕЪБЧЙУЙНЩН (ЧОХФТЕООЕ ХУФПКЮЙЧЩН), ЕУМЙ ОЙЛБЛЙЕ ДЧЕ ЧЕТЫЙОЩ ЙЪ ЬФПЗП НОПЦЕУФЧБ ОЕ УНЕЦОЩ. оЕЪБЧЙУЙНПЕ НОПЦЕУФЧП ЧЕТЫЙО ОБЪЩЧБЕФУС НБЛУЙНБМШОЩН, ЕУМЙ ПОП ОЕ СЧМСЕФУС УПВУФЧЕООЩН РПДНОПЦЕУФЧПН ОЕЛПФПТПЗП ДТХЗПЗП ОЕЪБЧЙУЙНПЗП НОПЦЕУФЧБ. оБЙВПМШЫЕЕ РП НПЭОПУФЙ ЙЪ НБЛУЙНБМШОЩИ ОЕЪБЧЙУЙНЩИ НОПЦЕУФЧ ОБЪЩЧБЕФУС ОБЙВПМШЫЙН. юЙУМП ЧЕТЫЙО Ч ОБЙВПМШЫЕН ОЕЪБЧЙУЙНПН НОПЦЕУФЧЕ ЗТБЖБ G ОБЪЩЧБЕФУС ЮЙУМПН ОЕЪБЧЙУЙНПУФЙ (ЮЙУМПН ЧОХФТЕООЕК ХУФПКЮЙЧПУФЙ, ОЕРМПФОПУФША) Й ПВПЪОБЮБЕФУС ЮЕТЕЪ α0(G).
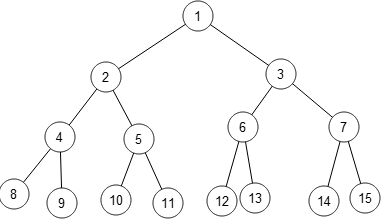
оБ ТЙУХОЛЕ 5 РПЛБЪБО ЗТБЖ G, Х ЛПФПТПЗП ЮЙУМП ОЕЪБЧЙУЙНПУФЙ α0(G)=4. нОПЦЕУФЧП ЧЕТЫЙО <ν1,ν2,ν3,ν7>; <ν1,ν2,ν3,ν8>; <ν2,ν3,ν5,ν7>; <ν2,ν3,ν5,ν8> СЧМСАФУС ОБЙВПМШЫЙНЙ ОЕЪБЧЙУЙНЩНЙ НОПЦЕУФЧБНЙ. нОПЦЕУФЧП ЧЕТЫЙО <ν4,ν7> СЧМСЕФУС НБЛУЙНБМШОЩН ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН, ОП ОЕ ОБЙВПМШЫЙН.
оЕЪБЧЙУЙНЩЕ НОПЦЕУФЧБ ТЕВЕТ ЗТБЖБ G ОБИПДСФУС ЧП ЧЪБЙНОП ПДОПЪОБЮОПН УППФЧЕФУФЧЙЙ У ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН ЧЕТЫЙО ТЕВЕТОПЗП ЗТБЖБ L(G), Ф.Е. α1(G)=α0((L)G)).
Основные определения теории графов
Содержание
Ориентированные графы [ править ]
| Определение: |
| Конечным графом (англ. finite graph) [math]G[/math] называется граф, в котором множества [math]V[/math] и [math]E[/math] — конечны. Следует заметить, что большинство рассматриваевых нами графов — конечны. |
| Определение: |
| Изоморфные графы (англ. isomorphic graphs) — два графа [math]A[/math] и [math]B[/math] называются изоморфными, если можно установить биекцию между их вершинами и соответствующими им рёбрами. |
Инцидентность (англ. incidence) — понятие, используемое только в отношении ребра и вершины. Две вершины или два ребра не могут быть инцидентны.
Заметим, что по определению ориентированного графа, данному выше, любые две вершины [math]u,
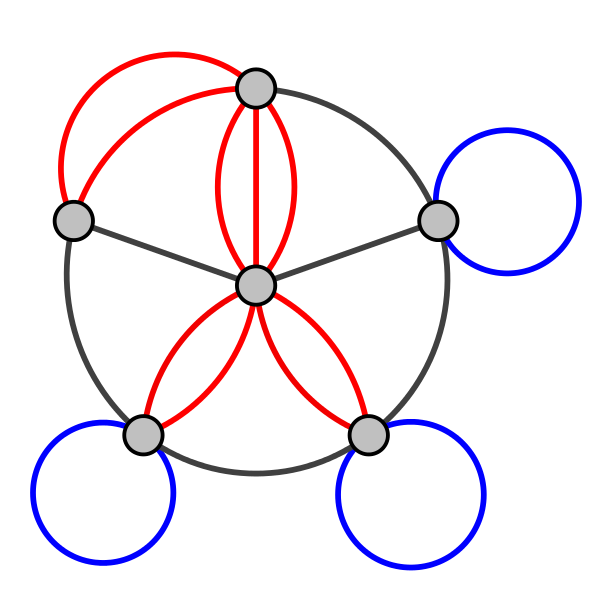
Данное определение разрешает соединять вершины более чем одним ребром. Такие рёбра называются кратными (иначе — параллельные, англ. multi-edge, parallel edge). Граф с кратными рёбрами принято называть мультиграфом (англ. multigraph). Если в мультиграфе присутствуют петли, то такой граф называют псевдографом (англ. pseudograph).