Что такое орта геометрия

Прямоугольная система координат

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.

Содержание

Прямоугольная система координат на плоскости

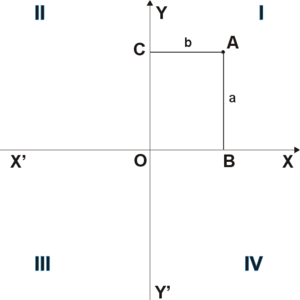
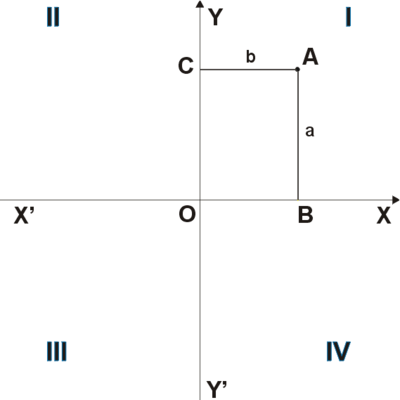
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат и . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление.

Положение точки на плоскости определяется двумя координатами и . Координата равна длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки и определяются линиями, проведёнными из точки параллельно осям и соответственно.

При этом координате приписывается знак минус, если точка лежит на луче (а не на луче , как на рисунке). Координате приписывается знак минус, если точка лежит на луче . Таким образом, и являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Координата называется абсциссой точки , координата — ординатой точки .

Символически это записывают так:

или указывают принадлежность координат конкретной точке с помощью индекса:

Прямоугольная система координат в пространстве

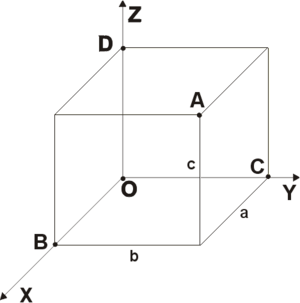
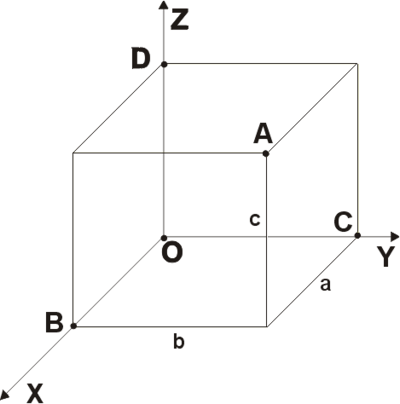
Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трехмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат , и . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно [2] ) одинаковы для всех осей. — ось абсцисс, — ось ординат, — ось аппликат.

Положение точки в пространстве определяется тремя координатами , и . Координата равна длине отрезка , координата — длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки , и определяются плоскостями, проведёнными из точки параллельно плоскостям , и соответственно.

Координата называется абсциссой точки , координата — ординатой точки , координата — аппликатой точки .

Символически это записывают так:

или привязывают запись координат к конкретной точке с помощью индекса:

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка лежала не как на рисунке — на луче , а на его продолжении в обратную сторону от точки (на отрицательной части оси ), то абсцисса точки была бы отрицательной (минус расстоянию ). Аналогично и для двух других осей.

Прямоугольные все системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами [3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта итп (положительное направление осей выбирают так, чтобы при повороте оси против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси , если этот поворот наблюдать со стороны положительного направления оси ).

Прямоугольная система координат в многомерном пространстве

Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать ее n).

Для обозначения координат обычно [4] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:

Для обозначения произвольной i-ой координаты из этого набора используют буквенный индекс:

а нередко обозначение используют и для обозначения всего набора, подразумевая, что индекс пробегает весь набор значений: .

Прямоугольные координаты вектора

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

2. Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

В прямоугольных координатах очень просто записываются все операции над векторами:

а отсюда и вычитание и деление:

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

(Только в прямоугольных координатах с единичным масштабом по всем осям).

для любой размерности пространства,

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

В трёхмерном случае такие орты обычно обозначаются

, и

, и .

Могут также применяться обозначения со стрелками (, и или , и ) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

Для более высоких, чем 3, размерностей (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто [10] это

Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):

а для ортонормированного базиса координаты еще и очень легко найти через скалярные произведения с ортами:

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

Использование ортов восходит, по-видимому, к Гамильтону и Максвеллу.

Источник

Что такое орта геометрия

Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.

Векторная алгебра с нуля!

Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.

Книги по изучению физики и для подготовки к ЕГЭ

Единичные векторы. Орты. Декартова система координат

Очевидно, а = а·а_е (а — модуль вектора а). Это следует из правила, по которому выполняется операция умножения скаляра на вектор.

Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i, j, k.

Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i, а τ. Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности – к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль – это одно и то же). Орт этой оси обозначают уже не j, а n. Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это – бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.

Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

Источник

Декартова система координат

Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.

Содержание

Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

См. также

Ссылки

Полезное

Смотреть что такое «Декартова система координат» в других словарях:

ДЕКАРТОВА СИСТЕМА КООРДИНАТ — ДЕКАРТОВА СИСТЕМА КООРДИНАТ, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене). Декарт впервые ввел… … Энциклопедический словарь

ДЕКАРТОВА СИСТЕМА КООРДИНАТ — прямоугольная система координат на плоскости или в пространстве, в которой масштабы по осям одинаковы и оси координат взаимно перпендикулярны. Д. с. к. обозначается буквами x:, у для точки на плоскости или x, у, z для точки в пространстве. (См.… … Большая политехническая энциклопедия

ДЕКАРТОВА СИСТЕМА КООРДИНАТ — ДЕКАРТОВА СИСТЕМА КООРДИНАТ, система, введенная Рене ДЕКАРТОМ, в которой положение точки определяется расстоянием от нее до взаимно пересекающихся линий (осей). В простейшем варианте системы оси (которые обозначаются как х и у) перпендикулярны.… … Научно-технический энциклопедический словарь

декартова система координат — Dekarto koordinačių sistema statusas T sritis fizika atitikmenys: angl. Cartesian system; Cartesian system of co ordinates vok. cartesisches Koordinatensystem, n; kartesisches Koordinatensystem, n rus. декартова система, f; декартова система… … Fizikos terminų žodynas

Декартова система координат — прямолинейная система координат (См. Координаты) на плоскости или в пространстве (обычно с одинаковыми масштабами по осям). Сам Р. Декарт в «Геометрии» (1637) употреблял только систему координат на плоскости (вообще, косоугольную). Часто… … Большая советская энциклопедия

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В… … Википедия

декартова система — Dekarto koordinačių sistema statusas T sritis fizika atitikmenys: angl. Cartesian system; Cartesian system of co ordinates vok. cartesisches Koordinatensystem, n; kartesisches Koordinatensystem, n rus. декартова система, f; декартова система… … Fizikos terminų žodynas

СИСТЕМА КООРДИНАТ — совокупность условий, определяющих положение точки на прямой, на плоскости, в пространстве. Существуют различные С. к.: декартова, косоугольная, цилиндрическая, сферическая, криволинейная и др. Линейные и угловые величины, определяющие положение… … Большая политехническая энциклопедия

ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ — ортонормированная прямолинейная система координат в евклидовом пространстве. Д. п. с. к. на плоскости задается двумя взаимно перпендикулярными прямыми осями координат, на каждой из к рых выбрано положительное направление и задан отрезок единичной … Математическая энциклопедия

Прямоугольная система координат — Прямоугольная система координат прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… … Википедия

Источник