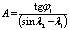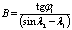Что такое ортодромическое расстояние
Ортодромия
Ортодромия, ортодрома (из др.-греч. ὀρθός «прямой» + δρόμος «бег, путь») — кратчайшая линия между двумя точками на поверхности вращения. В картографии и навигации — название геодезической линии кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящей через эти точки. В отличие от локсодромии ортодромия пересекает меридианы под разными углами. В судо- и самолётовождении, где Земля принимается за шар, ортодромия представляет собой дугу большого круга.
Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.
В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.
Параллели (за исключением экватора) не являются ортодромиями.
Содержание
Расчёт ортодромии
Обозначения: D — длина ортодромии, φ1 — широта точки отбытия, λ1 — долгота точки отбытия, φ2 — широта точки прибытия, λ2 — долгота точки прибытия, φ — широта промежуточной точки, λ — долгота произвольно взятой промежуточной точки ортодромии, 111,12 — длина дуги 1° меридиана (может быть выбрана иная величина).
Для примера возьмём перелёт из Внукова (координаты: 55°35′46″ с. ш., 37°16′03″в. д.) в Пулково (координаты: 59°48′01″ с. ш., 30°15′45″в. д.).
В десятичном выражении координаты точек отбытия и прибытия выглядят так: 55,596111, 37,2675 и 59,8002778, 30,2625. Длина дуги 1° меридиана — 111,3 км.
Находим длину ортодромии: sin55,596111 * sin59,8002778 + cos55,596111 * cos59,8002778 * cos(30,2625 — 37,2675) = 0,825075 * 0,864277 + 0,565023 * 0,5030158 * 0,9925355 = 0,71309335 + 0,282094 = 0,99518735. acos0,99518735 = 5,62346633. 5,62346633 * 111,3 = 625,892 км.
Находим начальный азимут: cos55,596111 tg59,8002778 / sin(30,2625 — 37,2675) — sin55,596111 / tg(30,2625 — 37,2675) = 0,565023 * 1,7181812 / (-0,121956)- 0,825075 / (-0,122873) = −7,9603455 + 6,71486 = −1,2454855. −1,2454855 −1 = −0,80289975. tg(-0,80289975) = −38,761° = 321,239°.
Находим конечный азимут: sin59,8002778 / tg(30,2625 — 37,2675) — cos59,8002778 * tg55,596111 / sin(30,2625 — 37,2675) = 0,864277 / (-0,122873) — 0,5030158 * 1,4602505 / (-0,121956) = −7,033905 — (-6,024605) = −1,0093. −1,0093 −1 = −0,990786. atg(-0,990786) = −44,73481 = 315,2652° или 315°15′55″.
В геометрии
См. также
Примечания
Ссылки
Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)
Полезное
Смотреть что такое «Ортодромия» в других словарях:
ортодромия — ортодрома, дуга, линия Словарь русских синонимов. ортодромия сущ., кол во синонимов: 3 • дуга (19) • линия … Словарь синонимов
Ортодромия — линия кратчайшего расстояния между двумя точками на поверхности земного шара или земного эллипсоида. Название «Ортодромия» принято в навигации и картографии. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
ОРТОДРОМИЯ — (ортодрома) (от греч. orthos прямой и dromos бег путь), кратчайшая линия между двумя точками сферы (или какой либо другой поверхности вращения) … Большой Энциклопедический словарь
ортодромия — и, ж. orthodromie <гр. orthos прямой + dromos путь. 1. геом. Кратчайшая линия межу двумя точками сферы (или какой н. другой поверхности вращения). 2. авиа., мор. Линия движения корабля или самолета, представляющая собой отрезок дуги большой… … Исторический словарь галлицизмов русского языка
ортодромия — Линия кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящий через эти точки. → Рис. 205, с. 450 … Словарь по географии
ортодромия — ортодрома (от греч. orthós прямой и drómos бег, путь), кратчайшая линия между двумя точками сферы (или какой либо другой поверхности вращения). * * * ОРТОДРОМИЯ ОРТОДРОМИЯ (ортодрома) (от греч. orthos прямой и dromos бег, путь), кратчайшая… … Энциклопедический словарь
Ортодромия — 6. Ортодромия Линия на земном шаре, соединяющая две точки по кратчайшему расстоянию Источник: ГОСТ 23634 83: Морская навигация и морская гидрография. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
ОРТОДРОМИЯ — Происхождение: ортодрома, от греч. orthos прямой и dromos бег, путь дуга большого круга, проходящая через 2 точки на поверхности шара и являющаяся кратчайшим расстоянием между ними. Ортодромия на мор. картах в меркаторской проекции изображается… … Морской энциклопедический справочник
Ортодромия — (от греч. orthós прямой и drómos бег, путь) кратчайшая линия между двумя точками на поверхности вращения. В кораблевождении и самолётовождении, где Земля принимается за шар, О. представляет собой дугу большого круга. В противоположность… … Большая советская энциклопедия
Что такое ортодромическое расстояние
Значения ортодромических расстояний от международных аэропортов Российской Федерации до зарубежных аэропортов
В целях сокращения переписки с органами исполнительной власти с июня 2008г. на Интернет — сайте ГЦ ЕС ОрВД размещены «Значения ортодромических расстояний от международных аэропортов Российской Федерации до зарубежных аэропортов».
В состав информации включены следующие данные:
— колонка № 1- наименование аэропорта вылета из Российской Федерации (А/п вылета);
— колонка № 2- наименование аэропорта первой посадки вне Российской Федерации (А/п назначения (первая посадка);
— колонка №3- наименование государства, которому принадлежит аэродром первой посадки вне Российской Федерации (Государство);
— колонка № 4- общая ортодромия между аэропортом вылета из Российской Федерации и аэропортом первой посадки вне Российской Федерации (в километрах) (Общая ортодромия, км);
— колонка № 5- ортодромия между аэропортом вылета из Российской Федерации и точкой выхода из воздушного пространства Российской Федерации (в километрах) ( Ортодромия по РФ, км);
— колонка № 6- отношение ортодромии между аэропортом вылета из Российской Федерации и точкой выхода из воздушного пространства Российской Федерации к ортодромии между аэропортом вылета из Российской Федерации и аэропортом первой посадки вне Российской Федерации (в процентах) (Отношение ортодромии по РФ к общей ортодромии, %)
Поиск нужной информации необходимо выполнять по наименованию аэропортов назначения (первой посадки), размещенных в таблице (колонка № 2) в алфавитном порядке.
Примечание. В некоторых случаях указанные в различных документах наименования городов и соответствующие им названия аэропортов не совпадают.
Например: в авиабилетах применяются записи:
— Балатон — соответствует аэропорту Шармеллек (Балатон) (ВЕНГРИЯ);
— Байконур — соответствует аэропорту Крайний (КАЗАХСТАН);
— Бейинг — соответствует аэропорту Пекин (Столичный) (КИТАЙ);
— Бодрум Милас — соотв. аэропорту Мугла (Милас — Бодрум) (ТУРЦИЯ);
— Даламан — соответствует аэропорту Мугла (Даламан) (ТУРЦИЯ);
— Даболим — соответствует аэропорту Гоа (Даболим) (ИНДИЯ);
— Денпасар — соответствует аэропорту Бали (ИНДОНЕЗИЯ);
— Ибица — соответствует аэропорту Ивиса (ИСПАНИЯ);
— Корфу — соотв. аэропорту Керкира (Иоанис Каподистриас), ГРЕЦИЯ;
— Лас-Пальмас — соответствует аэропорту Ла Пальма (ИСПАНИЯ);
— Марко Поло — соответствует аэропорту Венеция (Тессера) (ИТАЛИЯ);
— Маэ — соотв. аэропорту Сейшелы (СЕЙШЕЛЬСКИЕ ОСТРОВА);
— Нижнекамск — соответствует аэропорту Бегишево (РОССИЯ);
— Нхатранг — соответствует аэропорту Камрань (ВЬЕТНАМ);
— Патрас — соответствует аэропорту Араксос (ГРЕЦИЯ);
— Самуй — соответствует аэропорту Сурат Тахни (Самуй) (ТАИЛАНД);
— Семипалатинск — соответствует аэропорту Семей (КАЗАХСТАН);
— Таллинн — соответствует аэропорту Леннарт Мери Таллинн (Эстония);
— Теркира Исланд — соотв. аэропорту Ладжес (ПОРТУГАЛИЯ);
— Утапау (Паттая) — соответствует аэропорту Районг (Утапау Паттая) (ТАИЛАНД);
— Фуншал — соответствует аэропорту Мадейра (ПОРТУГАЛИЯ);
— Хайлар — соответствует аэропорту Хулунбуир (Хайлар) (КИТАЙ);
— Хайнань — соответствует аэропорту Санья (Феникс) (КИТАЙ);
— Чимкент — соответствует аэропорту Шымкент (КАЗАХСТАН).
Опубликованная информация обновляется по мере появления новых (дополнительных) данных и в случаях их изменения.
В случаях отсутствия в таблице информации по необходимым ортодромическим расстояниям можно направить официальный запрос органа исполнительной власти (почтовой связью) по предлагаемой форме:
ОБРАЗЕЦ:
Генеральному директору
ФГУП «Госкорпорация по ОрВД»
В. М. Горбенко
125993, г. Москва, А-167, ГСП-3,
Ленинградский проспект, 37
Прошу предоставить информацию об ортодромии по Российской Федерации, общей ортодромии и процентном отношении ортодромии по Российской Федерации к общей ортодромии по маршруту Москва (Внуково) — Неаполь (ИТАЛИЯ) — Москва (Внуково).
Приложение: копия авиабилетов (посадочных талонов) — на 1 листе.
Подпись руководителя учреждения.
Ф.И.О. и контактные телефоны исполнителя документа
В качестве приложения к запросу требуется представление ксерокопии авиабилета (посадочных талонов) с разборчивыми читаемыми полями.
Контактные телефоны должностных лиц ФГУП «Госкорпорация по ОрВД» по вопросам предоставления информации по ортодромиям: тел.: (495) 601-07-19; 601-07-06; факс: (495) 601-07-01.
Значения ортодромических расстояний
от международных аэропортов Российской Федерации
до зарубежных аэропортов
(СЕНТЯБРЬ 2012г.)
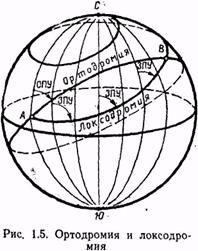
Локсодромия и Ортодромия.
Локсодромией, или кривой равных путевых углов, называется линия, пересекающая меридианы под одинаковыми углами.
На поверхности земного шара локсодромия имеет вид пространственной спирали, с каждым оборотом вокруг земного шара асимптотически приближающейся к полюсу.
Кроме частных случаев, когда локсодромия и ортодромия совпадают (полет по меридиану или экватору), локсодромия длиннее ортодромии и обращена выпуклостью всегда к экватору.
Максимальное увеличение пути при полете по локсодромии, в сравнении с полетом по ортодромии, в зависимости от разности долгот ИПМ п КПМ (Х2—Я^), и значение широты, при которой увеличение пути максимально.
Полеты по локсодромии в настоящее время, особенно на самолетах с ГТД, практического применения не имеют, а поэтому прокладка локсодромии на полетной карте здесь не разбирается. Следует лишь отметить, что локсодромию большой протяженности следует прокладывать по точкам. Для этого необходимо предварительно рассчитать путевой угол и координаты ее промежуточных точек. Элементы локсодромии можно рассчитать по формулам или определить графически при помощи картографической сетки в меркаторской проекции.
Задаваясь долготой промежуточной точки, находят величину D, являющуюся функцией широты. Широту ф промежуточной точки находят по D при помощи специальных таблиц, прилагаемых к учебникам авиационной картографии.
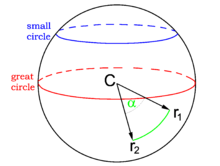
Ортодромией называется линия кратчайшего расстояния между двумя точками на земной поверхности. Ортодромия является дугой большого круга, плоскость которого проходит через центр земного шара и две заданные точки на поверхности земного шара. Меридианы являются ортодромиями, соединяющими северный и южный географические полюса, — это частные случаи ортодромии. В общем случае ортодромия пересекает меридианы под различными, неравными между собой углами.
Опорный меридиан (ОМ) — меридиан, проходящий через начальную точку ортодромии участка. Расчеты или измерения ортодромического направления полета самолета выполняют от опорного меридиана.
Уравнение локсодромии на поверхности земного шара
Кроме частных случаев, когда локсодромия и ортодромия совпадают (полет по меридиану или экватору), локсодромия длиннее ортодромии и обращена выпуклостью всегда к экватору.
Максимальное увеличение пути при полете по локсодромии, в сравнении с полетом по ортодромии, в зависимости от разности долгот ИПМ п КПМ (Х2—Я^), и значение широты, при которой увеличение пути максимально.
Полеты по локсодромии в настоящее время, особенно на самолетах с ГТД, практического применения не имеют, а поэтому прокладка локсодромии на полетной карте здесь не разбирается. Следует лишь отметить, что локсодромию большой протяженности следует прокладывать по точкам. Для этого необходимо предварительно рассчитать путевой угол и координаты ее промежуточных точек. Элементы локсодромии можно рассчитать по формулам или определить графически при помощи картографической сетки в меркаторской проекции.
Задаваясь долготой промежуточной точки, находят величину D, являющуюся функцией широты. Широту ф промежуточной точки находят по D при помощи специальных таблиц, прилагаемых к учебникам авиационной картографии.
Ортодромией называется линия кратчайшего расстояния между двумя точками на земной поверхности. Ортодромия является дугой большого круга, плоскость которого проходит через центр земного шара и две заданные точки на поверхности земного шара. Меридианы являются ортодромиями, соединяющими северный и южный географические полюса, — это частные случаи ортодромии. В общем случае ортодромия пересекает меридианы под различными, неравными между собой углами.
Опорный меридиан (ОМ) — меридиан, проходящий через начальную точку ортодромии участка. Расчеты или измерения ортодромического направления полета самолета выполняют от опорного меридиана.
Начальный азимут ортодромии (А) — угол, образованный северным направлением меридиана, проходящего через начальную точку ортодромии, и ортодромией.
При полете по ортодромии следует помнить, что ИПУ ортодромии изменяется на угол б — угол схождения меридианов, который можно вычислить по приближенной формуле
Элементы ортодромии (длина, координаты промежуточных точек и ортодромическнй путевой угол) могут быть вычислены по формулам сферической тригонометрии или графически.
3-й способ. ОПУ может быть измерен непосредственно на карте от любого меридиана с последующим внесением поправки на угол сближения опорного меридиана и меридиана места измерения углов.
Для выполнения полета по ЛЗП в обратном направлении замер ортодромических путевых углов происходит от меридианов, бывших конечными при полете в первоначальном направлении. Следовательно, путевые углы при полете туда и обратно будут отличны друг от друга не только на 180°, но и на величину поправки на сближение меридианов.
Если весь маршрут полета проходит по ортодромии и не имеет ПГ1М, то расчет путевых углов значительно упрощается:
1) маршрут разбивают на участки по 1 000—1200 км.
2) меридианы начальных точек участков считают опорными для обоих направлений и от них измеряют ортодромические путевые углы.
Изображение ортодромии на картах в различных проекциях. На картах, составленных в равноугольной цилиндрической проекции (проекции Меркатора), ортодромия изображается в виде сложной кривой, всегда обращенной выпуклостью к географическим полюсам.
На картах центральной проекции все ортодромии изображаются прямой линией.
На картах в полярной стереографической проекции ортодромия в общем случае изображается дугой окружности. Кривизна ортодромии тем меньше, чем ближе она расположена к географическому полюсу. Меридианы, являющиеся частным случаем ортодромии, на картах полярной стереографической проекции изображаются прямыми линиями.
На бортовой аэронавигационной карте масштаба 1 : 2 000 000, составленной в видоизмененной поликонической проекции, ортодромия в пределах одного листа практически представляет собой прямую линию.
Линией равных азимутов (ЛРА), или равных радиопеленгов, называется линия, в каждой точке которой наземная радиостанция пеленгуется под одним и тем же углом (ЙПР). При помощи линии равных азимутов как линии положения определяют место самолета по наземным импульсным маякам при помощи бортового радиолокатора Линия равных азимутов — сложная кривая. На земном шаре она пересекает меридианы под различными углами и лишь с меридианом, проходящим через точку установки радиостанции, она составляет угол, равный истинному пеленгу радиостанции (ИПР).
(ЛРР) называется линия на земной поверхности, все точки которой находятся от некоторой определенной точки на одинаковом удалении — на окружности малого круга земного шара. Как линия положения, линия равных расстояний в самолетовождении применяется при астрономических измерениях высоты светила с помощью секстанта. В авиационной астрономии ЛРА носит название круга равных высот, на карте она заменяется касательной — прямой равных высот. Элементы этой линии рассчитывают при помощи специальных таблиц высот и азимутов светил — ТВА.
ЛРР используют при применении угломерно-дальномерных и двухполюсных дальномерных радиотехнических систем.
На картах разных проекций ЛРР имеют различный вид. На картах стереографической проекции ЛРР — окружности.
ЛРР наносят на карты с большой степенью точности по промежуточным точкам ЛРР, вычисленным по формулам прямой и обратной геодезических задач (расчеты производятся на поверхности эллипсоида Красовского).
Гиперболой (сферической), или линией равных разностей расстояний, является кривая, в каждой точке которой разность расстояний до двух фиксированных точек (радиостанций) есть величина постоянная. Для целей самолетовождения с использованием линий равных разностей расстояний существуют гиперболические системы навигации. Такие системы включают в себя две пары (или цепочку) наземных станций и бортовое оборудование (приемо-индикаторы), позволяющие с достаточной точностью измерить разность расстояний от самолета до радиостанций.
Место самолета по гиперболической системе определяют пересечением двух гипербол.
Карта — условное уменьшенное обобщенное, построенное по определенным математическим правилам изображение земной поверхности на плоскости.
План — изображение на плоскости в крупном масштабе небольших участков земной поверхности, принимаемых за плоскость.
Картографическая проекция — способ изображения поверхности земного шара или земного эллипсоида на плоскости.
Масштаб — отношение длины линии на карте к длине соответствующей линии на поверхности Земли.
Главный масштаб (М) показывает, во сколько раз уменьшен земной шар (или эллипсоид) при проектировании его на плоскость. Главный масштаб всегда указывается на карте.
Частный масштаб (ц) определяется как отношение бесконечно малого отрезка на карте в данной точке и по данному направлению к соответствующему бесконечно малому отрезку на поверхности земного шара (или эллипсоида).
Частный масштаб в направлении меридиана обозначается буквой т, а в направлении параллели — буквой п.
Главными направлениями называются направления, по которым частные масштабы или минимальны, пли максимальны. Максимальный и минимальный масштабы в данной точке обозначаются а и б. Почти во всех проекциях карт, применяемых в самолетовождении, главные направления совпадают с меридианами и параллелями.
Увеличение масштаба с определяется отношением частного масштаба к главному
Искажение длин У определяется разностью между увеличением масштаба и единицей.
Искажение направлений со определяется разностью между направлением на земном шаре и тем же направлением на карте. Максимальное искажение направлений в данной точке вычисляют по формуле
Масштабом площади р называется отношение площади бесконечно малого участка на карте к соответствующей площади на поверхности глобуса, до размера которого уменьшен земной шар перед проектированием его на плоскость. Искажение площадей характеризуется величиной масштаба площади.
По характеру искажения катографические проекции подразделяются на равноугольные, равнопромежуточные, равновеликие и произвольные.
Равноугольные проекции характеризуются тем, что углы и направления на картах, составленных в этих проекциях, изображены без искажений; частные масштабы по главным направлениям равны между собой; бесконечно малые фигуры на карте сохраняют подобие соответствующим фигурам на земном шаре. Эти данные выражаются следующим образом: a — b; ы = 0; р = ab.
Равноугольные проекции позволяют наиболее просто определять направления и поэтому нашли широкое применение при создании авиационных карт, так как для самолетовождения важно точное измерение направления.
Равнопромежуточными называются проекции, в которых частные масштабы во всех точках по одному из главных направлений равны главному масштабу.
Равновеликими называются проекции, в которых площадь изображаемой фигуры равна площади той же фигуры на карте.
Произвольными называются проекции, которые не равноугольны, не равно-промежуточны и не равновелики.
Произвольные проекции имеют практически очень небольшие искажения в направлениях, длинах и площадях и поэтому нашли широкое применение в самолетовождении. Аэронавигационная карта масштаба 1 : 2 000 000 составлена в видоизмененной поликонической проекции, которая является произвольной.
В зависимости от вида нормальной сетки или способа построения картографической сетки проекции карт, используемых в самолетовождении, подразделяются на цилиндрические, конические, пол и конические, азимутальные и др. Нормальной называется такая сетка координатных линий, соответствующих определенной системе координат, которая имеет наиболее простое изображение в дайной проекции. В некоторых проекциях нормальная сетка совпадает с географической сеткой.
Цилиндрические проекции — это проекции, в которых меридианы нормальной сетки изображаются прямыми линиями, параллельными между собой и отстоящими друг от друга на расстояниях, пропорциональных разности соответствующих долгот; параллели изображаются в виде
прямых линий, перпендикулярных меридианам. Такая сетка получается при проектировании сетки меридианов и параллелей глобуса на боковую поверхность цилиндра (касательного или секущего) и развертывания этой поверхности па плоскость.
В зависимости от расположения оси цилиндра относительно оси вращения глобуса цилиндрические проекции делятся на нормальные цилиндрические проекции (ось цилиндра совпадает с осью вращения глобуса), поперечные цилиндрические проекции (ось цилиндра перпендикулярна оси вращения глобуса), косые цилиндрические проекции (угол между осью вращения цилиндра и осью глобуса больше 0 и меньше 90°).
В нормальных цилиндрических проекциях нормальная сетка совпадает с географической сеткой меридианов и параллелей.
Простая цилиндрическая проекция имеет следующие уравнения прямоугольных координат.
Вид географической сетки в простой цилиндрической проекции: меридианы — прямые, параллельные между собой и отстоящие друг от друга на расстояниях, пропорциональных разности Н долгот; параллели — прямые, перпендикулярные меридианам, отстоящие друг от друга на расстояниях, пропорциональных разности широт.
Проекция равнопромежуточна по направлениям меридианов. Все параллели (кроме экватора) искажены. Искажения в направлении параллелей увеличиваются при увеличении широты. На полюсе это искажение максимально, так как точки полюсов изображаются прямыми, длина которых равна длине экватора. Искажения углов и площадей также увеличиваются при увеличении широты. На полюсе искажение углов (2со) достигает 180°, а масштаб площади равен бесконечности.








 Летательные аппараты » Самолетовождение » Основы авиационной картографии » Ортодромия и локсодромия
Летательные аппараты » Самолетовождение » Основы авиационной картографии » Ортодромия и локсодромия