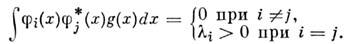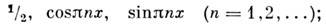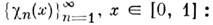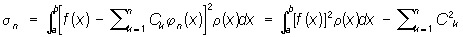Что такое ортогональные функции

ОРТОГОНАЛЬНАЯ СИСТЕМА ФУНКЦИЙ

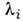
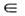
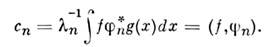
Ф-ция g(x )наз. весом О. с. ф.,* означает комплексное сопряжение. Если все = 1, то О. с. ф. наз. ортонормированной. О. с. ф. наз. полной, если длялюбой ф-ции f(x)L 2 (a,b )существует ряд Фурье сходящийся к f(х); такой ряд будет единственным, а его коэф. определяютсяф-лами Фурье
Всякая линейно независимая (полная) системаф-ций приводится с помощью процедуры ортогонализации (см. Ортонормированнаясистема векторов )к (полной) нормированной О. с. ф.
Для всякого ряда Фурье, построенного поО. с. ф.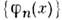, выполняется неравенство Бесселя

а для полной О. с. ф. справедливо равенствоПарсеваля

Примеры полных О. с. ф.:

2) системы ортогональных полиномов;

3)система Хаара

Полезное

Смотреть что такое «ОРТОГОНАЛЬНАЯ СИСТЕМА ФУНКЦИЙ» в других словарях:

Ортогональная система функций — система функций <(φn (x)>, n = 1, 2. ортогональных с весом ρ (х) на отрезке [а, b], т. е. таких, что Примеры. Тригонометрическая система 1, cos nx, sin nx; n = 1, 2. О. с. ф. с весом 1 на отрезке [ π, π]. Бесселя … Большая советская энциклопедия

ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О … Математическая энциклопедия

Полная система функций — такая система функций Ф = <φ(x:)>, определённых на отрезке [a, b], что не существует функции f (x), для которой, х) из Ф, т. е. для которой при любой функции φ(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл) … Большая советская энциклопедия

система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации

ПОЛНАЯ СИСТЕМА ФУНКЦИИ — см. в ст. Ортогональная система функций. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

ОРТОГОНАЛИЗАЦИЯ СИСТЕМЫ ФУНКЦИЙ — построение для заданной системы функций , интегрируемых с квадратом на отрезке [ а, Ъ]функций ортогональной системы путем применения нек рого процесса ортогонализации или же путем продолжения функций fn(x).на более длинный… … Математическая энциклопедия

Источник

Что такое ортогональные функции

В предыдущем разделе периодическая функция представлялась в виде разложения по синусам и косинусам. Почему мы не представляли эту функцию в виде ряда по периодическим функциям другого рода, например с помощью функции тангенс? Причина состоит в том, что синусы и косинусы обладают очень важным свойством – ортогональностью. Это означает, что средние значения произведений типа при осреднении за весь основной период Р равны нулю, за исключением случая, когда i=j. Далее, средние за период Р равны нулю для всех i и j.

Следствием ортогональности является то, что все коэффициенты упомянутых выше гармоник могут быть определены независимо друг от друга. Иначе говоря, чтобы найти, например, A₁ и B₁, не требовалось решать систему всех 12 уравнений для 12 величин A и В.

Существует еще другое следствие ортогональности синусов и косинусов. Пусть мы хотим описать временной ряд с помощью единственной гармоники с периодом Р, причем сделать это так, чтобы сумма квадратов отклонений между наблюдениями и синусоидальной кривой была бы минимальной. Как рассчитать такую кривую? Оказывается, что формулы для коэффициентов А и В для членов с синусом и косинусом соответственно будут точно такими же, как выражения для A₁ и B₁, применяемые в гармоническом анализе. Точно так же, если бы мы хотели определить наиболее подходящую синусоидальную кривую с периодом P/2 мы получили бы те же формулы, что для A₂ и B₂.

Фактически функции часто выбираются так, чтобы сумма их квадратов равнялась единице; в этом случае функции называются ортогональными и нормированными или сокращенно – ортонормированными. Функция

является примером ортонормированной функции.

Источник

Ортогональные функции

Две вещественные функции и на интервале называются ортогональными, если

Для комплексных функций вводится комплексное сопряжение одной из функций под интегралом, для векторных — скалярное произведение функций под интегралом, а также интегрирование по отрезку заменяется на интегрирование по области соответствующей размерности.

Полезным обобщением понятия ортогональности является ортогональность с определённым весом. Ортогональны с весом функции и , если

где — скалярное произведение векторов и — значений векторнозначных функций и в точке , — точка области , а — элемент её объёма (меры). Эта формула записана наиболее общим способом по сравнению со всеми выше. В случае вещественных скалярных , скалярное произведение следует заменить на обычное; в случае комплексных скалярных , : .

Пример

См. также

Полезное

Смотреть что такое «Ортогональные функции» в других словарях:

ортогональные функции — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN orthogonal functions … Справочник технического переводчика

ортогональные функции — ortogonaliosios funkcijos statusas T sritis fizika atitikmenys: angl. orthogonal functions vok. orthogonale Funktionen, f rus. ортогональные функции, f pranc. fonctions orthogonales, f … Fizikos terminų žodynas

Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия

ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — система многочленов <Р n (х)>, удовлетворяющих условию ортогональности причем степень каждого многочлена Р n (х). равна его индексу п, а весовая функция (вес) на интервале ( а, b).или (в случае конечности a и b) на отрезке [a, b]. О. м. наз. о р… … Математическая энциклопедия

Ортогональные многочлены — Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов … Википедия

ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — в комплексной области общее название многочленов, ортогональных на окружности, по контуру или по площади. В отличие от случая ортогональности в действительной области, многочлены указанных трех систем могут иметь мнимые коэффициенты и… … Математическая энциклопедия

Функции Ганкеля — (Ханкеля) (Функции Бесселя третьего рода) это линейные комбинации функций Бесселя первого и второго рода, а следовательно, решения уравнения Бесселя. Названы в честь немецкого математика Германа Ганкеля. функция Ганкеля первого рода; функция… … Википедия

Ортогональные многочлены — специальные системы многочленов <рп (х)>; n = 0, 1, 2. ортогональных с весом ρ(х) на отрезке [а, b ] (см. Ортогональная система функций). Нормированная система О. м. обозначается через х) удовлетворяет дифференциальному уравнению… … Большая советская энциклопедия

Бесселевы функции — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия

Источник

ортогональная система функций

Смотреть что такое «ортогональная система функций» в других словарях:

Ортогональная система функций — система функций <(φn (x)>, n = 1, 2. ортогональных с весом ρ (х) на отрезке [а, b], т. е. таких, что Примеры. Тригонометрическая система 1, cos nx, sin nx; n = 1, 2. О. с. ф. с весом 1 на отрезке [ π, π]. Бесселя … Большая советская энциклопедия

ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О … Математическая энциклопедия

Полная система функций — такая система функций Ф = <φ(x:)>, определённых на отрезке [a, b], что не существует функции f (x), для которой, х) из Ф, т. е. для которой при любой функции φ(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл) … Большая советская энциклопедия

система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации

ПОЛНАЯ СИСТЕМА ФУНКЦИИ — см. в ст. Ортогональная система функций. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

ОРТОГОНАЛИЗАЦИЯ СИСТЕМЫ ФУНКЦИЙ — построение для заданной системы функций , интегрируемых с квадратом на отрезке [ а, Ъ]функций ортогональной системы путем применения нек рого процесса ортогонализации или же путем продолжения функций fn(x).на более длинный… … Математическая энциклопедия

Источник

Ортогональная система функций

Полезное

Смотреть что такое «Ортогональная система функций» в других словарях:

ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О … Математическая энциклопедия

Полная система функций — такая система функций Ф = <φ(x:)>, определённых на отрезке [a, b], что не существует функции f (x), для которой, х) из Ф, т. е. для которой при любой функции φ(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл) … Большая советская энциклопедия

система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации

ПОЛНАЯ СИСТЕМА ФУНКЦИИ — см. в ст. Ортогональная система функций. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

ОРТОГОНАЛИЗАЦИЯ СИСТЕМЫ ФУНКЦИЙ — построение для заданной системы функций , интегрируемых с квадратом на отрезке [ а, Ъ]функций ортогональной системы путем применения нек рого процесса ортогонализации или же путем продолжения функций fn(x).на более длинный… … Математическая энциклопедия

Источник