Что такое ось симметрии 3 класс отрезок

Урок математики. Тема: «Ось симметрии»

Разделы: Математика

Перед каждым лежат ножницы и лист бумаги.

– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.

Вопрос: Какую функцию выполняет эта линия?

Предполагаемый ответ: Эта линия делит фигуру пополам.

Вопрос: Как расположены все точки фигуры на двух получившихся половинках?

Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.

– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.

– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.

– Начертить в тетради окружность.

Вопрос: Определить, как проходит ось симметрии?

Предполагаемый ответ: По-разному.

Вопрос: Так сколько осей симметрии имеет окружность?

Предполагаемый ответ: Много.

– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)

Вопрос: Какие еще фигуры имеют не одну ось симметрии?

Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.

– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?

Раздаю учащимся половинки фигурок из пластилина.

– Используя полученную информацию, долепить недостающую часть фигурки.

Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.

Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).

Задание 5 (групповая работа 5 мин).

– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.

Правильность выполненной работы определяется самими учениками.

Перед учащимися представлены элементы рисунков

– Найдите симметричные части этих рисунков.

Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:

1. Прямая ОР – ось симметрии треугольника КОМ.

Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?

2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.

3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.

– Наши первоначальные представления о форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях мало отличавшихся от жизни животных. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки, в которых обнаруживается замечательное чувство формы.
Когда произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, человечество вступает в новый каменный век, в неолит.
Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин, тканей, позже – обработка металлов вырабатывали представления о плоскостных и пространственных фигурах. Неолитические орнаменты радовали глаз, выявляя равенство и симметрию.
– А где в природе встречается симметрия?

Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…

– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.

Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.

1. Придумать свой орнамент, изобразить его на листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют элементы симметрии.

Источник

Симметрия

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

Вывод

Источник

Конспект урока по теме «Ось симметрии фигуры» 3 класс

Тема: Ось симметрии фигуры (2 урок)

Цель: упражнение в построении оси симметрии.

Задачи: 1. Создание условий для трансформации теоретических знаний в практические умения.

2. Формирование навыков самоконтроля, как способа действий через практическую проверку правильности проведения оси симметрии.

3. Обобщение представлений о геометрических фигурах через упражнение построения оси симметрии.

4. Формирование умения действия по алгоритму.

Материально-техническое оснащение: учебник С.С. Минаева, Л.О. Рослова, О.А.Рыдзе (2 часть), компьютер, проектор, презентация к уроку, канцтовары для практической работы (листы в клеточку, ножницы, линейка, карандаш), раздаточный материал (геометрические фигуры), наглядный материал (геометрические фигуры).

-Здравствуйте! Садитесь. Меня зовут Виктория Анатольевна. Сегодня я проведу у вас урок математики.

-Скажите, что на доске?

-Какое у них общее название?

-Откройте учебник на странице 90. В каком математическом разделе вы работали на прошлом уроке?

— Что нового вы узнали?

-Что такое ось симметрии?

-Замечательно. Осевая симметрия присуща всем формам в природе и является одним из основополагающих принципов красоты. Впервые обосновали понятие симметрии не только математики, а еще художники и философы Древней Греции. Древнегреческий философ Платон, живший в 429-327 годах до нашей эры, утверждал, что прекрасным может быть тот объект, который симметричен и соразмерен.

-На прошлом уроке вы познакомились с алгоритмом нахождения оси симметрии. Давайте его повторим.

— А теперь встанем и все вместе повторим алгоритм.

— Хорошо. Давайте выполним упражнение 254 на странице 92. Прочитайте задание.

Упражнение выполнять будем устно.

-Замечательно. Давайте выполним упражнения 252. Прочитайте задание.

-Выполните упражнение самостоятельно в тетради. На выполнение задания 3 минуты.

-Как вы проводили ось симметрии

Значит для того, чтобы провести ось симметрии у окружности, нужно провести ее через центральную точку.

Посмотрите у соседа по парте, там же у него проведена ось симметрии?

Но и у вас и у соседа тоже ось симметрии окружности, не смотря на то, что она в разных местах?

Какой вывод можно сделать? Сколько осей симметрии у окружности?

-Хорошо. Поработаем над упражнением 255. Прочитайте задание.

-Выполнять будем по рядам самостоятельно в тетради. 1 ряд – а); 2 ряд – б); 3 ряд – в). На выполнение задание 3 минуты.

-Напомните мне, что такое радиус?

-Чему равен радиус нашей окружности?

А что такое диаметр?

-Чему равен диаметр окружности?

-Какой из этих отрезков (радиус или диаметр) можно назвать осью симметрии? Почему?

-Мы с вами узнали, что у окружности бесконечное множество осей. Данный вывод можно отнести к другим фигурам?

Каждый ряд будет выполнять поиск осей симметрии у своей фигуры.

У вас на столе лежат конверты. В них листочки в клетку. Возьмите их и выполните на них задание. Фигуру надо нарисовать и вырезать. С помощью алгоритма выполнить поиск всех возможных осей симметрии.

Перед выполнением задания давайте вспомним правила безопасности при работе с ножницами.

Замечательно. Приступайте к работе.

1 ряд: сколько осей симметрии у вашей фигуры получилось?

У всех получилась одна?

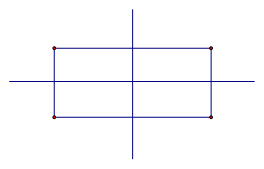
2ряд: сколько осей симметрии у прямоугольника?

У всех получилась две?

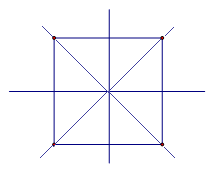
3ряд: сколько осей симметрии получилось у квадрата. Какие это оси?

Диагональ является осью симметрии?

-Сегодня мы с вами практическим путем узнали, что диагональ является осью симметрии.

-Как вы думаете, у всех ли треугольников одна ось симметрии?

У вас на столе лежит треугольник. Возьмите его и измерьте его стороны? Что вы заметили?

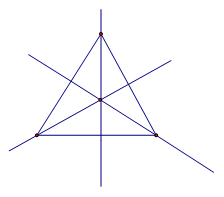
Это равносторонний треугольник. Давайте узнаем сколько у него осей симметрии.

Сколько осей симметрии вы нашли?

Треугольник оказывается сложная фигура. Есть еще много разных видов треугольников. Дома, если хотите, пробуйте найти их оси симметрии.

— А сейчас, давайте все вместе поработаем над упражнением 259. Прочитайте условие под буквой а).

Устно выполним задание.

Под буквой б) выполните дома.

-Замечательно. Давайте вспомним сколько осей симметрии у каждой фигуры мы сегодня нашли?

-Хорошо, а какой геометрической фигурой является поверхность парты?

-Сколько и какие оси симметрии у прямоугольника?

Дети, желаю вам никогда не проводить ось симметрии на парте, как разделительную полосу между соседом.

-В завершении сегодняшнего урока, прошу вас на листочках, которые лежат на вашем столе, закончить фразы. Подписывать листочки не нужно. После звонка сдайте их мне.

— Ось симметрии фигуры

— Что такое ось симметрии

Как построить ось симметрии

— Ось симметрии – это прямая линия, разделяющая фигуру на две равные части.

1.Перегнуть фигуру пополам.

2.Путем прижима зафиксировать линию сгиба.

3. Развернуть фигуру.

4. Провести прямую линию.

Дети встают и повторяют.

Ученик читает задание к упражнению.

Дети отвечают, ответ проверяется на слайдах.

Ученик встает и доказывает, является ли линия ОК осью симметрии.

Ученик читает задание к упражнению.

Дети выполняют задание.

Дети отвечают (через центральную точку)

— У окружности бесконечное множество осей симметрии

Ученик читает задание к упражнению.

Дети выполняют задание.

-Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.

Диаметр, потому что диаметр делит круг на две равные симметричные части.

Дети практическим путем ищут оси симметрии у треугольника.

-Вертикальная и горизонтальная

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Конспект урока по теме «Ось симметрии фигуры». Второй урок в данной теме. Цель урока: упражнение в построении оси симметрии фигуры. К уроку потребуется:

учебник С.С. Минаева, Л.О. Рослова, О.А.Рыдзе(2 часть), компьютер, проектор, презентация к уроку, канцтовары для практической работы (листы в клеточку, ножницы, линейка, карандаш), раздаточный материал (геометрические фигуры), наглядный материал (геометрические фигуры).

Номер материала: ДБ-938065

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Петербургский Политех перевел студентов на дистанционку

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В МГУ заработала университетская квантовая сеть

Время чтения: 1 минута

НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием

Время чтения: 2 минуты

В Хабаровском крае введут уроки по вакцинации в некоторых школах и колледжах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Что называется осевой симметрией

Что такое осевая симметрия в геометрии

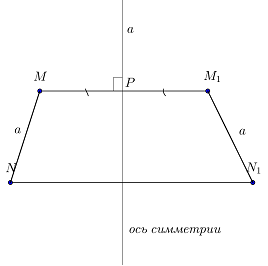
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – S_n, таким образом симметрия точек A и B обозначается так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

Теорема и доказательство

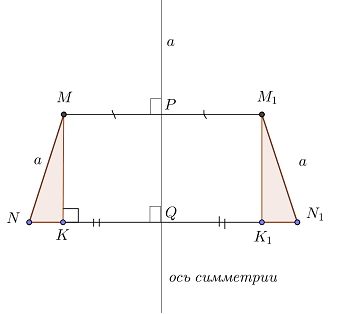
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.

Если отрезок MN симметричен отрезку M₁N₁ относительно прямой a, то MN = M₁N₁.

Чтобы доказать, что MN = M₁N₁, сделаем дополнительные построения:

Докажем, что прямоугольные треугольники MNK и M₁N₁K₁ равны. Стороны MN и M₁N₁ являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

Точка N отобразилась в точку N₁, значит:

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M₁N₁, что и требовалось доказать.

Фигуры, обладающие симметрией

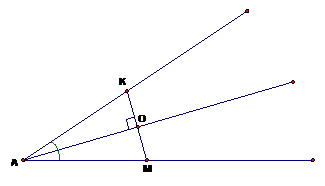
Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

Источник