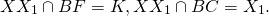Что такое ось симметрии 4 класс у треугольника равнобедренного треугольника
Симметрия в равнобедренном треугольнике
Есть ли симметрия в равнобедренном треугольнике? Сколько осей симметрии имеет равнобедренный треугольник? Есть ли в у равнобедренного треугольника центр симметрии?

Осью симметрии равнобедренного треугольника является прямая, перпендикулярная основанию и проходящая через его середину.
Пусть дан равнобедренный треугольник ABC с основанием AC.

В треугольнике ABC BF — высота и биссектриса, проведённые к основанию. По свойству равнобедренного треугольника BF является также его биссектрисой.
Отметим на стороне AB произвольную точку X.
Проведём из точки X прямую XX1, перпендикулярную BF,
Рассмотрим прямоугольные треугольники XBK и X1BK.
2) ∠XBK=∠X1BK (так как BF — биссектриса ∠ABC).
Следовательно, треугольники XBK и X1BK равны (по катету и острому углу).
Таким образом, точка, симметричная произвольной точке равнобедренного треугольника относительно прямой BF, также принадлежит этому треугольнику.
Точки B и F симметричны относительно прямой BF сами себе.
Следовательно, прямая прямая BF является осью симметрии треугольника ABC.
Центра симметрии равнобедренный треугольник не имеет.
Урок математики. Тема: «Ось симметрии»
Разделы: Математика
Перед каждым лежат ножницы и лист бумаги.
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
1. Прямая ОР – ось симметрии треугольника КОМ.
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях мало отличавшихся от жизни животных. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки, в которых обнаруживается замечательное чувство формы.
Когда произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, человечество вступает в новый каменный век, в неолит.
Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин, тканей, позже – обработка металлов вырабатывали представления о плоскостных и пространственных фигурах. Неолитические орнаменты радовали глаз, выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
1. Придумать свой орнамент, изобразить его на листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют элементы симметрии.
Презентация по математике «Оссевая симметрия»
Описание презентации по отдельным слайдам:
Двусторонняя симметрия — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны.
Посмотрите на снежинку, бабочку, листок. Что объединяет эти рисунки?
Если сложить пополам снежинку, бабочку, листок вдоль прямой, то её части совпадают.
Вокруг нас встречаются симметричные предметы. Если у предмета совпадают правая и левая сторона при сгибании, то такие предметы называются симметричными. Прямая, вдоль которой согнут предмет, называется осью симметрии
Если у предмета совпадают правая и левая сторона при сгибании,то такие предметы называются симметричными. Прямая, вдоль которой согнут предмет, называется осью симметрии
Если предметы симметричны относительно прямой (оси симметрии), то такая симметрия называется осевая симметрия
СИММЕТРИЯ В ПРИРОДЕ Prezentacii.com
Симметрия в природе Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.
Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
Симметрия у животных
Симметрия в животном мире.
Симметрия у растений
Издавна человек использовал симметрию в архитектуре
Волшебные загадки Зазеркалья Два кольца, два конца, А посередине – гвоздик. 1 Можно ли назвать ножницы симметричной фигурой? Почему?
Волшебные загадки Зазеркалья Хвост на дворе, Нос в конуре. Кто хвост повернёт, Тот и в дом войдёт 2 Можно ли назвать ключ симметричной фигурой? Почему?
Волшебные загадки Зазеркалья 3 Можно ли назвать стрекозу насекомым, у которого имеется ось симметрии? На ромашку у ворот Опустился вертолёт – Золотистые глаза. Кто же это.
Фигуры, обладающие осевой симметрией
Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
Фигуры, обладающие осевой симметрией
Квадрат, круг, равнобедренный треугольник – симметричные геометрические фигуры. Прямая, которая делит их на равные половины называется осью симметрии.
Практическая работа «5» «4»
Симметричные фигуры Несимметричные фигуры
Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии
Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии
Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии Параллелограмм Круг – бесконечное количество осей симметрии
Симметричные фигуры Несимметричные фигуры Прямоугольник – 2 оси симметрии Квадрат – 4 оси симметрии Параллелограмм
Найдите признак, по которому данные фигуры можно разбить на две группы. I группа (1, 4, 6) – фигуры, которые имеют две оси симметрии; II группа (2, 3, 5) – фигуры, которые имеют более двух осей симметрии. Что такое ось симметрии? Что такое ось симметрии?
Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
Буквы русского алфавита имеют оси симметрии А В Д Е Ж З К Л М Н О П С Т Ф Х Ш Э Ю
Существуют даже слова, имеющие ось симметрии МАДАМ КОК ФОКС НОС
Буквы, имеющие горизонтальную ось симметрии В Е Ж З К Н О С Ф Х Э Ю
Буквы, имеющие вертикальную ось симметрии А Д Ж Л М Н О П Т Ф Х Ш
Буквы, не имеющие ось симметрии Б Г И Р У Ц Ч Я Щ
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-804387
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
ЕГЭ в 2022 году пройдет в доковидном формате
Время чтения: 1 минута
Петербургский Политех перевел студентов на дистанционку
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Школьников Улан-Удэ перевели на удаленку из-за гриппа и ОРВИ
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Урок «Математика и конструирование» по теме «Осевая симметрия». 4-й класс
Класс: 4
Цель занятия: дать представление об осевой симметрии; научить находить осевую симметрию в фигурах.
Задачи:
Формируемые УУД:
Методическое оснащение: ПК, интерактивная доска, презентация, у каждого ученика: одна из геометрических фигур (квадрат, прямоугольник, равносторонний и прямоугольный треугольники, круг), линейка, ножницы, цветная бумага; карточки с заданиями.
Ход урока
1. Организационный момент
Добрый день, ребята. Мы начинаем урок «Математика и конструирование». Пусть сегодняшний урок принесёт нам радость общения. Сегодня на уроке вас ожидает много интересных заданий и новых открытий! А вашими помощниками пусть будут внимание, целеустремлённость и ваша активная деятельность.
2. Мотивирование к учебной деятельности
— А знаете ли вы, что …
— А знаете ли вы, что…
— Во время сна рост увеличивается на 8 мм. Но после пробуждения он «возвращается» к прежним цифрам.
— А знаете ли вы, что …
— А знаете ли вы, что …
— Число 111 111 магическое! При умножении его на само себя получается такой лёгкий ответ 12 345 654 321.
— А знаете ли вы, что …
— 90% информации человек получает при помощи глаз. Отсюда и пошло выражение «Лучше один раз …»
3. Актуализация знаний
— Посмотрите небольшой видео-ролик и найдите закономерность.
— Что интересного вы заметили? (отражение в воде)
— А где еще отражаются предметы? (В зеркале).
— Подумайте, как в математике называется зеркальное отображение? (СИММЕТРИЯ)
— Отлично! Сформулируйте тему урока. (или нам поможет ребус). (Слайд Симметрия.)
— Тогда Давайте поставим перед собой цель урока.
— Назовите предметы, которые вы считаете СИММЕТРИЧНЫМИ. (запись на доске) не знаем…, не уверенны…
— В переводе с греческого языка симметрия звучит как «гармония», означая красоту.
Симметрия придает гармоничность, законченность.
4. Практическая работа. Введение в новую тему «Ось симметрии»
Исследование квадрата.
— У вас на столе лежат квадраты.
— Сложите квадрат пополам и четко прогладим линию сгиба.
— Покажите! Что мы наблюдаете?
— Какие получились части квадрата? (Одинаковые)
— Обведите цветным карандашом получившуюся прямую. Это и есть ось симметрии!
Вывод: в квадрате мы нашли ось симметрии. Ось симметрии делит фигуру на одинаковые равные части. Эти половинки совпадают.
— Давайте попробуем сложить квадрат вновь пополам, но по-другому.
— Обведите эту линию.
— Как еще можно сложить квадрат? (по диагонали)
— Так сколько же осей симметрии у квадрата? (4)
— Правильно! Запишем это в таблицу
5. Физминутка (рисуем руками в воздухе)
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем 2 квадрата,
А на них огромный круг.
А потом ещё кружочек,
Треугольный колпачок.
Вот и вышел очень, очень
Развесёлый чудачок!
— Подойдите к окну, Пусть отдохнут ваши глаза, посмотрите по сторонам, полюбуйтесь красотой зимнего дня. Возможно, вы увидите симметричные предметы.…. Перечислите. Продолжаем работать!
6. Работа в группах
Исследование разных геометрических фигур. Защита.
— Каждый должен работать на общий результат.
— Один говорит, другие слушают.
— Своё несогласие высказывай вежливо.
Ваша задача узнать, симметрична ли фигура? сколько осей симметрии имеет геом. фигура? Выступать будет один представитель от группы. Вам дается 1 мин на исследование. И 1 мин на выступление. Используете алгоритм для выступления №1. (и демонстрирует на большой фигуре.)
— Возьмите фигуры из конверта. Приступайте к исследованию.
— Что нужно сделать, чтобы провести ось симметрии? (перегнуть фигуры пополам)
— Проведите оси симметрии, если это возможно. Цветным карандашом.
— Слушаем представителя 1-й группы.
— Приглашаем представителя 2-й группы.
— Слушаем представителя 3-й группы.
— Слушаем представителя 4-й группы. (На доске заполняю результаты исследований в таблице)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 1 ЗАДАНИЕМ.
— Назовите самую «несимметричную» фигуру. (Прям. Треугольник)
— Назовите самую «симметричную» фигуру. (круг)
— В Древней Греции круг считался венцом совершенства. И не случайно! У него больше всего осей симметрий!
7. Исследование в разных областях. Защита
— Мы выяснили, что в математике, не у всех фигур, но симметрия существует. Только ли в этой области она может быть?
— Оказывается, все в мире, всё построено по принципу симметрии. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. Используя красоту и гармонию природы, человек многое создал в мире симметрии своими руками. Об этих и многих других предметах мы сейчас и поговорим.
— Продолжим нашу исследовательскую работу.
— Возьмите конверт №2. Ознакомьтесь с темой исследования.
Приступайте к работе. Защита по алгоритму.
(Выступления групп. Выводы. Заполнение таблицы на доске.)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 2 ЗАДАНИЕМ.
— Итак, мы доказали, что Симметрия- это не только красота. Симметричность формы нужна рыбе, чтобы плыть, птице, чтобы летать. Поэтому мы можем сделать вывод, что симметрия в природе неспроста: она ещё и полезна, т.е. целесообразна.
— К какой области можно отнести эти предметы, созданные руками человека?
8. Подведение итогов «Кластер». Оценивание
— Какие цели мы ставили в начале урока? …(Что такое симметрия? Где встречается?)
— Что вы выяснили для себя?
— Какие слова, словосочетания, связи, явления события … и т.д. возникают с этой темой?
Домашнее задание
— Ребята, это не все ОБЛАСТИ, где ВСТРЕЧАЕТСЯ СИММЕТРИЯ. Подумайте дома, подготовьте картинку, в какой области можно встретить симметрию. (Спорт, искусство,…и т.д.)
— Символом симметрии является БАБОЧКА.
Я предлагаю вам создать уникальный узор на крыльях бабочки или выполнить другой симметричный рисунок на выбор. Подойдите, возьмите, что вам больше нравится.
— Рассмотрите иллюстрацию к мультфильму. Что увидел Енот в пруду?
— А можно ли проверить, доказать, СИММЕТРИЧНЫ ли предметы из повседневной жизни, крупные, твёрдые… НЕ бумажные.
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.