Что такое ось симметрии прямоугольника 3 класс математика

Прямоугольник. Ось симметрии фигуры

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

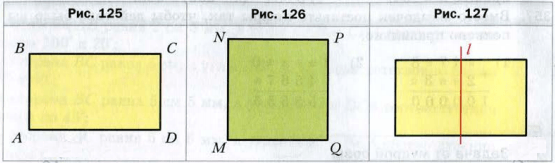
На рисунке 125 изображен прямоугольник ABCD.

Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны BC и CD.

Соседние стороны прямоугольника называют его длиной и шириной.

Стороны AB и CD не имеют общих вершин. Их называют противоположными сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.

Противолежащие стороны прямоугольника равны.

На рисунке 125 AB = CD, BC = AD. Если длина прямоугольника равна a, а ширина − b, то его периметр вычисляют по уже знакомой тебе формуле:

P = 2 a + 2 b

Прямоугольник, у которого все стороны равны, называют квадратом (рис. 126 ).

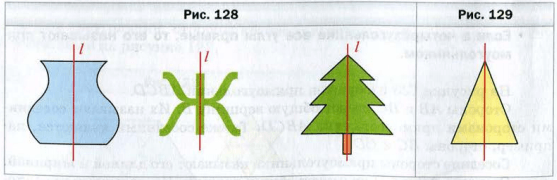
Проведем прямую l, проходящую через середины двух противолежащих сторон прямоугольника (рис. 127 ). Если лист бумаги перегнуть по прямой l, то две части прямоугольника, лежащие по разные стороны от прямой l, совпадут.

Итак, прямоугольник − это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник (рис. 129 ).

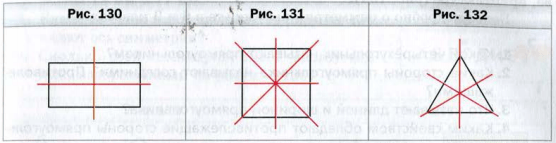
Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии (рис. 130 ), а квадрат − четыре оси симметрии (рис. 131 ). Равносторонний треугольник имеет три оси симметрии (рис. 132 ).

Объекты, имеющие ось симметрии, легко воспринимаются и приятные для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».

Идея симметрии широко используется в изобразительном искусстве, архитектуре (рис. 134 ).

Источник

Симметрия

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

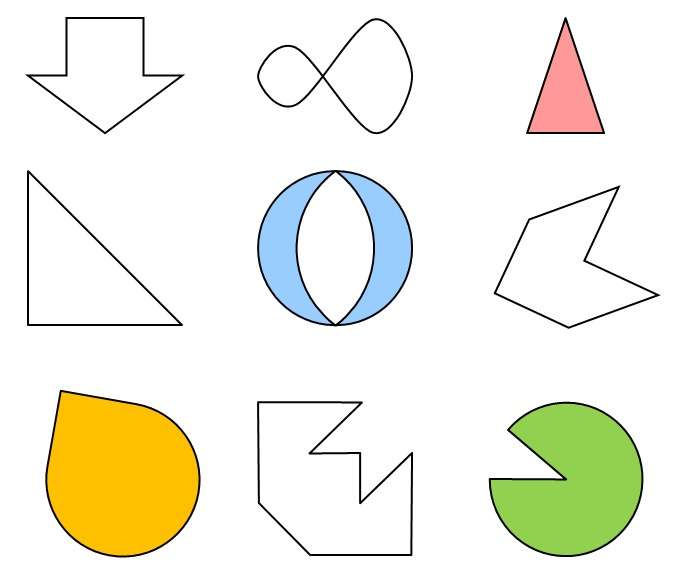
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

Вывод

Источник

Прямоугольник. Ось симметрии фигуры

Выбранный для просмотра документ Прямоугольник. Ось симметрии фигуры.docx

Технологическая карта урока – Прямоугольник. Ось симметрии фигуры.

Тип урока: комбинированный

Учитель: Санаева И.В.

Предметные: закрепить навыки распознавания, построения прямоугольника и квадрата, нахождение их периметров, научить учащихся находить на рисунках фигуры, имеющие ось симметрии, и в окружающем мире объекты, имеющие ось симметрии.

Личностные: формировать умение корректировать свои действия в соответствии с изменяющейся ситуацией.

Метапредметные: развивать познавательный интерес к математике, умение использовать приобретенные знания в практической деятельности.

Образовательные ресурсы: учебники, мультимедийная презентация, раздаточный материал

Применяемая технология : технология системно-деятельностного метода обучения

— словесные методы (беседа, чтение),

— наглядные (демонстрация презентации),

— метод рефлексивной самоорганизации (деятельностный метод).

— карточки с заданиями,

— карточки оценки работы на уроке,

— карточки с практическими заданиями по новой теме.

Формы организации познавательной деятельности:

Технологическая карта урока:

Он пройдёт ребятам впрок

Постарайтесь всё понять

Учитесь тайны открывать

Ответы полные давайте

И на уроке не зевайте.

Мы сегодня будем снова на раскрывать тайны математики

Приветствует обучающихся, проверяет их готовность к уроку

Приветствуют учителя проверяют свою готовность к уроку

2. Актуализация знаний.

постановка темы урока

-Что изучали на прошлом уроке? (вопросы по теме «Прямоугольник, квадрат»)

-Вопросы по домашней работе?

А если фигура будет уже дана, как найти площадь и периметр?

Возьмём прямоугольник соединим его противоположные вершины, свернём. Что получим?

Соединим его середины противоположных сторон. Что получим?

*перегиб листа, вырезание нарисованной на одной стороне фигуры;

*разглаживание линии сгиба и демонстрация всем, что получилось

*как расположились фигуры относительно линии сгиба

Давайте подумаем, о чем будет наш урок?

-Какую цель мы поставим?

-Сегодня мы будем работать по плану.

Что такое симметрия.

Что такое ось симметрии

Где встречается симметрия в окружающем нас мире.

В древности слово «симметрия» употреблялось как «красота», «гармония». Термин «гармония» в переводе с греческого означает «соразмерность, одинаковость в расположении частей». Известный немецкий математик нашего столетия Герман Вейль дал определение симметрии таким образом: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».

Активизировать мыслительные операции, внимание, память и т.д., стимулировать к активной работе

Учитель цитирует слова великого математика

-актуализируют знания прошлых уроков

-работают над понятиями

Учащиеся осмысливают сказанное

3. «Открытие» нового знания

Посмотрим внимательно на рисунки (рис. 1 и 2). Что вы на них увидели?

*перегиб листа,вырезание нарисованной на одной стороне фигуры;

*разглаживание линии сгиба и демонстрация всем, что получилось

*как расположились фигуры относительно линии сгиба

Построить процесс осознанного представления об осевой симметрии

— перегибают лист бумаги,вырезают-3

-наблюдение над фигурами относительно линии сгиба

— Сложим его пополам и четко обозначим линию сгиба.

— Что мы получили? Покажите!

— Обведём цветным карандашом получившуюся прямую. Это 1 ось симметрии.

— Давайте попробуем сложить квадрат вновь пополам, но по-другому.

— Как еще можно сложить квадрат?

— Так сколько же осей симметрии у квадрата? (4)

Активная работа н уроке 1 бал

Находят ось симметрии

4. Первичное закрепление

Цель: усвоение нового способа действий

Найти у фигур оси симметрии и заполнить таблицу (на столах лежат конверты(прямоугольник, квадрат, круг, равнобедренный и разносторонний треугольники, семиугольник)

Контролирует выполнение работы, оказывает помощь

Все правильно – 3 бала

Есть 2- 3 ошибки – 2 бала

Есть 4-5 ошибок – 1 бал

работают в парах, извлекают информацию

-принимают решение о возможности или невозможности проведения оси симметрии

5. Включение в систему знаний и повторение

Цель: включение «открытия» в систему знаний, повторения и закрепление ранее изученного

— Мы выяснили, что симметрия в математике существует, но не у всех фигур.

Только ли в этой науке она может быть?

Симметрия может встречаться не только в указанных группах, но и в другой окружающей нас действительности.

— Оказывается, все в мире построено по принципу симметрии. Продолжим нашу исследовательскую работу.

— Посмотрите, сколько областей жизни, и где только не встречается симметрия!

Знакомство с симметрией вокруг нас.

Организует исследовательскую работу

бала – работал активнее всех, предлагал интересные идеи.

2 бала – принимал активное участие в группе

1 бал – работал по мере необходимости

По ходу работы учитель составляет таблицу на доске:

(прикрепляют возле стрелочек свои проекты, некоторые стрелочки остаются пустыми.)

-Давайте сделаем вывод (по таблице).

-выполнение задания, основанного на ранее изученном

Выполняют исследовательскую работу в группе.

Покажите ребята свои рисунки. Итак, ребята, оцените себя:

3 бала – достроили все рисунки

2 бала- достроено 4 рисунка

1 бал – достроено 2 рисунка.

Создает ситуации успеха

3бала – работа оригинальная, аккуратная

2 бала – работа аккуратная, но рисунок простой

1 бал – работа не аккуратная

1.на уроке я работал…. активно/пассивно

2.своей работой на уроке я доволен /не доволен

3.Урок для меня показался… интересен/скучен

4.За урок я… не устал/устал

5.мое настроение… стало лучше/ хуже

6.материал урока мне был… понятен/не понятен

-учащиеся оценивают свою деятельность

-обозначают проблемные места

П. 15, №364, нарисовать фигуры имеющие ось симметрии (1,2 и более)

Какое открытие мы сделали на уроке?

— На следующем уроке мы будем учиться строить с вами симметричные геометрические фигуры относительно оси симметрии при помощи чертежных инструментов.

Что сегодня нового вы узнали? Что такое ось симметрии?

Сколько осей симметрии может иметь фигура?

8-9 балов – оценка 5

6-7 балов – оценка 4

Задает вопросы, корректирует ответы

8-9 балов – оценка 5

6-7 балов – оценка 4

Отвечают на вопросы

НАБОР ГЕОМЕТРИЧЕСКИХ ФИГУР

1 группа. Симметрия в мире животных.

На белой бумаге перед вами – контур бабочки. Проведите ось симметрии, раскрасьте бабочку в соответствии с правилами симметрии.

Определить оси симметрии у данных животных.

Правила работы в группе

1.Соответствует ли результат теме проекта.
2. Сотрудничество.
3. Аккуратность выполнения.
4. Защита проекта (умение донести информацию до аудитории).

2 группа. Симметрия в мире растений.

Перед вами – одна половинка известного всем растения, вторая его половинка рассыпалась в виде мозаики. Склейте растение и проведите оси симметрии.

Определить оси симметрии у данных растений.

Правила работы в группе

1.Соответствует ли результат теме проекта.
2. Сотрудничество.
3. Аккуратность выполнения.
4. Защита проекта (умение донести информацию до аудитории).

3 группа. Симметрия в мире архитектуры.

Построить с учетом воображаемой линии симметрии необычный замок, в котором вам хотелось бы жить.

Определить оси симметрии у данных памятников архитектуры.

Правила работы в группе

1.Соответствует ли результат теме проекта.
2. Сотрудничество.
3. Аккуратность выполнения.
4. Защита проекта (умение донести информацию до

Выбранный для просмотра документ симметрия.ppt

Описание презентации по отдельным слайдам:

Устный счет (42:6+14):3 (15*2+8) :2 81: 9*5 (24:8+7)*7 (48:3+4)*5 (77:11+13) :10 (15*3+5):2 =7 =19 =45 =70 =100 =2 =25

Прямоугольник A B C D S=a•b a b

Квадрат P=4•а а а а а S=a•a

Прямоугольник. Ось симметрии фигуры

Решить из учебника №359 №361 №363 №369

D A B C l Если через середины противолежащих сторон провести прямую и сложить по ней прямоугольник противоположными сторонами, то они совпадут Полученная прямая называется ось симметрии прямоугольника

Домашнее задание §15 №360 №362 №370

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-991167

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования

Время чтения: 2 минуты

Петербургский Политех перевел студентов на дистанционку

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Костромская область разработала программу привлечения педагогических кадров

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Прямоугольник. Ось симметрии фигуры

Урок 15. Математика 5 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямоугольник. Ось симметрии фигуры»

Давайте представим себе такую историю.

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Папа научил меня делать самолётик оригами! – восхищался Саша. – Посмотри, как круто летает такой самолётик!

– Да… его полёт завораживает! – наблюдал за самолётиком Паша. – Только вот я бы уточнил, что искусство создания бумажных самолётиков называется аэрогами или бумажная авиация. Это одна из техник оригами, при которой необходимо не только сложить красивую фигурку, похожую на оригинал, но и предусмотреть её лётные характеристики. Самолёты из бумаги были известны более 2000 лет назад. Однако тогда это были не самолётики, а птички.

Датой создания бумажного самолётика считается 1909 год, но более популярной датой является 1930 год. Тогда основатель известной компании по аэродинамике Lockheed Corporation Джек Нортроп заинтересовался, как из бумаги сделать самолёт.

– А зачем этому человеку нужны были бумажные самолётики? – поинтересовался Паша.

– Изобретатель хотел протестировать на бумажных самолётах свои новые идеи, – продолжил Паша. – Использование бумажной подделки в воздухе помогало правильно подбирать форму для будущих летательных аппаратов.

– Как же это интересно! – с восторгом сказал Саша.

– И это ещё не всё! – продолжил Паша. – В наши дни бумажная авиация, или аэрогами, получила мировую известность. Каждый человек знает, как сложить элементарный самолётик и запустить его. Но на сегодняшний день это уже не просто забава, а серьёзное увлечение, по которому проводят соревнования по всему миру.

– Вот бы мне побывать на таких соревнованиях, – сказал Саша.

– Обязательно побываешь! – подбодрил друга Паша. – Главное верить в свою мечту! Ну и, конечно же, тебе ещё будет полезным познакомиться с условиями создания и схемами бумажных самолётиков. Одними из главных условий создания самолётика являются использование бумаги прямоугольной или квадратной формы и чёткое соблюдение симметрии.

– Ого! – задумался Саша. – Вот про прямоугольные и квадратные формы я всё знаю, а про симметрию совсем ничего, – расстроился он.

– А давай спросим у Электроши, – предложил Паша. – Он точно всё знает!

– Ребята, прежде чем я вам расскажу о прямоугольниках и симметрии, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь поговорим о прямоугольниках, – предложил Электроша. – И сразу начнём с вопроса: как вы понимаете, что такое прямоугольник?

– Прямоугольник – это четырёхугольник, у которого все углы прямые, – ответил Паша.

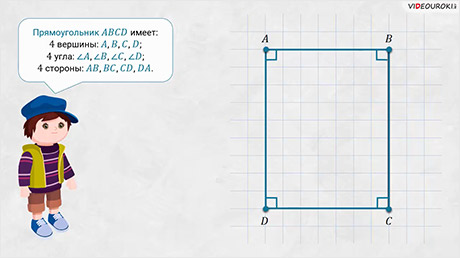
– Молодец! – похвалил Пашу Электроша. – Посмотрите: на листе изображён прямоугольник ABCD. Вы уже знакомы с элементами многоугольников. Назовите элементы нашего прямоугольника.

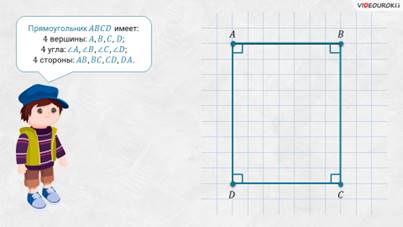
– Прямоугольник ABCD имеет 4 вершины: А, B, C и D, 4 одноимённых угла и 4 стороны: AB, BC, CD и DA – ответил Саша.

– Всё верно! – подтвердил Электроша. – Посмотрите: стороны AB и BC имеют общую вершину B. Такие стороны называют соседними сторонами прямоугольника ABCD. Также соседними сторонами будут стороны BC и CD с общей вершиной C, CD и DA с общей вершиной D, DA и AB с общей вершиной А.

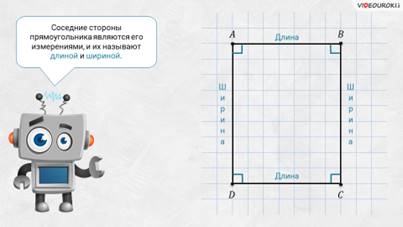
Соседние стороны прямоугольника являются его измерениями, и их называют длиной и шириной.

– А что вы можете сказать о сторонах, например, AB и CD нашего прямоугольника ABCD? – спросил у ребят Электроша.

– Стороны AB и CD не имеют общих вершин, – ответили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Такие стороны называют противолежащими сторонами прямоугольника ABCD. Также противолежащими будут стороны BC и AD. Запомните! Противолежащие стороны прямоугольника равны.

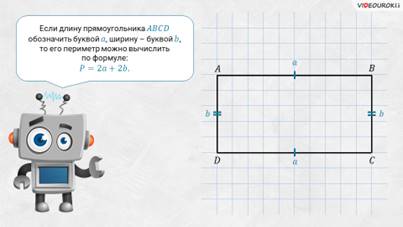
– А теперь посмотрите: на листке изображён прямоугольник ABCD, его противолежащие стороны равны. Если длину прямоугольника обозначить буквой а, а ширину – буквой b, то его периметр можно вычислить по формуле: P = 2a + 2b.

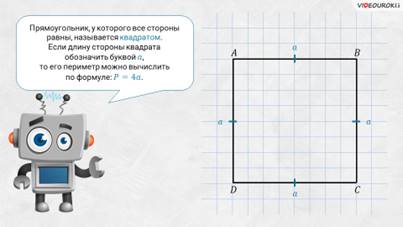
– Среди прямоугольников есть особые, – продолжил Электроша, – у которых все стороны имеют одну и ту же длину. Вы, конечно, помните, что такие прямоугольники называют квадратами. Если длину стороны квадрата обозначить буквой а, то его периметр можно вычислить по формуле: P = 4a.

– А теперь давайте проведём небольшой эксперимент. Возьмите лист бумаги прямоугольной формы и сложите его пополам так, чтобы противолежащие стороны совпали. Затем разверните этот лист. Что вы можете сказать о двух частях, получившихся в результате сгиба листа? – спросил у ребят Электроша.

– Видно, что две части нашего прямоугольного листа, лежащие по разные стороны от линии сгиба, совпадают.

– Молодцы! – похвалил ребят Электроша. – Прямую, которую мы получили в результате сгибания листа, называют осью симметрии.

Запомните! Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры. Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.

– Скажите, сколько осей симметрии имеет прямоугольник? – спросил Электроша.

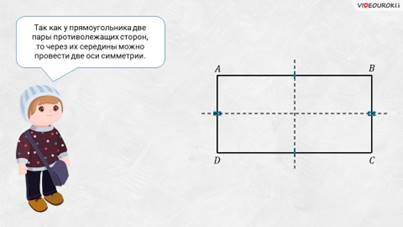
– Так как у прямоугольника 2 пары противолежащих сторон, то через их середины можно провести 2 оси симметрии, – сказал Паша.

– Правильно! А, может, вы ещё сможете привести примеры симметричных фигур в геометрии?

– Например, квадрат, – начал Саша. – У квадрата тоже 2 пары противолежащих сторон, значит, через их середины можно провести 2 оси симметрии.

– Саша, ты чуть-чуть не досчитался! – сказал Электроша. – Вы уже знакомы с таким понятием, как диагональ. Напомню, что диагональ – это отрезок, соединяющий любые две несоседние вершины.

Если лист квадратной формы сложить пополам по диагоналям, то заметим, что и эти пары частей совпадут относительно линий сгиба.

– Значит, у квадрата 4 оси симметрии? – уточнил Саша.

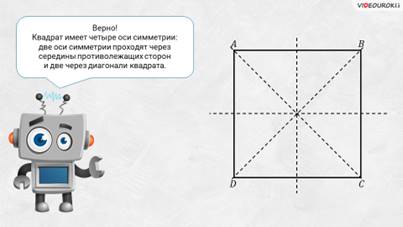
– Верно! – ответил Электроша – Квадрат имеет 4 оси симметрии: 2 оси симметрии проходят через середины противолежащих сторон и 2 – через диагонали квадрата.

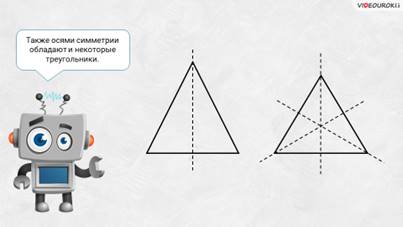
Также осями симметрии обладают и некоторые треугольники. Так, например, в равнобедренном треугольнике можно провести 1 ось симметрии, а в равностороннем – 3.

– С симметрией вы очень часто встречаетесь и в жизни. Люди с давних времён используют симметрию в рисунках, орнаментах, предметах быта, архитектуре, искусстве.

Даже многие буквы нашего алфавита обладают симметрией.

Однако больше всего восхищает симметрия в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, окраске и расположении различных органов животных, в форме кристаллических тел.

В порхающей бабочке и сказочной зимней снежинке.

Объекты, которые обладают осью симметрии, всегда легко воспринимаются и приятны для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». Симметрия означает соразмерность, наличие определённого порядка в расположении частей.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

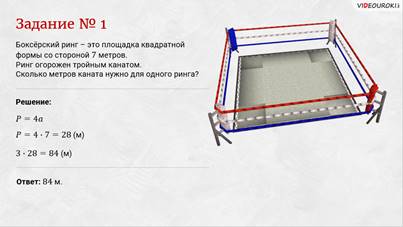
Задание первое: боксёрский ринг – это площадка квадратной формы со стороной 7 м. Ринг огорожен тройным канатом. Сколько метров каната нужно для одного ринга?

Решение: чтобы узнать, сколько понадобится метров каната для ринга, нужно знать периметр ринга. Мы знаем, что ринг имеет форму квадрата со стороной 7 м. Применяя формулу для вычисления периметра квадрата, получаем, что наш ринг имеет периметр 28 м. Так как ринг огорожен тройным канатом, то для одного ринга понадобится 84 метра каната.

Следующее задание: сколько осей симметрии имеет шестиугольник с равными сторонами?

Решение: так как, по условию, шестиугольник имеет равные стороны, а их 6, значит, можно провести 3 оси симметрии через середины противолежащих сторон. Также можно провести ещё 3 оси симметрии через диагонали шестиугольника. Тогда всего получим 6 осей симметрии.

Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры.

Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.

У прямоугольника 2 оси симметрии, у квадрата – 4, у равнобедренного треугольника – 1, а у равностороннего – 3.

Источник