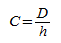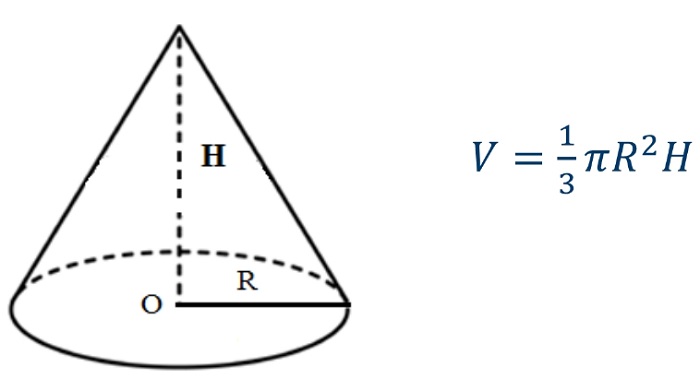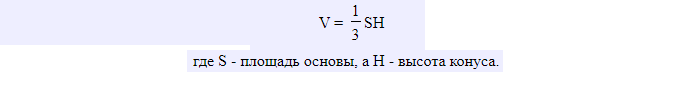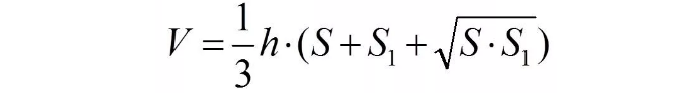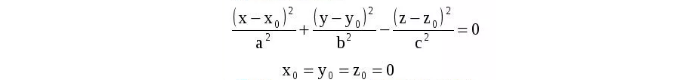Что такое основание конуса

Что такое конус: определение. Основание, вершина, высота конуса

Определение фигуры

Предположим, что имеется некоторая плоская замкнутая кривая, например окружность или эллипс. В пространстве выберем некоторую точку, которая не принадлежит плоскости указанной кривой. Теперь соединим ее с каждой точкой на кривой при помощи прямых отрезков. Полученная фигура дает ответ на вопрос о том, что такое конус. На фото ниже показаны три конуса, изготовленные из бумаги.

Вам будет интересно: Подберем рифму к слову «капля»

Исходная замкнутая кривая называется директрисой или направляющей фигуры. Фиксированная точка в пространстве, упомянутая выше, называется вершиной конуса. Прямые отрезки, которые соединяют вершину с точками на директрисе, получили название генератрис, или образующих.

Рассматриваемая фигура образует некоторую поверхность, поэтому объемом не обладает. Если же внутри эту фигуру заполнить каким-либо веществом, то у нее появится некоторый объем. Полученное твердое тело также называется конусом.

Элементы конуса

Вам будет интересно: Абашевская культура бронзового века: локализация, археологические находки

Под элементами фигуры понимают геометрические объекты, из которых она состоит. Зная, что такое конус, можно сказать, что основными его элементами являются следующие:

Виды конуса

Мы узнали, что такое конус. Теперь перейдем к рассмотрению вопроса о том, какие виды фигур бывают.

В зависимости от кривой, находящейся в основании, говорят о конусе круглом, эллиптическом, гиперболическом, параболическом и так далее. Кроме того, фигура может быть прямой и наклонной. Чтобы понять разницу между ними, следует познакомиться с понятием высоты.

В большинстве геометрических задач рассматривают прямой конус с круглым основанием. Далее в статье дадим подробную характеристику этой фигуре.

Как можно получить круглый прямой конус?

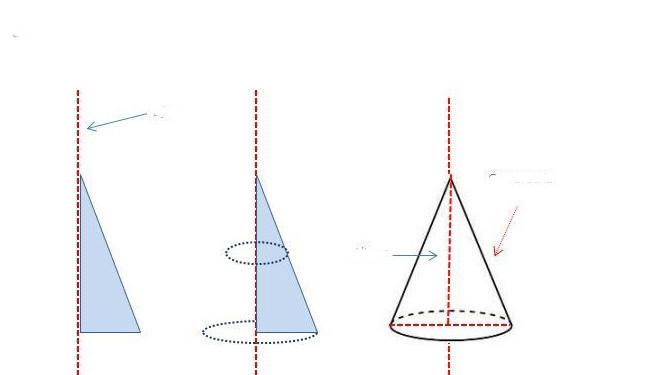
В результате описанного способа получения круглого конуса образуется фигура, имеющая радиус основания a и высоту b. Катет b является частью оси конуса, которая проходит через его вершину и центр основания. Гипотенуза исходного треугольника будет генератрисой фигуры.

Схема выше показывает, как можно получить конус, вращая прямоугольный треугольник вокруг одного из катетов.

Линейные характеристики круглого прямого конуса

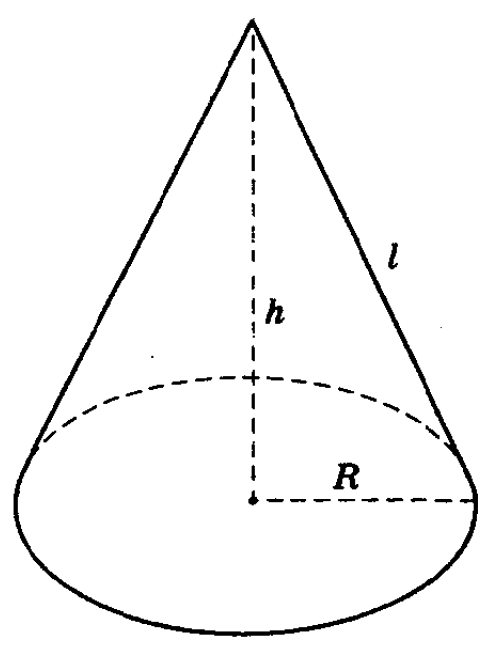
Фигура образована кругом некоторого радиуса r и конической поверхностью. Пусть высота конуса равна h. Указанные две линейные характеристики являются основными. Их знание позволяет вычислить любые параметры фигуры, например, длину его генератрис, площадь поверхности и объем.

Поскольку рассматриваемая фигура является прямой, то длины всех его генератрис равны между собой. Если обозначить их длину буквой d, тогда формула для ее вычисления будет иметь вид:

Нетрудно догадаться, откуда взялась эта формула. Она является результатом применения теоремы Пифагора к соответствующему прямоугольному треугольнику. Отметим, что генератриса конуса всегда больше радиуса его основания, независимо от значения величины h.

Данное выражение позволяет по двум известным линейным величинам определить третью. Например, если известны d и h, тогда радиус круга в основании будет равен:

Поверхность и объем

S = pi*r2 + pi*r*√(r2 + h2).

Объем конуса произвольного типа рассчитывается по следующей формуле:

Здесь символом So обозначена площадь основания. Заметим, что аналогичная формула и у объема пирамиды. Это совпадение не является случайным, поскольку увеличение числа граней пирамиды до бесконечности переводит ее в конус.

Записанная формула для случая прямого круглого конуса приобретает конкретный вид:

Здесь множитель pi*r2 является площадью основания (круга).

Таким образом, объем прямого конуса, основанием которого является круг, равен одной трети объема цилиндра, имеющего тот же радиус и ту же высоту.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Стереометрия:

Контакты

Конус

Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.

Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.

Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.

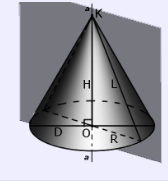
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.

Круговой конус — конус, у которого в основании круг.

Прямой круговой конус ( просто конус ) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

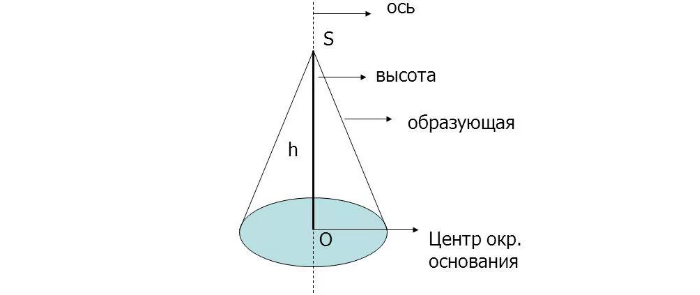
Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.

Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.

Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.

Образующие конуса совпадают с образующими конической поверхности.

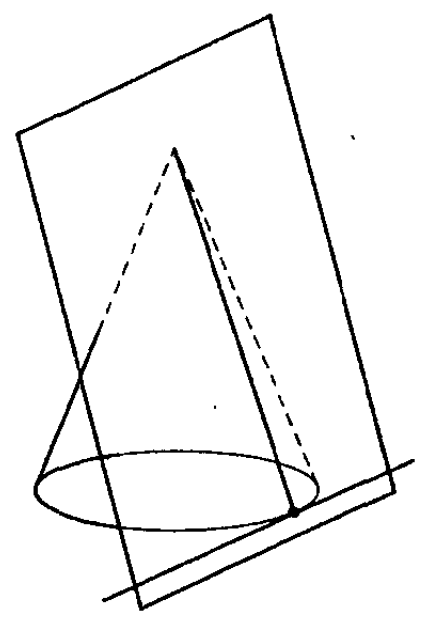
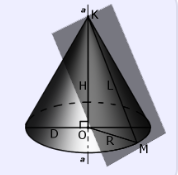
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. См.Рис.2.

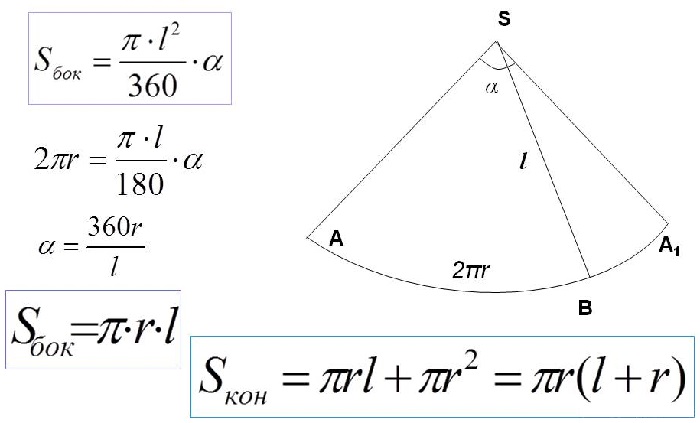
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

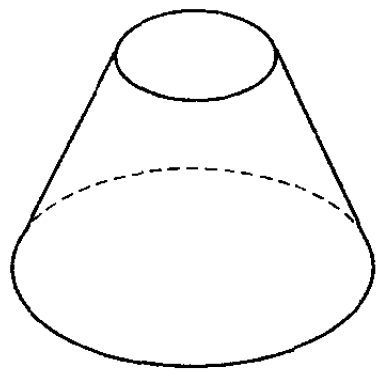
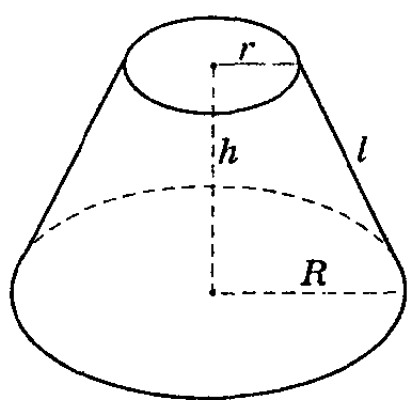
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3.

Видео-решение.

Инструменты страницы

Записаться на занятия

Источник

Что такое конус: определение, элементы, виды

В данной публикации мы рассмотрим определение, основные элементы и виды одной из самых распространенных фигур в пространстве – конуса. Представленная информация сопровождается соответствующими рисунками для лучшего восприятия.

Определение конуса

Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.

Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.

Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.

Основные элементы конуса

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.

Источник

С точки зрения геометрии речь идет о пространственной фигуре, которая образована совокупностью прямых отрезков, соединяющих некоторую точку пространства со всеми точками плавной плоской кривой. Этой кривой может быть окружность или эллипс. На рисунке ниже показан конус.

Вам будет интересно: Советские вещи: фото и описание

Представленная фигура не обладает объемом, поскольку стенки ее поверхности имеют бесконечно малую толщину. Однако если ее заполнить веществом и ограничить сверху не кривой, а плоской фигурой, например кругом, то мы получим твердое объемное тело, которое также принято называть конусом.

Форму конуса можно часто встретить в жизни. Так, ею обладает мороженое-рожок или полосатые черно-оранжевые дорожные конусы, которые выставляют на проезжую часть для привлечения внимания участников движения.

Элементы конуса и его виды

Поскольку конус полиэдром не является, то количество образующих его элементов не так велико, как для многогранников. В геометрии конус общего вида состоит из следующих элементов:

Заметим, что вершина в плоскости основания не должна лежать, поскольку в этом случае конус вырождается в плоскую фигуру.

Если из вершины провести перпендикулярный отрезок к основанию, то мы получим высоту фигуры. Если последняя основание пересекает в геометрическом центре, то это конус прямой. Если же перпендикуляр не совпадает с геометрическим центром основания, то фигура будет наклонной.

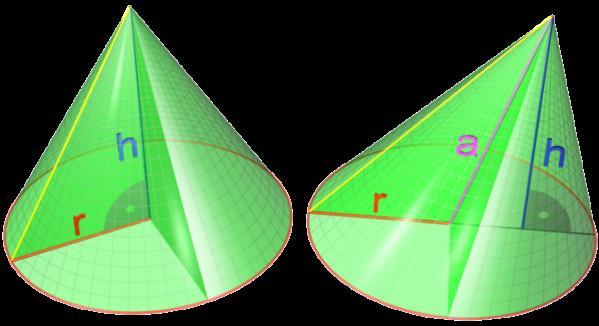
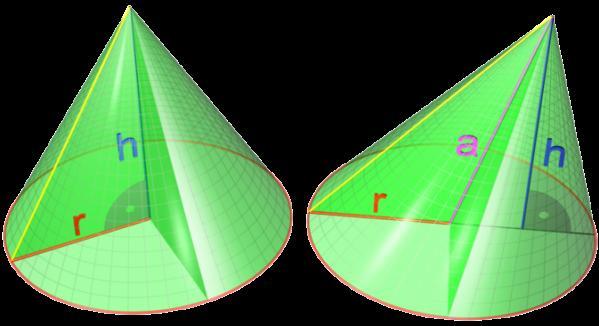
Прямой и наклонный конусы показаны на рисунке. Здесь высота и радиус основания конуса обозначены h и r соответственно. Линия, которая соединяет вершину фигуры и геометрический центр основания, является осью конуса. Из рисунка видно, что для прямой фигуры высота на этой оси лежит, а для наклонной фигуры высота с осью образует некоторый угол. Ось конуса обозначена буквой a.

Прямой конус с круглым основанием

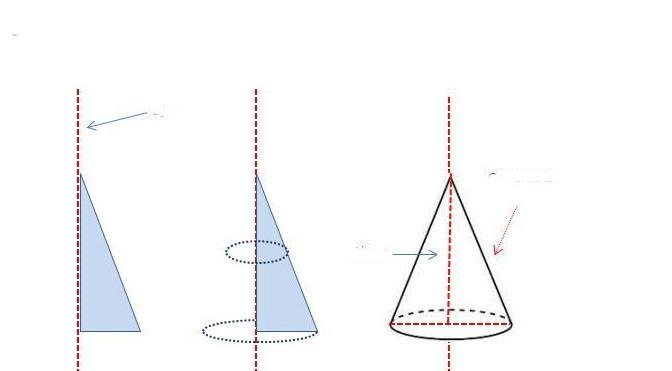
Пожалуй, это конус самый распространенный из рассматриваемого класса фигур. Состоит он из круга и боковой поверхности. Получить геометрическими методами его не представляет никакого труда. Для этого следует взять прямоугольный треугольник и вращать его вокруг оси, совпадающей с одним из катетов. Очевидно, что этот катет станет высотой фигуры, а длина второго катета треугольника образует радиус основания конуса. Схема ниже демонстрирует описанную схему получения рассматриваемой фигуры вращения.

Изображенный треугольник можно вращать вокруг другого катета, при этом получится конус с большим радиусом основания и меньшей высотой, чем первый.

Для однозначного определения всех параметров круглого прямого конуса следует знать любые две его линейных характеристики. Среди них выделяют радиус r, высоту h или длину генератрисы g. Все названные величины являются длинами сторон рассмотренного прямоугольного треугольника, поэтому для их связи справедлива теорема Пифагора:

Площадь поверхности

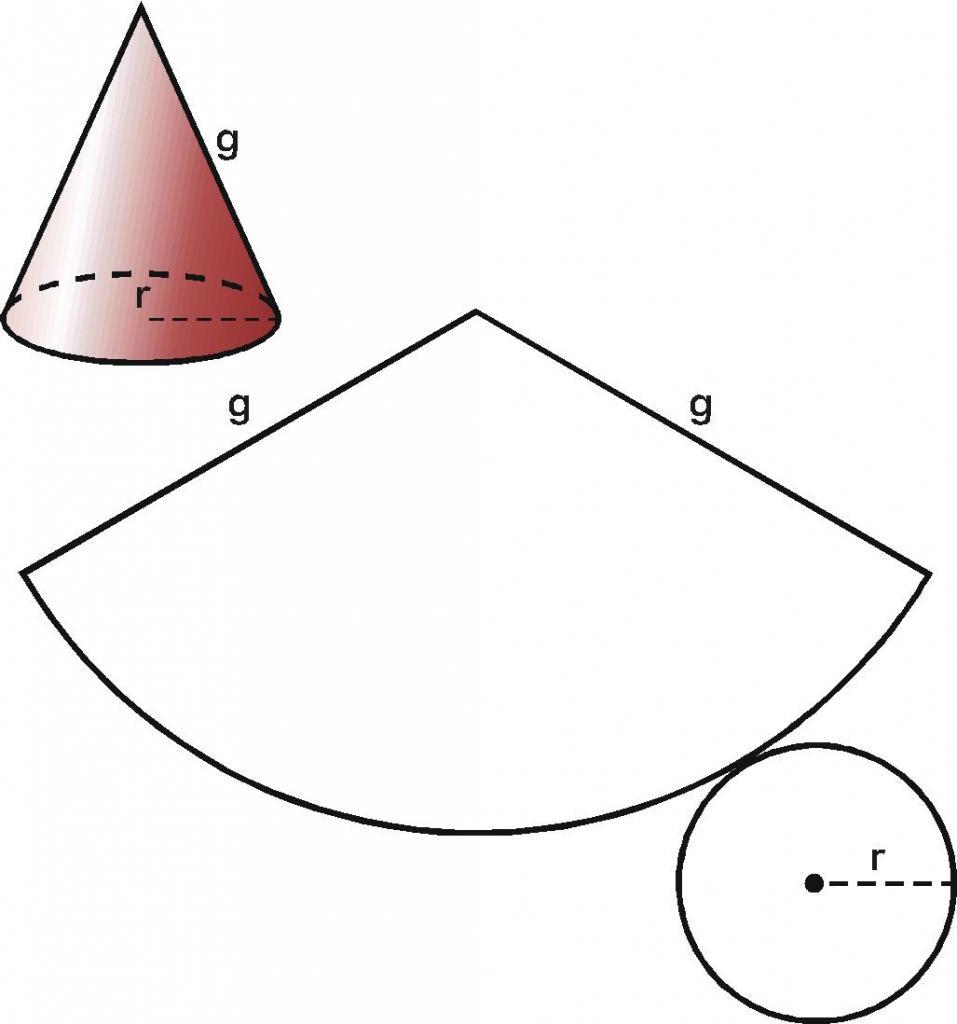
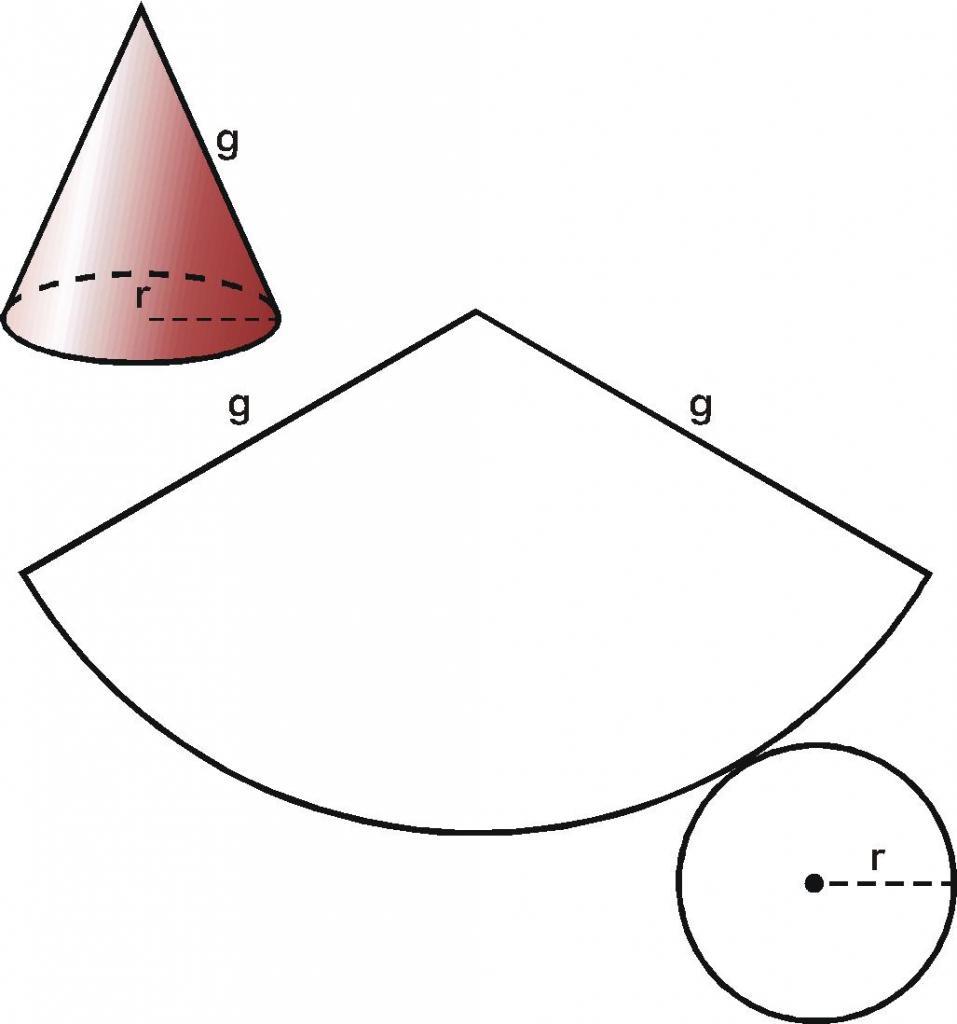
При изучении поверхности любой объемной фигуры удобно пользоваться ее разверткой на плоскость. Конус не является исключением. Для круглого конуса развертка показана ниже.

Мы видим, что развертка фигуры состоит из двух частей:

Площадь круга найти легко, и соответствующая формула известна каждому школьнику. Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:

Если длина генератрисы g неизвестна, но дана высота h фигуры, тогда формулу можно переписать в виде:

S = pi*r2 + pi*r*√(r2 + h2).

Объем фигуры

Если взять прямую пирамиду и увеличивать на бесконечности число сторон ее основания, то форма основания будет стремиться к окружности, а боковая поверхность пирамиды будет приближаться к конической поверхности. Эти рассуждения позволяют использовать формулу для объема пирамиды при расчете аналогичной величины для конуса. Объем конуса может быть найден по формуле:

Справедлива эта формула всегда, независимо от того, что собой представляет основание конуса, имеющее площадь So. Более того, формула применима также для наклонного конуса.

Поскольку мы изучаем свойства прямой фигуры с круглым основанием, то для определения его объема можно пользоваться таким выражением:

Справедливость формулы очевидна.

Задача на нахождение площади поверхности и объема

Пусть дан конус, радиус которого равен 10 см, а длина образующей составляет 20 см. Необходимо определить объем и площадь поверхности для этой фигуры.

Для вычисления площади S можно сразу воспользоваться формулой, записанной выше. Имеем:

S = pi*r2 + pi*r*g = 942 см2.

Для определения объема необходимо знать высоту h фигуры. Рассчитаем ее, пользуясь связью между линейными параметрами конуса. Получаем:

Теперь можно воспользоваться формулой для V:

V = 1/3*h*pi*r2 = 1/3*17,32*3,14*102 ≈ 1812,83 см3.

Отметим, что объем круглого конуса составляет третью часть от цилиндра, в который он вписан.

Источник

Из огромного перечня математических заданий часто встречаются задачи, связанные с темой «Конус». На уроках геометрии школьники должны усвоить основные понятия и названия всех элементов этой фигуры и понять, как и по каким формулам производится расчет нужных параметров.

О данной геометрической фигуре пойдёт речь в сегодняшней статье.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

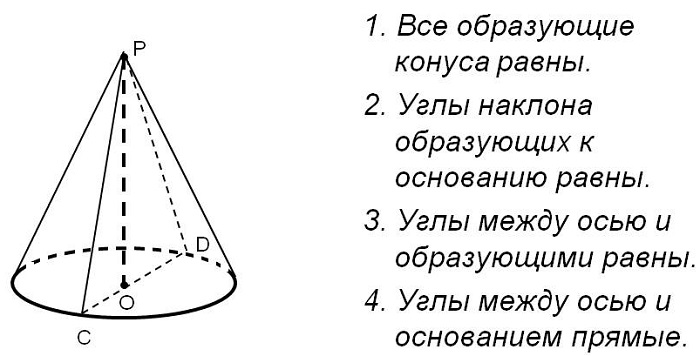
Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:

Образующие кругового конуса равны друг другу.

Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.

Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Общая формула объёма фигуры

Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

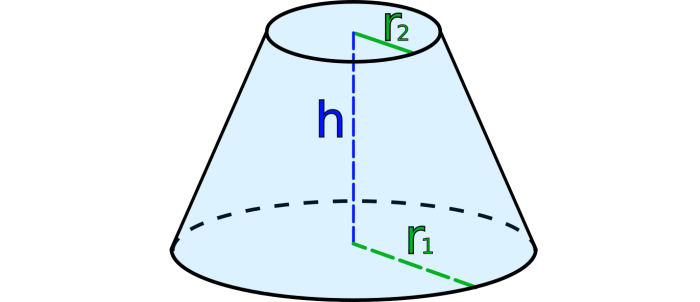
Объём усечённого конуса

Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

Объём данного тела можно вычислить по формуле:

Важно! S и S ₁ это площади соответствующих основ, которые равняются ПR 2 и ПR ₁ 2 При нахождении этих значений поможет онлайн калькулятор.

Площадь поверхности фигуры

Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

площади боковой поверхности усечённого конуса S_бок;

полной площади усечённой фигуры S_пол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

где x₀, y_0,z₀— координаты по соответствующим осям.

Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

Источник