Что такое основание перпендикуляра в геометрии

Значение словосочетания «основание перпендикуляра»

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова шредер (существительное):

Ассоциации к слову «основание&raquo

Ассоциации к слову «перпендикуляр&raquo

Синонимы к словосочетанию «основание перпендикуляра&raquo

Предложения со словом «основание&raquo

Предложения со словом «перпендикуляр&raquo

Цитаты из русской классики со словосочетанием «основание перпендикуляра»

Сочетаемость слова «основание&raquo

Афоризмы русских писателей со словом «основание&raquo

Отправить комментарий

Дополнительно

Предложения со словом «основание&raquo

Резонансное дело даёт основания полагать, что расстрелы членов партии были всё же явлением исключительным и единичным.

Эти работы дали основание считать его общепризнанным отцом географии.

– Теперь ты на всех законных основаниях являешься полновластным обладателем отличного нового папы.

Предложения со словом «перпендикуляр&raquo

Для определения суточных потребностей в воде и электролитах восстанавливают перпендикуляр от показателя возраста или массы больного до пересечения с неправильной кривой в средней части номограммы.

Это разметочный инструмент, который применяют для измерения длины на чертежах, деления углов, прямых линий для вычерчивания окружностей, построения перпендикуляров.

По центру поставим засечку и поднимем вверх перпендикуляр, на котором отложим длину юбки по боку.

Источник

Геометрия. 7 класс

Конспект урока

Перпендикуляр к прямой

Перечень рассматриваемых вопросов:

Теорема – утверждение, справедливость которого устанавливается путём рассуждений.

Отрезок – часть прямой, ограниченная двумя точками.

Перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Теоретический материал для самостоятельного изучения.

Пешеходный переход, так называемая «зебра», расположен под углом 90 градусов к улице. Выбор такого угла сделан не случайно. Ведь перейти дорогу пешеходам необходимо как можно быстрее. Такой путь оказывается самым коротким. Чтобы быстрее добраться от метро Площадь Восстания в Санкт-Петербурге до Набережной реки Фонтанки, необходимо идти по Невскому проспекту, перпендикулярно реке.

Ножки стола крепятся перпендикулярно столешнице. Маятник часов расположен перпендикулярно верхней стенке часов.

Если считать улицу, набережную реки Фонтанки, ребро столешницы, ребро стенки часов моделями прямых, то можно говорить, что на каждой картинке построены перпендикуляры к прямой.

Примеры с картой и пешеходным переходом иллюстрируют тот факт, что перпендикуляр к прямой – это кратчайший путь от точки до прямой. Такой путь называется расстоянием.

Пример с часами поможет нам запомнить происхождение слова перпендикуляр. В переводе с французского перпендикуляр означает висеть. То есть, перпендикуляр – это отвес.

Дадим определение перпендикуляра к прямой.

Мы знаем, что перпендикулярными прямыми называются две пересекающиеся прямые, которые образуют при пересечении четыре прямых угла.

Часть одной из этих прямых является перпендикуляром к прямой.

Выделенная часть прямой ограничена двумя точками, значит, по определению, – это отрезок. Один из концов этого отрезка является точкой пересечения перпендикуляра и прямой, к которой он проведен.

перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Н – основание перпендикуляра.

Предположим, что вы купаетесь в море недалеко от берега. Вдруг появилась акула, необходимо срочно плыть к берегу. Конечно, вы выберите самый короткий путь. А мы уже знаем, что в геометрии этот путь называют перпендикуляром к прямой.

Всегда ли можно найти кратчайший путь? Сколько существует способов построения кратчайшего пути?

Если на пути нет препятствий, например, здания, ямы, в данном примере – других пловцов, то самый короткий путь проделать можно. И такой путь единственный.

В геометрии любое утверждение требует доказательства. Сформулируем теорему о перпендикуляре к прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

По условию теоремы нам даны прямая и точка.

Заключение теоремы состоит из двух частей – существование перпендикуляра и его единственность.

1.Через точку А можно провести перпендикуляр к прямой BC.

2.Данный перпендикуляр единственный.

Разбор заданий тренировочного модуля.

Задание 1. Построить перпендикуляр к прямой.

Для этого можно использовать чертёжный угольник, одну сторону которого от угла в 90 градусов прикладываем к прямой, к которой проведём перпендикуляр из точки, не лежащей на этой прямой, а вторую сторону угольника совместим с точкой, от которой проведём перпендикуляр к прямой.

Задание 2. На рисунке изображены два перпендикуляра АB и СD к прямой а, при этом АB = СD.

Докажем, что треугольники ABD и CDВ равны.

По условию в треугольниках ABD и CDВ, сторона АBравна стороне СD.

AB ⊥ а =>∠ABD = 90° (по определению перпендикулярных прямых).

СD ⊥ а => ∠CDВ = 90° (по определению перпендикулярных прямых).

Следовательно, ∠ABD = ∠CDВ.

Следовательно, ∆ABD = ∆CDВ

(по первому признаку равенства треугольников: по двум сторонам и углу между ними).

Источник

Что такое основание перпендикуляра в геометрии

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №10. Перпендикуляр и наклонные

Перечень вопросов, рассматриваемых в теме.

Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.

Источник

Перпендикуляр и наклонная:

Рассмотрим понятия перпендикуляра и наклонной к прямой в плоскости.

Пусть точка О и прямая а лежат в плоскости, а точка О не лежит на прямой а.

Перпендикуляром, проведенным из точки О к прямой а, называется отрезок ОB, такой, что точка B лежит на прямой а и отрезок ОB перпендикулярен прямой а. Точка B называется основанием перпендикуляра.

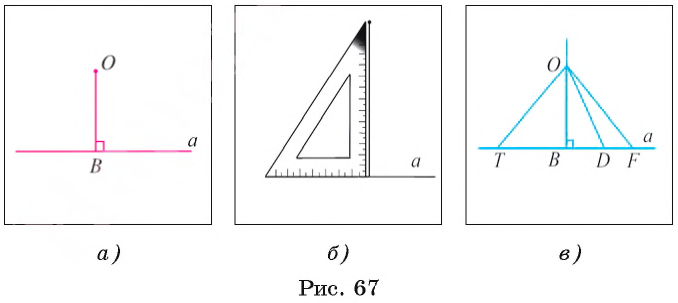
На рисунке 67, а отрезок ОB — перпендикуляр, проведенный из точки О к прямой а.

При изображении перпендикулярных прямых или перпендикуляра пользуются чертежным угольником (рис. 67, б).

Пусть точка B — основание перпендикуляра ОB, проведенного из точки О к прямой а.

Отрезок, соединяющий точку О с любой точкой прямой а, не совпадающей с основанием B перпендикуляра, называется наклонной к прямой а.

На рисунке 67, в изображены наклонные OF, OD и ОТ к прямой а.

Теорема 1 (о существовании единственного перпендикуляра, проведенного из точки к прямой).

Из точки, не лежащей на прямой в плоскости, можно провести единственный перпендикуляр к данной прямой.

1. Докажем, что такой перпендикуляр существует.

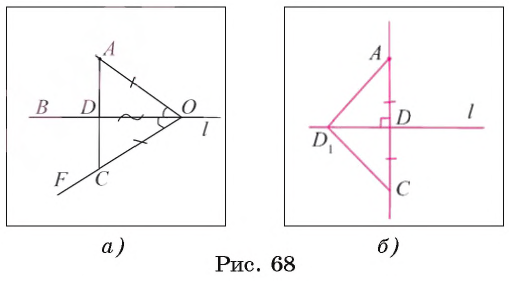
Пусть точка А не принадлежит прямой l. Возьмем на этой прямой некоторую точку О и проведем луч ОА (рис. 68, а). Далее от луча OB в другой полуплоскости отложим угол BOF, равный углу АОВ. На луче OF отложим отрезок ОС, равный отрезку ОА. Пусть точка D — точка пересечения отрезка АС и прямой l. Треугольник AOD равен треугольнику COD по первому признаку равенства треугольников, т. к. АО = ОС, сторона OD — общая,

2. Докажем единственность перпендикуляра.

Воспользуемся методом доказательства от противного. Предположим, что из точки А можно провести еще один перпендикуляр АD к прямой l. Пусть DС — луч, противоположный лучу DА, и DС = DА (рис. 68, б). Треугольники D₁DA и D₁DС равны по первому признаку равенства треугольников, так как DС = DА, сторона DD₁— общая, ADD₁ = CDD₁. Следовательно, AD₁D = CD₁D. Так как по предположению AD₁D = 90°, то CD₁D = 90°, т. е. угол AD₁C развернутый и лучи D₁A и D₁C составляют прямую. Таким образом, получаем, что через две точки А и С проходят две прямые, что противоречит аксиоме о существовании единственной прямой, проходящей через две точки. Значит, предположение о том, что из точки можно провести два перпендикуляра к прямой, неверно. Следовательно, такой перпендикуляр единственный.

Теорема 2. Если две прямые плоскости перпендикулярны третьей прямой этой плоскости, то они не пересекаются.

Пусть прямые а и b перпендикулярны прямой l. Докажем, что прямые а и b не пересекаются. Допустим, что прямые а и b пересекаются в некоторой точке О. Пусть прямые а и b пересекают прямую l в точках F и D соответственно. Тогда получаем, что из точки О к прямой l проведены два перпендикуляра OF и ОD. Это противоречит теореме о существовании единственного перпендикуляра, проведенного из точки к прямой. Значит, наше предположение о том, что прямые а и b пересекаются, неверно. Прямые а и b не пересекаются.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник