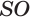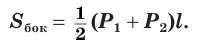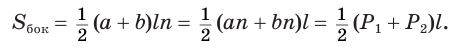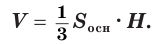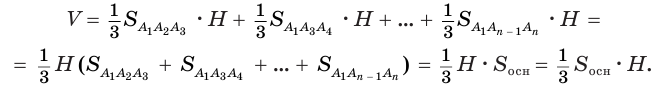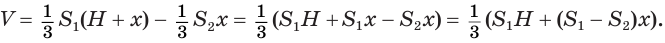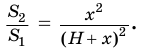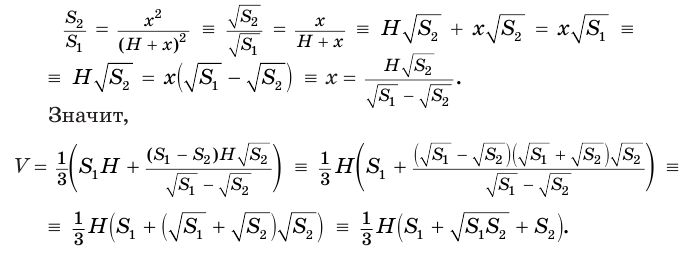Что такое основание пирамиды
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
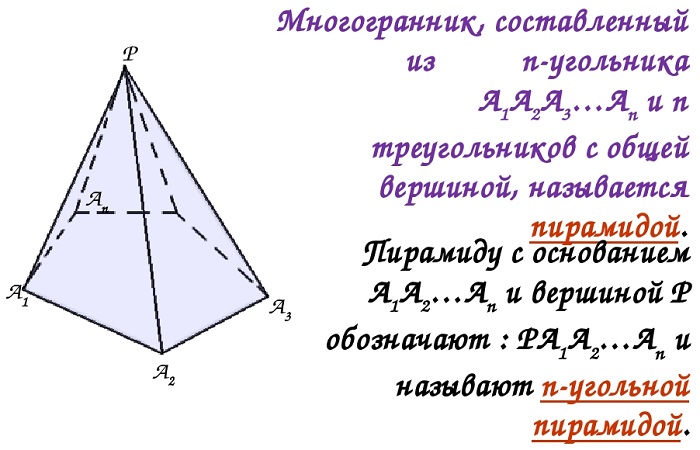
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
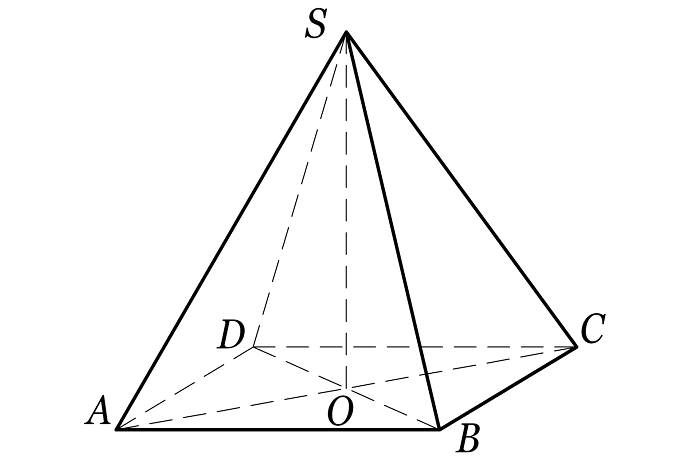
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Пирамида
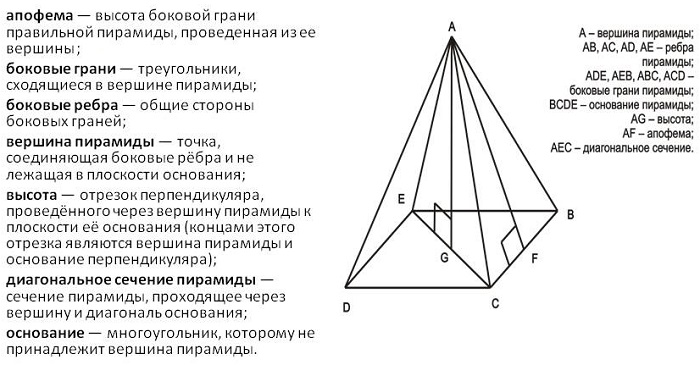
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
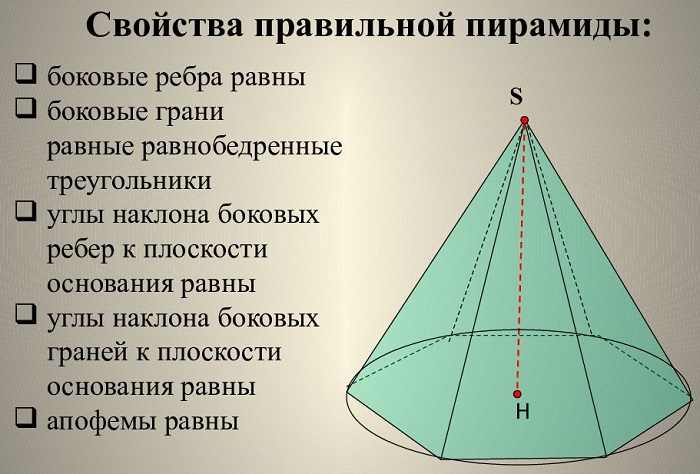
Некоторые свойства пирамиды
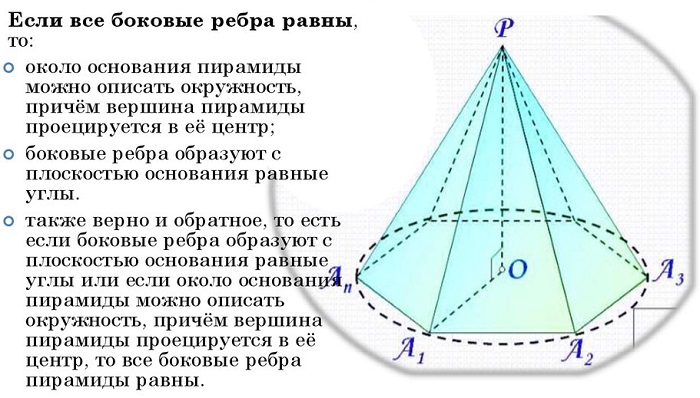
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Виды пирамид
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
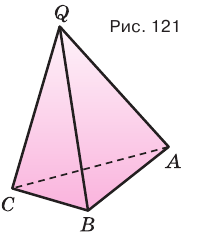
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Пирамида является одной из основных фигур в геометрии. О её особенностях рассказано в статье.
Определение пирамиды в геометрии
Эта стереометрическая фигура включает в себя часть пространства, отделённую плоскими многоугольниками: произвольным в основании и гранями — треугольниками, содержащими общую вершину и отрезок в виде общей стороны с ним.
Элементы пирамиды
Элементами этой геометрической фигуры являются:
Место, куда сходятся все боковые грани фигуры, является вершиной.
Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.
Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.
Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.
На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.
Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.
У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.
Виды пирамид
Такие фигуры могут относиться к различным видам, в зависимости от типа основания и расположения вершины.
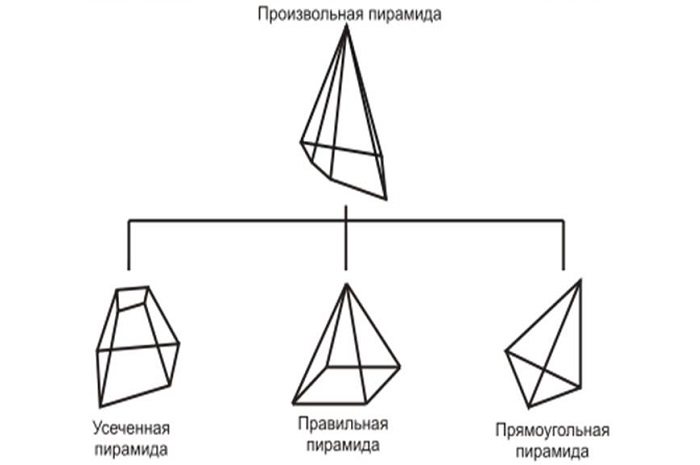
Можно указать следующие разновидности пирамид:
Правильной она будет в том случае, если в основании лежит правильный многоугольник. Проекция вершины на многоугольник основания должна приходиться на центр. Тетраэдр рассматривается как одна из разновидностей правильной пирамиды.
У прямоугольной фигуры одна из граней находится в плоскости, перпендикулярной многоугольнику, лежащему в основании.
Усеченная — это часть фигуры, находящаяся между пересекающей плоскостью и многоугольником основания. Причём эта плоскость должна располагаться горизонтально.
Свойства пирамиды
У этой объёмной геометрической фигуры имеются следующие свойства при условии равенства боковых рёбер:
круг возможно описать вокруг многоугольника основания;
угол, под которым наклонены боковые грани, будет таким же.
В том случае, когда треугольные грани имеют одни и те же углы с основанием, возможно сделать вывод о том, что их рёбра одинаковы.
Свойства правильной пирамиды
У такой фигуры можно отметить особые свойства.
У правильной пирамиды все боковые треугольники одинаковы.
Каждая из них является равнобедренным треугольником.
Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.
Снаружи возможна сфера, касающаяся всех вершин.
Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.
Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.
Формулы объема и площади поверхности пирамиды с примерами расчета
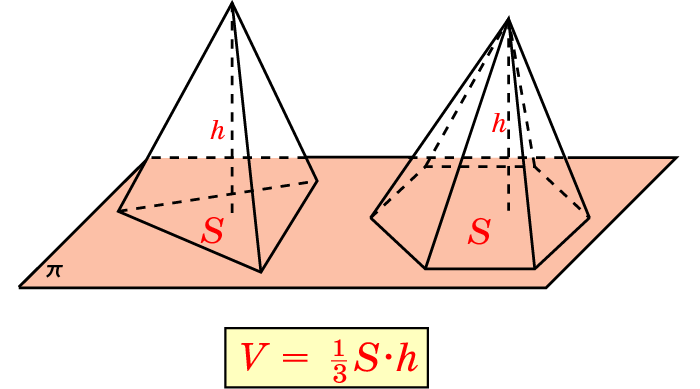
Вычислить объём можно с использованием следующей формулы.
где используются такие обозначения:
S – площадь основания;
Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.
Пример решения задачи
Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры.
Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата.
Здесь рассматривается четырехугольная пирамида.
По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.
Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.
V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.
Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см.
Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.
Пирамида
:cut Узнать, как это доказывается
Для решения задания 8 эту формулу помнить не нужно, а вот для задания 14 она может пригодиться.
Во многих задачах требуется найти площадь полной или боковой поверхности пирамиды. Боковая поверхность складывается из поверхностей боковых граней. Полная поверхность состоит из боковой поверхности и основания пирамиды.
Поскольку боковые грани пирамиды — это треугольники, то площадь боковой грани равна половине произведения основания этой грани на высоту этой грани.
Далее мы рассмотрим особый случай пирамиды — правильную пирамиду.
Правильная пирамида
Воспользуйтесь этой формулой, чтобы решить следующие две задачи:
У некоторых многогранников (не у всех) существует вписанная или описанная сфера.
Вписанная сфера — это сфера, которая касается всех граней многогранника. Описанная сфера — сфера, на которой лежат все вершины многогранника.
Проверьте свою пространственную интуицию, ответив на следующий вопрос:
Отметьте все свойства, которые обязательно должны быть выполнены в правильной пирамиде. То есть свойства, которые следуют из определения пирамиды:
Все боковые ребра пирамиды равны друг другу;
Все боковые ребра одинаково наклонены к плоскости основания;
Все ребра пирамиды равны друг другу;
Боковые грани являются равными треугольниками;
Боковые грани являются равнобедренными треугольниками;
Боковые грани одинаково наклонены к плоскости основания;
Боковые грани являются правильными треугольниками;
В правильную пирамиду можно вписать сферу;
Вокруг правильной пирамиды можно описать сферу.
:cut Узнать доказательства некоторых свойств
Остальные свойства можете попробовать доказать самостоятельно. Для того, чтобы доказать, что боковые грани одинаково наклоненые к плоскости основания и что ребра одинаково наклонены к плоскости основания, нужно знать, что такое угол между плоскостями и угол между прямой и плоскостью. Об этом рассказывается в уроке Основные теоремы стереометрии
Правильный тетраэдр — это треугольная пирамида, у которой все ребра равны.
Площадь поверхности, объем, высоту и другие элементы правильного тетраэдра можно найти, если знать, чему равно ребро правильного тетраэдра. Зная только лишь длину одного ребра правильного тетраэдра, мы знаем о нем все.
Для правильного тетраэдра выполняются следующие свойства:
Заучивать все формулы без разбора — это довольно бесполезное занятие. Формулы, записанные выше, используются не так часто, и при этом их можно легко вывести из основных формул.
Например, площадь поверхности правильного тетраэдра можно найти, если умножить площадь равностороннего треугольника со стороной a a a на число граней тетраэдра: 4 ⋅ 3 4 a 2 4\cdot \frac<\sqrt<3>> <4>a^2 4 ⋅ 4 3
В стереометрии важно понимать, как связаны друг с другом различные элементы тел, и помнить основные формулы планиметрии, такие как формула площади треугольника и параллелограмма. Выучите самые основные формулы стереометрии, такие как формула объема пирамиды и призмы, и научитесь выводить все остальные формулы.
Очень часто ключом к решению является первый шаг, который позволит свести задачу по стереометрии к планиметрии.
Рассмотреть сечение, проходящее через высоту и боковое ребро пирамиды
Выразить высоту, используя формулу площади грани
Применить теорему Пифагора к треугольнику в основании пирамиды
:cut Узнать, как вывести остальные формулы
Задачи для самостоятельного решения: #пирамида
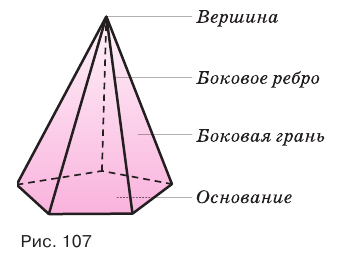
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
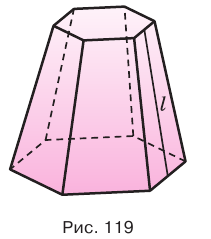
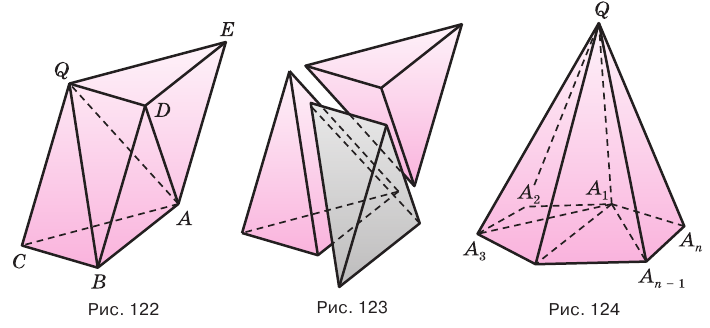
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
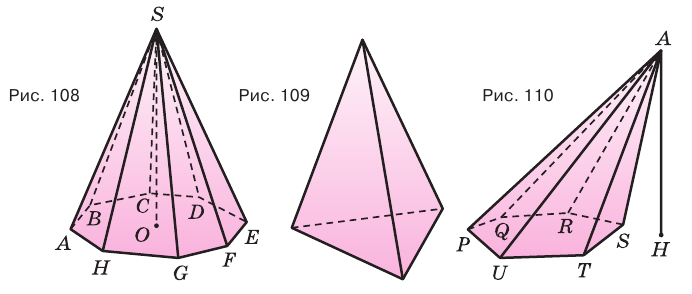
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
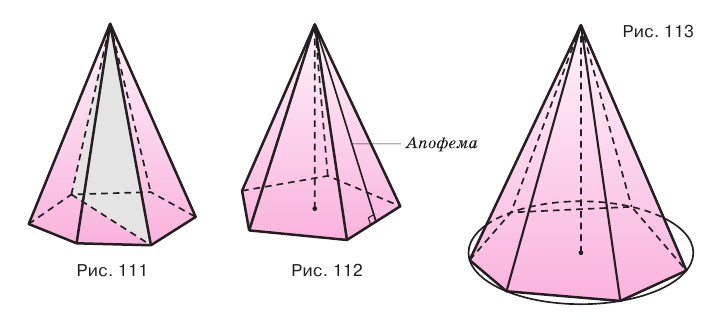
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
Отметим, что если в пирамиде равны все:
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
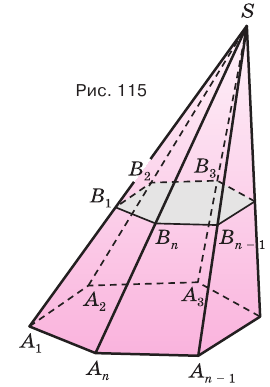
Используя рисунок 115, докажите эту теорему самостоятельно.
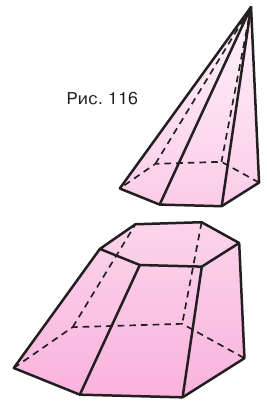
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
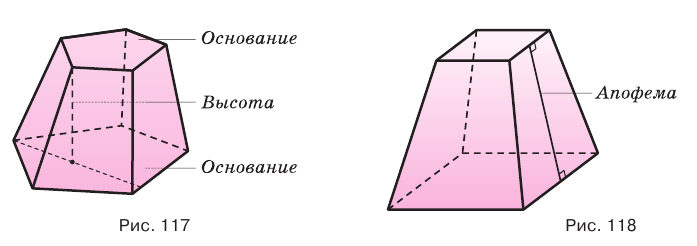
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 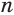
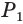
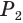
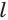
Боковая поверхность данной пирамиды состоит из 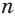
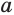
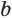
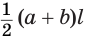
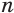
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
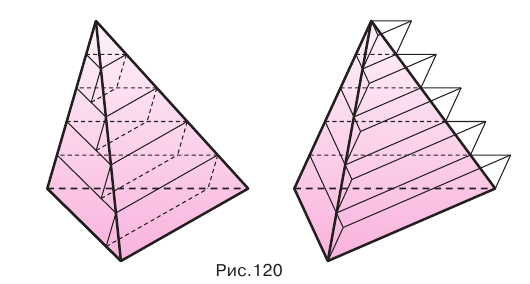
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 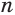
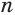
Пусть 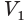
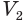


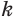
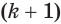


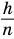
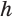
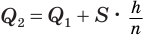
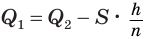
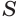
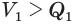
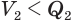
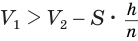
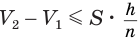
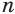
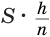
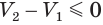
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 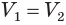
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

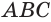
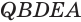
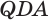


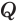
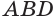
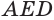




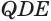

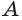
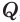





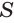

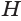



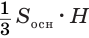
Пусть теперь есть произвольная пирамида 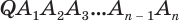
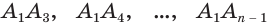
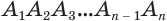
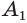
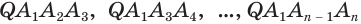

Пример:
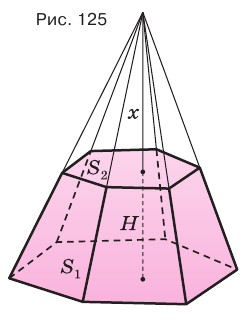
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 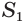
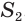

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 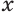
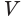
Чтобы найти высоту 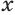
Решим это уравнение, учитывая, что 

Таким образом, объем 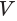
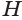


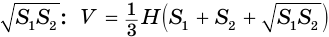
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.