Что такое основная и дополнительная погрешности приборов
Погрешность измерений
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
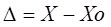
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
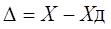
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
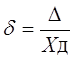
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
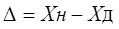
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
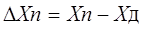
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
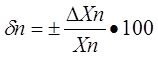
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
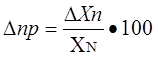
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
Основная и дополнительная погрешности.
Погрешности СИ зависят от внешних условий (условия окружающей среды), поэтому различаются основные и дополнительные погрешности.
Основные погрешности – это погрешности, которые возникают при условиях окружающей среды, принятых за нормальные условия (НУ).
Дополнительные погрешности – это погрешности, возникающие при отклонении условий окружающей среды от НУ.
С учетом влияния условий окружающей среды на СИ можно записать статическую характеристику преобразования в виде
Y=F(X, ξ1, ξ2, ξ3, …, ξn), (1)
где ξ1 – ξn – это влияющие величины (факторы)
X и Y – это входная и выходная и выходная величины соответственно
Как следует из формулы (1) изменение выходной величины ΔY зависит от
Следовательно, в общем, виде изменения входной величины можно запи-
сать следующим образом:
В формуле (2) второе и последующее слагаемые являются слагаемыми в по-
грешности влияющих величин. Если изменение влияющих величин находит-
ся в пределах НУ, то все составляющие в формуле (2) входят в состав основ-
ной погрешности. Если изменение влияющих величин больше чем преду-
смотрено нормальными условиями, то приращение ΔY включает также до-


 |




 |

Рисунок 3. Вариации выходного сигнала
По зависимости погрешности СИ от измеряемой величины разделяют два
Аддитивная погрешность – это погрешность, абсолютное значение которой не зависит от измеряемой величины.
 |
|














 |
Рисунок 4. Аддитивная погрешность
где Δy – абсолютная аддитивная погрешность
Мультипликативная погрешность – это погрешность, абсолютное значение которой пропорционально входной величине.
Мультипликативную погрешность иногда называют погрешностью чувствительности.








Рисунок 5. Мультипликативная погрешность
Отличие этих сигналов состоит в том, что S*= K·S
Основная и дополнительная погрешности
Основная инструментальная погрешность находится по классу точности СИ. Например, при нормальных условиях щитовым электромагнитным вольтметром класса точности 1,5 (т.е. имеющим предел основной приведенной погрешности γn не превышающий ±1,5 %) с диапазоном измеряемых значений 0. 300 В (нормирующее значение Хн = 300 В) получен результат измерения действующего значения напряжения U= 220 В. Требуется определить предельные значения абсолютной Δ и относительной δ инструментальных погрешностей результата измерения U.
Оценим предельное значение основной абсолютной погрешности Δ:

Предельное значение основной относительной погрешности δ:
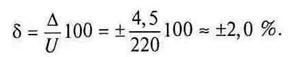
Расчет суммарной погрешности результата измерения в общем случае предполагает нахождение максимально возможного числа составляющих (основной, дополнительной, методической, взаимодействия и т.д.).
Дополнительная погрешность возникает при работе СИ (в частности, прибора) не в нормальных, а в рабочих условиях, когда одна или несколько влияющих величин выходят за пределы области нормальных значений (но находятся внутри диапазона рабочих значений).
Влияющая величина (ВВ) — это такая физическая величина β, которая не измеряется в данном эксперименте, но влияет на результат измерения или преобразования. Например, в эксперименте по измерению тока в электрической цепи некоторые другие физические величины (температура окружающей среды, атмосферное давление, относительная влажность воздуха, электрические и магнитные поля, напряжение питания СИ) являются влияющими величинами. Однако, если мы измеряем температуру окружающей среды, то в данном эксперименте температура есть измеряемая величина.
Влияющие величины в общем случае могут меняться в довольно широких диапазонах. При оценке работоспособности СИ в различных условиях воздействия окружающей среды различают три области возможных значений ВВ:
• область нормальных значений ВВ когда значение ВВ находится в пределах заранее оговоренных (нормальных) значений;
• область рабочих значений ВВ когда значение ВВ находится в диапазоне своих рабочих значений;
• область значений ВВ, при которых возможны хранение или транспортировка СИ.
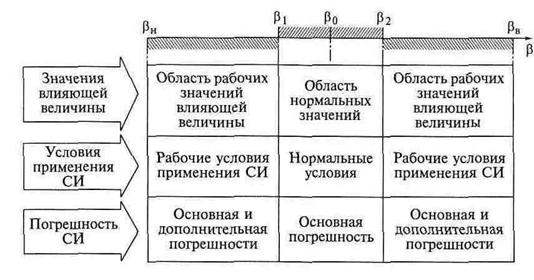
С точки зрения оценки инструментальных погрешностей нас интересуют лишь первые две области (рис. 2.5).
Область нормальных значений ВВ обычно задается симметричным относительно номинального значения β0 диапазоном β1….β0 В этом диапазоне возможных значений ВВ условия применения СИ считаются нормальными (НУ) и при этом имеет место только основная погрешность СИ.
Рис. 2.5. Значения влияющей величины, условия применения и погрешности средств измерений
Областью рабочих значений называется более широкий диапазон возможных изменений ВВ, в котором СИ может нормально использоваться. Границы этого диапазона задаются нижним βн и верхним βв предельными значениями ВВ, соответственно. В этом диапазоне значений ВВ условия применения СИ называются рабочими (РУ) и при этом имеет место не только основная, но еще и дополнительная погрешность. Таким образом, при работе в пределах рабочих условий, но за пределами нормальных, общая инструментальная погрешность складывается уже из основной и дополнительной составляющих.
Например, для самой важной практически во всех измерительных экспериментах ВВ — температуры окружающей среды — область нормальных (для России) значений и, следовательно, нормальных условий применения СИ в большинстве обычных технических измерительных экспериментов составляет (20 ± 5) °С или (20 ± 2) °С.
Области нормальных значений не являются постоянными, а зависят от особенностей выполняемых измерений, измеряемых величин, классов точности СИ. Например, чем точнее СИ, тем уже требуемый диапазон нормальных температур. Для мер электрического сопротивления высшего класса точности (0,0005; 0,001; 0,002) допустимое отклонение температуры от номинального значения составляет, соответственно, ±0,1°С; ±0,2°С; ±0,5°С. Для зарубежных приборов часто за номинальное принимается значение температуры +23°С. Номинальные значения и диапазоны нормальных значений некоторых основных ВВ для обычных измерений приведены в табл. 2.3.
Области нормальных значений ВВ в специальных измерениях оговариваются отдельно в описании СИ или в методиках проведения измерений.
Таблица 2.3. Диапазоны нормальных значений влияющих величин
| Влияющая величина | Значение |
| Температура окружающей среды, °С | 20±5 или20±2 |
| Относительная влажность воздуха, % | 55. 60 |
| Атмосферное давление, кПа (мм рт. ст.) | 100 ±4 (750 ±30) |
| Действующее значение напряжения питающей сети, В | 220±10% |
| Частота напряжения питающей сети, Гц | 50±1% |
| Максимальный коэффициент нелинейных искажений напряжения питающей сети, % | 5 |
Диапазоны рабочих условий эксплуатации для СИ разного назначения различны. Скажем, для СИ лабораторного применения это может быть диапазон температур О. +40 °С (рис. 2.6).
Для СИ промышленного применения области рабочих значений ВВ являются более широкими, чем, скажем, для лабораторных СИ. Измерительная аппаратура военного назначения имеет еще более широкие области рабочих значений ВВ.
Зная класс точности, коэффициенты влияния окружающей среды (например, температурный коэффициент), а также коэффициенты влияния неинформативных параметров измеряемых сигналов (например, частоты периодического сигнала напряжения при измерении действующего значения), можно оценить значение дополнительной погрешности и затем найти суммарную инструментальную, сложив основную и дополнительную составляющие.
Рис. 2.6. Диапазоны возможных значений влияющей величины — температуры окружающей среды
Рассмотрим пример нахождения оценки дополнительной составляющей инструментальной погрешности на примере влияния только одной (но самой важной и, к счастью, наиболее легко определяемой) ВВ — температуры. Допустим, после выполнения эксперимента по классу точности миллиамперметра найдена его основная инструментальная погрешность Δ0 = ±1,0 мА; температура в ходе эксперимента была зафиксирована +28 °С. Температурный коэффициент в паспорте на прибор определен таким образом: «. дополнительная погрешность на каждые 10°С отличия от номинальной температуры +20 °С равна основной погрешности в пределах изменения температуры окружающей среды от 0 до +50 °С». Тогда предельное значение дополнительной абсолютной погрешности Δд в данном случае определяется следующим образом:
Методическая погрешность
Как известно, погрешность результата измерения определяется не только классом точности СИ. Источниками недостоверности результата могут быть и другие причины. Рассмотрим примеры, поясняющие появление методической составляющей общей погрешности результата.
Представим эксперимент по косвенному измерению мощности на активной нагрузке R методом амперметра и вольтметра (рис. 2.7). В результате простого перемножения показаний вольтметра UV и амперметра IA мы получаем не совсем то значение, которое следовало бы, поскольку в этом эксперименте возникает погрешность, определяемая не классами точности приборов, а другими их характеристиками (например, внутренними сопротивлениями) и методом их использования (например, схемой включения).
Вольтметр в этой схеме реагирует на сумму (UR + UA), т.е. на сумму падений напряжений на нагрузке R и на внутреннем сопротивлении амперметра RA. Показания вольтметра UV, вычисленное Р и действительное Рд значения мощности, соответственно, равны:
PД = I 2 R (2.10)
Таким образом, в данном случае причина ошибки в наличии конечного (хоть и малого, но не нулевого) внутреннего сопротивления амперметра RA .
Рис. 2.7. Возникновение методической погрешности при различном подключении приборов:
а — вольтметр—амперметр; б — амперметр—вольтметр
Значение методической погрешности результата измерения мощности в абсолютном Δ и относительном δ видах в данном случае можно оценить следующим образом:
δ = 100Δ/PД = 100RA/R (2.12)
Зная значение сопротивления амперметра RA, можно, во-первых, оценить значение методической погрешности для данного случая, а во-вторых, можно скорректировать (исправить) результат вычисления мощности.
Рассмотрим количественный пример. Пусть в схеме рис. 2.7a, использован амперметр с внутренним сопротивлением RA = 10 Ом. Получены показания вольтметра и амперметра: UV = 250 В, IА = 2 А. Вычисленная по этим показаниям мощность Р = = 500 Вт. Абсолютная методическая погрешность Δ = I 2 ARA = 4•10 = 40 Вт, что составляет 8 % результата измерения. Правда, в данном случае, при точном знании сопротивления RA, знак и значение этой погрешности известны точно. Таким образом, эту составляющую в этом примере можно практически полностью скомпенсировать (простым уменьшением вычисленного результата Р на значение Δ = 40 Вт).
Отметим, что изменение схемы включения приборов (перенос амперметра ближе к источнику ЭДС Е, рис. 2.7б) не исключает методическую погрешность, а просто несколько меняет ее природу. В этом случае причиной погрешности будет конечное внутреннее сопротивление RV вольтметра, текущий через него ток IV, а значит несколько завышенное показание амперметра IA= IR+ IV.
Чем меньше отношение значений сопротивления амперметра ra и нагрузки R в схеме рис. 1.13, а, тем лучше, т.е. тем меньше погрешность.
Для второй схемы (см. рис. 2.7б), чем выше сопротивление вольтметра RV по сравнению с сопротивлением нагрузки R, тем лучше.
Можно было бы по отдельности измерять напряжение и ток, поочередно включая вольтметр и амперметр. Но при такой организации эксперимента необходимо иметь уверенность, что измеряемые величины не изменяются в процессе эксперимента. Иначе может появиться значительная динамическая погрешность.
Погрешность взаимодействия
Эта составляющая общей погрешности результата возникает из-за конечных сопротивлений источника сигнала и прибора. На рис. 2.8 показан вольтметр, входное сопротивление которого хоть и велико, но не бесконечно.
Рис. 2.8. Погрешность взаимодействия вольтметра и источника напряжения
При подключении вольтметра к источнику ЭДС в цепи потечет ток I, определяемый значением ЭДС ЕX а также значениями внутреннего сопротивления источника Rи и входного сопротивления прибора RV. Поэтому измеряемое вольтметром напряжение всегда будет несколько меньше значения ЭДС ЕX, что и приводит к появлению погрешности взаимодействия ΔВЗ. Погрешность взаимодействия ΔВЗ вольтметра и источника напряжения определяется следующим образом:
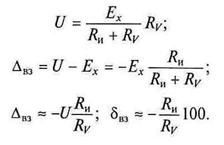
Оценим значение погрешности взаимодействия на примере. Предположим, к источнику ЭДС ЕХ = 10 В, имеющему внутреннее сопротивление RИ = 10 Ом, подключен аналоговый вольтметр с внутренним сопротивлением RV = 10 кОм. Пренебрегая всеми остальными погрешностями, определим показание прибора, значения абсолютной и относительной погрешностей взаимодействия. В данном случае показание вольтметра
UV = 10В•10кOм/(10кОм + 0,01кОм) = 9,99 В. Абсолютное и относительное значения погрешности взаимодействия равны соответственно:
При измерениях тока амперметрами также возникает погрешность взаимодействия (рис.2.9).
Рис. 2.9. Влияние амперметра на ток в цепи
Амперметр имеет малое, но не нулевое внутреннее сопротивление RA, и при включении его в цепь ток в ней несколько уменьшается.
Если пренебречь малым значением внутреннего сопротивления RИ источника Е, считая, что оно гораздо меньше сопротивления нагрузки RН (RИ
Дата добавления: 2018-06-27 ; просмотров: 4757 ; Мы поможем в написании вашей работы!