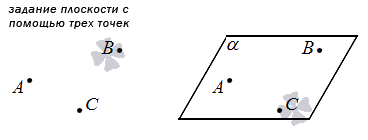Что такое основная плоскость
Основная плоскость
Основна́я плоскость — в теории корабля горизонтальная плоскость, проходящая через самую нижнюю точку корпуса корабля (судна) (не считая выступающих частей). Входит в число основных точек, линий и плоскостей теоретического чертежа.
Пересечением основной плоскости с диаметральной образуется основная линия — продольная ось X в системе координат, привязанной к судну. В основной плоскости также лежит поперечная ось Y, образуемая пересечением с плоскостью мидель-шпангоута.
См. также
Полезное
Смотреть что такое «Основная плоскость» в других словарях:
основная плоскость — (Pv) Координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания в этой точке. Примечание В инструментальной системе координат направление… … Справочник технического переводчика
основная плоскость — 2.4 основная плоскость (base plan): Горизонтальная плоскость, проходящая через линию пересечения киля с наружной поверхностью обшивки в середине длины шлюпки. Источник: ГОСТ Р ИСО 4143 2005: Судостроение. Суда внутреннего плавания. Шлюпки… … Словарь-справочник терминов нормативно-технической документации
основная плоскость конуса — основная плоскость Плоскость, перпендикулярная к оси конуса, в которой задается номинальный диаметр конуса. Наружный конус Внутренний конус 1 основная плоскость; 2 базовая плоскость. [ГОСТ 25548 82 (CT СЭВ 1779 79)] Тематики нормы… … Справочник технического переводчика
основная плоскость конической резьбы — основная плоскость Плоскость, перпендикулярная к оси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие… … Справочник технического переводчика
основная плоскость судна — (ОП) Горизонтальная плоскость, проходящая через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель шпангоута. [ГОСТ 1062 80] Тематики корабли и суда Обобщающие термины плоскости и линии для установления главных размерений… … Справочник технического переводчика
основная плоскость конической резьбы — 3.1.30 основная плоскость конической резьбы: Плоскость, перпендикулярная коси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы. Источник … Словарь-справочник терминов нормативно-технической документации
Основная плоскость плавучего дока — 6. Основная плоскость плавучего дока ОП Горизонтальная плоскость, проходящая через нижнюю точку теоретической поверхности корпуса плавучего дока без учета выступающих частей Источник: ГОСТ 14181 78: Доки плавучие. Термины, определения и буквенные … Словарь-справочник терминов нормативно-технической документации
Основная плоскость судна — 15. Основная плоскость судна По ГОСТ 1062 80 Источник: ГОСТ 13641 80: Элементы мет … Словарь-справочник терминов нормативно-технической документации
основная плоскость пучка скоростей звена — Плоскость, на которой лежат концы векторов абсолютных скоростей, составляющих пучок скоростей звена … Политехнический терминологический толковый словарь
инструментальная основная плоскость — (Pvи) Основная плоскость инструментальной системы координат. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости EN tool reference plane DE Werkzeug Bezugsebene FR … Справочник технического переводчика
основная плоскость
2.4 основная плоскость (base plan): Горизонтальная плоскость, проходящая через линию пересечения киля с наружной поверхностью обшивки в середине длины шлюпки.
3.2.10 основная плоскость: Плоскость, проходящая через точку на режущей кромке перпендикулярно к верхней стороне полотна (см. рисунки 1 и 5).
3.3 Разводка зубьев и общая разводка
Смотри также родственные термины:
3.1.30 основная плоскость конической резьбы: Плоскость, перпендикулярная коси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы.
ДОПОЛНИТЕЛЬНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ КОНИЧЕСКОЙ РЕЗЬБЫ
Плоскость, перпендикулярная к оси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы (черт. 32)
6. Основная плоскость плавучего дока
Горизонтальная плоскость, проходящая через нижнюю точку теоретической поверхности корпуса плавучего дока без учета выступающих частей
15. Основная плоскость судна
Полезное
Смотреть что такое «основная плоскость» в других словарях:
Основная плоскость — (обозначена Baseline). От нее отсчитываются все вертикальные размеры Основная плоскость в теории корабля горизонтальная плоскость, проходящая через самую нижнюю точку корпуса корабля (судна) (не считая выступающих частей). Входит в число… … Википедия
основная плоскость — (Pv) Координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания в этой точке. Примечание В инструментальной системе координат направление… … Справочник технического переводчика
основная плоскость конуса — основная плоскость Плоскость, перпендикулярная к оси конуса, в которой задается номинальный диаметр конуса. Наружный конус Внутренний конус 1 основная плоскость; 2 базовая плоскость. [ГОСТ 25548 82 (CT СЭВ 1779 79)] Тематики нормы… … Справочник технического переводчика
основная плоскость конической резьбы — основная плоскость Плоскость, перпендикулярная к оси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие… … Справочник технического переводчика
основная плоскость судна — (ОП) Горизонтальная плоскость, проходящая через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель шпангоута. [ГОСТ 1062 80] Тематики корабли и суда Обобщающие термины плоскости и линии для установления главных размерений… … Справочник технического переводчика
основная плоскость конической резьбы — 3.1.30 основная плоскость конической резьбы: Плоскость, перпендикулярная коси резьбы, в которой задаются номинальные размеры наружного, среднего и внутреннего диаметров конической резьбы. Источник … Словарь-справочник терминов нормативно-технической документации
Основная плоскость плавучего дока — 6. Основная плоскость плавучего дока ОП Горизонтальная плоскость, проходящая через нижнюю точку теоретической поверхности корпуса плавучего дока без учета выступающих частей Источник: ГОСТ 14181 78: Доки плавучие. Термины, определения и буквенные … Словарь-справочник терминов нормативно-технической документации
Основная плоскость судна — 15. Основная плоскость судна По ГОСТ 1062 80 Источник: ГОСТ 13641 80: Элементы мет … Словарь-справочник терминов нормативно-технической документации
основная плоскость пучка скоростей звена — Плоскость, на которой лежат концы векторов абсолютных скоростей, составляющих пучок скоростей звена … Политехнический терминологический толковый словарь
инструментальная основная плоскость — (Pvи) Основная плоскость инструментальной системы координат. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости EN tool reference plane DE Werkzeug Bezugsebene FR … Справочник технического переводчика
Что такое основная плоскость
ОСНОВЫ ТЕОРИИ РЕЗАНИЯ МАТЕРИАЛОВ
Лекция 1.2.
Элементы конструкции и геометрические параметры режущей части
инструмента (на примере токарного резца)
Геометрия токарного резца ( Продолжительность видео 10 минут )
Понятие о процессе резания (Продолжительность видео 30 минут)
Токарные резцы (Продолжительность видео 34 минуты)
Текст для чтения вслух (Microsoft Edge) и с мобильных устройств
Любой режущий инструмент нужно рассматривать с двух точек зрения: как некоторое геометрическое тело определенной формы и размеров или как орудие труда, с помощью которого осуществляется определенный вид обработки. В соответствии с этим и геометрические параметры инструмента целесообразно разделять на параметры инструмента как геометрического тела, необходимые при изготовлении инструмента (так называемые инструментальные углы или углы заточки), и параметры инструмента в процессе резания, которые определяют условия протекания процесса (так называемые рабочие углы или кинематические). Придав инструменту в ходе его работы те или иные движения или изменив соотношение скоростей этих движений, можно при неизменных углах заточки получить различные по величине кинематические углы.
Инструментальная система координат (ИСК) применяется при изготовлении и контроле инструментов. Именно углы, определенные в ИСК, указываются на рабочих чертежах инструментов.
Статическая система координат (ССК) является чаще всего используемой на практике. Применяется для приближенного определения углов лезвия в процессе резания и для учета изменения этих углов при установке инструмента на станке.
Кинематическая система координат (КСК). Применяется для определения действительных (рабочих) углов лезвия, которые имеют место непосредственно в процессе резания.
Координатные плоскости любой системы координат взаимно перпендикулярны, а центр их пересечения лежит в рассматриваемой точке А на режущей кромке. На рис. 1.14 показано расположение координатных плоскостей для процесса продольного точения (обтачивания). Для всех других видов обработки резанием определение их расположения проводится по нижеуказанным правилам:
· P v – основная плоскость ( 1 ) – это координатная плоскость, проведенная через заданную точку А режущей кромки, перпендикулярно направлению скорости главного V (ССК) или результирующего V e (КСК) движения резания в этой точке;
· P n – плоскость резания ( 2 ) – это координатная плоскость, касательная к режущей кромке в точке А и перпендикулярная к основной плоскости;
· P τ – главная секущая плоскость ( 3 ) – это координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания в точке А ;
· φ – главный угол в плане – это угол между плоскостью резания P n и рабочей плоскостью P S ;
· φ 1 – вспомогательный угол в плане – это угол между рабочей плоскостью P S и проекцией вспомогательной режущей кромки на основную плоскость P v ;
· γ – главный передний угол – это угол между передней поверхностью лезвия и основной плоскостью;
· α – главный задний угол – это угол между главной задней поверхностью лезвия и плоскостью резания P n ;
· β – главный угол заострения – это угол между передней и задней поверхностями лезвия;
В обозначениях координатных плоскостей и параметров лезвия применяются индексы, которые отвечают системе: «и» – в ИСК; «с» – в ССК; «к» – в КСК. Например, P v с – основная плоскость ССК, P v к – основная плоскость КСК. γ с – передний угол в ССК, γ к – передний угол в КСК, γ и – передний угол в ИСК.
Инструментальные геометрические параметры лезвия резца в ИСК представлены на рис. 1.15, рис 1.16, рис 1.17.
При заточке резцов на некоторых моделях заточных станков необходимо знать величину передних и задних углов в сечениях плоскостями P–P и P 1 –P 1 (рис. 1.18).
Плоскость P–P расположена перпендикулярно к основной и параллельно боковой плоскостям. Ее называют продольной секущей плоскостью. Плоскость P 1 –P 1 еще называют поперечной секущей плоскостью. Углы резца, расположенные в отмеченных плоскостях, соответственно, называют продольными и поперечными.
В соответствии с определением базой для ориентации статической системы координат является направление вектора скорости главного движения резания. Как правило, режущие инструменты устанавливаются таким образом, чтобы осевая плоскость заготовки, которая проходит через рассматриваемую точку режущей кромки (вершину) лезвия инструмента, была параллельной опорной плоскости 1 резца (см. рис. 1.15). В этом случае вектор скорости главного движения перпендикулярен и к опорной плоскости, и к основной, а, значит, ИСК и ССК совпадают между собой, как и инструментальные, и статические углы режущей части.
Результатом этого будет отличие между значениями инструментальных и статических углов в плане j и φ 1 :
В современных условиях задача определения статических углов режущей части приобрела особенную актуальность с применением инструментов, оснащенных сменными неперетачиваемыми пластинами (СНП). Как правило, такие пластины представляют собой сформированную режущую часть инструмента и в своем большинстве не имеют инструментального заднего угла. Углы α с и α 1с у них обеспечиваются установкой пластины под соответствующими углами по отношению к осевой плоскости детали. Вследствие этого статические углы режущего инструмента γ с и λ с определяются как формой режущего лезвия самой пластины, так и ее установкой относительно заготовки. Для их расчета рационально использовать метод ортогонального проектирования.
Основным условием при такой обработке является недопущение нулевого значения углов φ к или φ 1к поскольку это приведет к подрезанию профиля детали.
Плоская передняя поверхность резца, изображенная на рис. 1.15, во многих случаях резания не является оптимальной. Если режущая часть инструмента изготовлена из быстрорежущей стали или твердого сплава, то в зависимости от вида обрабатываемого материала
и условий работы рекомендуют три формы передней поверхности (рис. 1.23): криволинейная с фаской; плоская с фаской; плоская с положительным или отрицательным передним углом.
Для каждой из указанных форм передней поверхности существуют рекомендованные области их эффективного применения.
Величина заднего угла a мало зависит от механических свойств материала обрабатываемой заготовки и определяется величиной подачи S или максимальной толщиной срезаемого слоя.
Величина главного (j) и вспомогательного (φ 1 ) углов в плане зависит от назначения резца и жесткости технологической системы резания. Обычно j = 30…90°, а φ 1 = 5…30°.
При λ ≠ 0 меняется положение передней поверхности относительно направления скорости резания и направления схода стружки (рис. 1.24). Когда λ = 0, стружка сходит перпендикулярно режущей кромке. Если же λ ≠ 0, то стружка кроме указанного движения V с получает движение вдоль режущей кромки V с1 от высших ее точек к более низким: к вершине (при λ > 0) или от вершины (при λ 0 (вершина инструмента – самая низкая точка режущей кромки) стружка отклоняется в сторону обработанной поверхности (задней бабки токарного станка). Она меньше поддается запутыванию и поэтому считается более безопасной. Следовательно, инструмент с λ > 0 рекомендуется при черновой обработке, когда стружка толстая и хуже ломается.
Угол наклона главной режущей кромки l определяет место расположения точки А на режущей кромке, где происходит первый контакт (удар) со срезаемым слоем (припуском) (см. рис. 1.17). При λ всегда положительный (l = 0…5°). При прерывистом резании, независимо от вида инструментального материала, резцы имеют положительный угол наклона главной режущей кромки, величина которого лежит в пределах l = 10…30°.
При непрерывном резании резцами из быстрорежущей стали при черновой обработке рекомендуется l = 0…4°, а при чистовой обработке l = 0…–4°.
В чем измерятся судно и какие его основные плоскости?
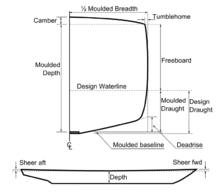
Одно судно от другого отличается геометрическими характеристиками (рис. 5). Эти характеристики своего судна, или, как их называют, главные размерения, судоводитель должен знать. Главными размерениями судна являются: длина, ширина, осадка и высота борта. Отношения между главными размерениями характеризуют форму и мореходные качества судна.
Длина габаритная — расстояние, измеренное в горизонтальной плоскости между крайними внешними кромками выступающих частей носа и кормы судна.
Ширина габаритная — расстояние, измеренное перпендикулярно диаметральной плоскости между внешними кромками выступающих частей судна в самой широкой части (привального бруса, ограждения двигателей, обносов и др.).
Осадка габаритная или наибольшая — вертикальное расстояние, измеренное в плоскости мидель-шпангоута от уровня спокойной воды, соответствующего действующей ватерлинии, до низшей точки наружной обшивки или брускового киля, а также до низшей кромки гребного винта; замеряется на стоянке и обычно отличается от осадки на ходу. То же расстояние, замеренное при тех же условиях, но без груза и пассажиров, называется осадкой порожнем.
Высота борта — вертикальное расстояние, измеренное на середине судна (миделе) от основной линии до палубы (или до планширя).
Высота надводного борта — разность между высотой борта и осадкой (Н — Т) — является величиной переменной. Для обеспечения безопасности плавания — сохранения судном плавучести, остойчивости и непотопляемости — нормируется минимальная высота надводного борта.
За базовые или основные плоскости принимают три взаимно перпендикулярные плоскости:
Диаметральная плоскость (ДП) — вертикальная продольная плоскость симметрии, которая проходит по середине ширины судна и делит судно на правую и левую части. Изображение судна в этой плоскости называется боком.
Основная плоскость (ОП) — горизонтальная плоскость, касательная к линии киля (самой кромки обшивки на деревянном судне) в его нижней точке; линия (прямая) пересечения основной плоскости с ДП называется основной линией (ОЛ). Изображение судна в этой плоскости называется полуширотой.
Плоскость мидель-шпангоута (миделя) — вертикальная поперечная плоскость, которая проходит по середине расчетной длины судна, обычно через наиболее полное поперечное сечение. Изображение судна в этой плоскости называется корпусом.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
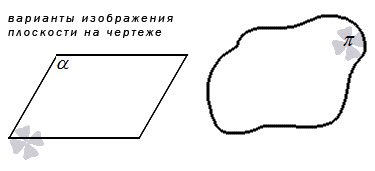
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
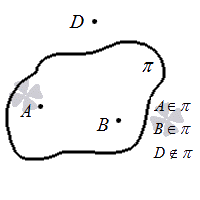
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
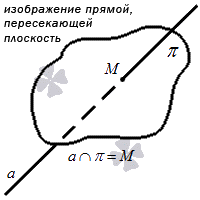
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
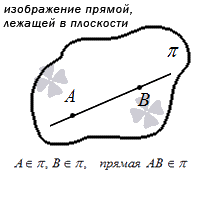
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
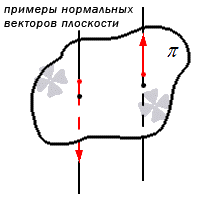
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
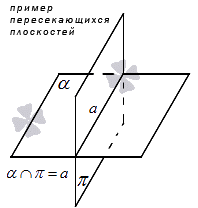
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
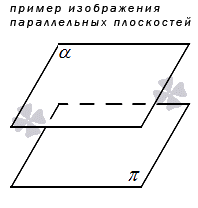
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
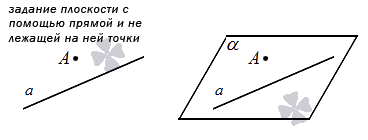
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
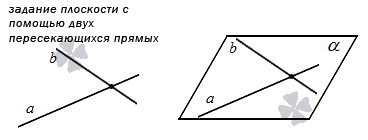
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
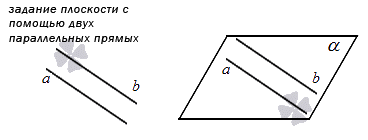
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
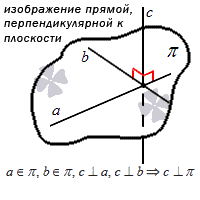
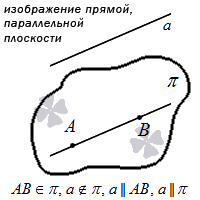
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
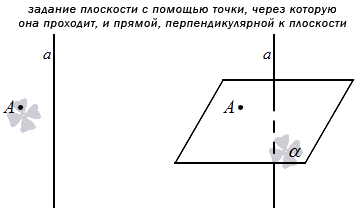
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
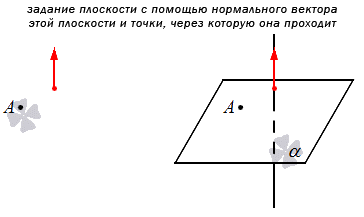
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.