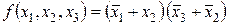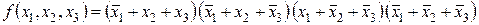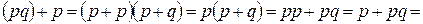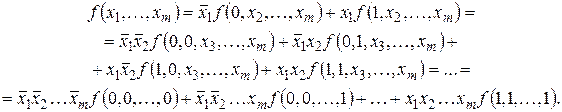Что такое основной базис алгебры логики
Булева алгебра (алгебра логики)
Понятие алгебры логики
На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».
Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.
Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Пусть функция 

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).
На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.
Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.
Логические функции
Логические функции одной переменной
| Функция | Название | Обозначение |
 | Константа нуля |  |
 | Повторение x |  |
 | Логическое отрицание, инверсия, «НЕ» |  |
 | Константа единицы |  |
| Переменная | Логические функции | |||
| x |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Логические функции двух переменных
| Функция | Название | Обозначение |
 | Константа нуля |  или False или False |
 | Логическое умножение, конъюнкция, «И» |  или или  или или  или или  |
 | Запрет по  |  или или  |
 | Переменная  |  |
 | Запрет по  |  или или  |
 | Переменная  |  |
 | Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ» |  или или  или или  |
 | Логическое сложение, дизъюнкция, «ИЛИ» |  или или  или или  или или  |
 | Функция Пирса (Вебба), «ИЛИ-НЕ» |  или или  или или  |
 | Логическая равнозначность, эквиваленция |  или или  или или  или или  |
 | Отрицание  |  |
 | Правая импликация |  или или  |
 | Отрицание  |  |
 | Левая импликация |  или или  |
 | Функция Шеффера, «И-НЕ» |  или или  или или  |
 | Константа единицы |  или True или True |
Ниже дана таблица истинности для логических функций от двух переменных.
| X1 | 0 | 0 | 1 | 1 |
| X2 | 0 | 1 | 0 | 1 |
 | 0 | 0 | 0 | 0 |
 | 0 | 0 | 0 | 1 |
 | 0 | 0 | 1 | 0 |
 | 0 | 0 | 1 | 1 |
 | 0 | 1 | 0 | 0 |
 | 0 | 1 | 0 | 1 |
 | 0 | 1 | 1 | 0 |
 | 0 | 1 | 1 | 1 |
 | 1 | 0 | 0 | 0 |
 | 1 | 0 | 0 | 1 |
 | 1 | 0 | 1 | 0 |
 | 1 | 0 | 1 | 1 |
 | 1 | 1 | 0 | 0 |
 | 1 | 1 | 0 | 1 |
 | 1 | 1 | 1 | 0 |
 | 1 | 1 | 1 | 1 |
Ответить на контрольные вопросы, а затем посмотреть ответы
Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):
Булев базис (логический базис)
Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
Инверсия (логическое отрицание, «НЕ»)

 |  |
| 0 | 1 |
| 1 | 0 |
Конъюнкция (логическое умножение, «И»)

 |  |  |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (логическое сложение, «ИЛИ»)

 |  |  |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Аналитическое представление логических функций
Дизъюнктивная нормальная форма

| X1 | X2 | f |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Конъюнктивная нормальная форма

| X1 | X2 | f |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Способы описания логических функций
Применяются следующие способы описания логических функций:
| Номер набора | f |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| X1 | X2 | X3 | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Пример числового описания логических функций


Пример аналитического описания логических функций
Пример координатного описания логических функций
Пример графического описания логических функций
Аксиомы алгебры логики
Аксиомы конъюнкции

Аксиомы дизъюнкции

Аксиомы отрицания
если 



Теоремы алгебры логики
Теоремы исключения констант

Теоремы идемпотентности (тавтологии, повторения)


Теорема противоречия

Теорема «исключённого третьего»

Теорема двойного отрицания (инволюции)

Законы алгебры логики
Ассоциативный (сочетательный) закон

Коммутативный (переместительный) закон

Дистибутивный (распределительный) закон


Законы де Моргана (законы общей инверсии или дуальности)


Закон поглощения (элиминации)

Закон склеивания (исключения)

Базисы и формы представления логических функций



Базис (функционально полный набор) – это множество логических функций, суперпозицией которых можно представить любую логическую формулу, т. е. полная система логических функций.
Базисы могут быть избыточными и минимальными. Например, система функций И, Или, НЕ (булев базис, базис Буля) – избыточный базис, так как при удалении из него некоторых функций (функции ИЛИ или функции И) система остаётся полной.
Минимальными базисами являются системы: 1) И, НЕ; 2) ИЛИ, НЕ; 3) И-НЕ (базис Шеффера); 4) ИЛИ-НЕ (базис Пирса). При удалении из таких базисов любой операции они перестают быть полными системами функций.
В табл. 2.9 приведено несколько полезных свойств булевых функций НЕ, И, ИЛИ, формулы перехода между базисами И-НЕ и ИЛИ-НЕ (законы де Моргана), а также формулы перехода от операций импликация, тождественность и сумма по модулю 2 в базис Буля. Все приведённые соотношения можно легко проверить с помощью их таблиц истинности.
Таблица 2.9
| № | Формулы булевой алгебры | Формулы в упрощённой записи | Название свойства |
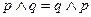 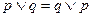 | 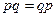 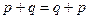 | Коммутативность (перемена мест операндов) | |
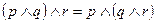  | 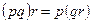 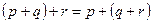 | Ассоциативность (последовательность выполнения операций) | |
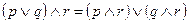 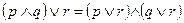 | 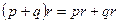 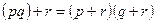 | Дистрибутивность (раскрытие скобок) | |
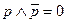 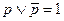 | 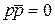 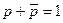 | Законы исключённого третьего | |
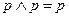 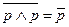 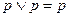 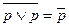 | 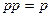 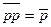 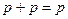 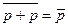 | Законы тождественных операндов | |
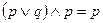 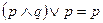 | 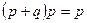 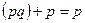 | Законы поглощения | |
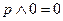 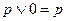 | 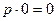 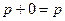 | Свойства нуля | |
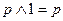 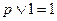 | 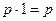 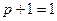 | Свойства единицы | |
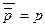 | Свойство двойного отрицания | ||
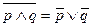 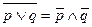 | 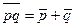 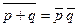 | Законы (формулы) де Моргана | |
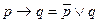 | 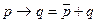 | Свойство импликации | |
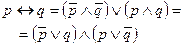 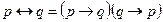 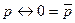 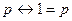 | 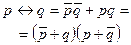 | Свойства эквивалентности | |
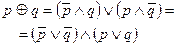 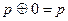 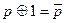 | 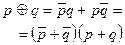 | Свойства сложения по модулю два |
Далее по возможности будем пользоваться упрощёнными обозначениями логических операций.
Докажем некоторые из приведённых свойств:
7. 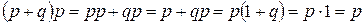
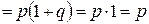
12. 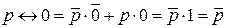
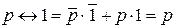
13. 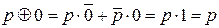
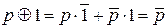
Введём понятие терма.
Терм – это дизъюнкция или конъюнкция любого числа переменных, взятых с отрицанием или без него. В терм в общем случае не обязательно должны входить все переменные, он даже может состоять только из одной переменной.
Термы, состоящие только из одной переменной, взятой с отрицанием или без него, называются первичными термами.
Ранг терма определяется количеством переменных, входящих в данный терм.
Терм в виде конъюнкции переменных, взятых с отрицанием или без него, называется конъюнктивным термом, конституентой единицы (любой такой терм, принимающий значение 1, автоматически приводит к единичному значению функции) или минтермом (для принятия функцией значения 1 требуется минимальное количество единичных термов, а точнее только один). Под минтермом обычно понимается конъюнктивный терм, содержащий все переменные логической функции.
Терм, являющийся дизъюнкцией логических переменных в прямом или инверсном виде, называется дизъюнктивным термом, конституентой нуля (любой такой терм, принимающий значение 0, автоматически приводит к нулевому значению функции) или макстермом (для принятия функцией значения 1 требуется максимальное количество единичных термов, а точнее всех термов). Под макстермом обычно понимается дизъюнктивный терм, содержащий все переменные логической функции.
Теорема 2.1. Любая логическая функция может быть представлена как суперпозиция только трёх функций: И, ИЛИ и НЕ.
Доказательство данной теоремы основано на лемме о дизъюнктивном разложении.
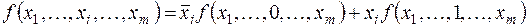
Действительно, при xi = 0 правая часть этой формулы принимает значение
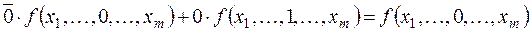
аналогично при xi = 1 правая часть
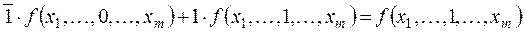
Итак, правая часть формулы (2.4) при всех наборах аргументов совпадает с левой, что доказывает справедливость формулы (2.4).
Таким образом, любую булеву функцию можно представить как дизъюнкцию термов, каждый из которых представляет собой конъюнкцию всех переменных (с отрицаниями или без них) и значения этой функции на соответствующем конкретном наборе значений переменных.
Примем для σ 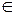
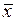
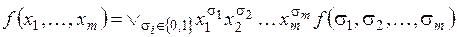
Поскольку значения функции на каждом конкретном наборе равны либо 0, либо 1, то в формуле (2.5) останутся только такие термы, которые соответствуют наборам переменных, на которых функция равна единице:
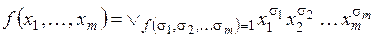
Представление булевой функции в форме дизъюнкции конъюнктивных термов (конституент единицы) Ki
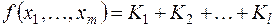
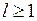
называется дизъюнктивной нормальной формой (ДНФ) этой функции.
Если все конъюнктивные термы в ДНФ являются минтермами, т. е. содержат в точности по одной все логические переменные, взятые с отрицаниями или без них, то такая форма представления функции называется совершенной дизъюнктивной нормальной формой (СДНФ) этой функции. СДНФ называется совершенной, потому что каждый терм в дизъюнкции включает все переменные; дизъюнктивной, потому что главная операция в формуле – дизъюнкция. Понятие “нормальной формы” означает однозначный способ записи формулы, реализующей заданную функцию.
С учётом сказанного выше из теоремы 2.1 вытекает следующая теорема.
Теорема 2.2. Любая булева функция ( не равная тождественно 0 ) может быть представлена в СДНФ, причём такое представление единственно.
Таблица 2.10
На основании формулы (2.6) получаем:
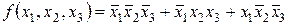
Как видно, при составлении СДНФ функции нужно составить дизъюнкцию всех минтермов, при которых функция принимает значение 1.
Представление булевой функции в форме конъюнкции дизъюнктивных термов (конституент нуля) Di
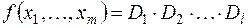
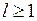
называется конъюнктивной нормальной формой (КНФ) этой функции.
Если все дизъюнктивные термы КНФ являются макстермами, т. е. содержат в точности по одной все логические переменные функции, взятые с отрицаниями или без них, то такая КНФ называется совершенной конъюнктивной нормальной формой (СКНФ) этой функции.
Теорема 2.3. Любая булева функция ( не равная тождественно 1 ) может быть представлена в СКНФ, причём такое представление единственно.
Доказательство теоремы может быть проведено аналогично доказательству теоремы 2.1 на основании следующей леммы Шеннона о конъюнктивном разложении.
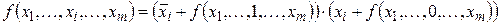
Нужно отметить, что обе формы представления логической функции (ДНФ и КНФ) теоретически являются равными по своим возможностям: любую логическую формулу можно представить как в ДНФ (кроме тождественного нуля), так и в КНФ (кроме тождественной единицы). В зависимости от ситуации представление функции в той или иной форме может быть короче.
В отличие от СДНФ, при составлении СКНФ в таблице истинности логической функции нужно смотреть комбинации переменных, при которых функция принимает значение 0, и составить конъюнкцию соответствующих макстермов, но переменные нужно брать с обратной инверсией:
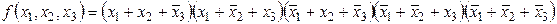
Нужно отметить, что непосредственно перейти от СДНФ функции к её СКНФ или наоборот невозможно. При попытке таких преобразований получаются функции, обратные по отношению к желаемым. Выражения для СДНФ и СКНФ функции непосредственно можно получить только из её таблицы истинности.
Используя результат примера 2.3 получим:
Как видно, под общей инверсией получилась СКНФ логической функции, которая является обратной по отношению к функции, полученной в примере 2.4:
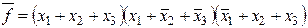
т. к. содержит все макстермы, которых нет в выражении для СКНФ рассматриваемой функции.
Далее приведём систематическую процедуру (алгоритм) преобразования аналитической записи функции в нормальную форму с использованием свойств булевых функций.
1. Используя свойства операций (см. табл. 2.9) тождественность ( 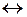
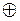
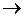
2. Используя свойства отрицания и законы де Моргана (см. табл. 2.9) добиваемся, чтобы операции отрицания относились только к отдельным переменным, а не к целым выражениям.
3. Используя свойства логических операций И и ИЛИ (см. табл. 2.9), получаем нормальную форму (ДНФ или КНФ).
4. При необходимости переходим к совершенным формам (СДНФ или СКНФ). Например, для получения СКНФ часто нужно использовать свойство: 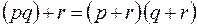
Пример 2.6. Преобразовать в СКНФ логическую функцию
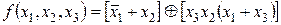
Выполняя по порядку шаги приведённого выше алгоритма, получим:
Используя свойство поглощения, получим: