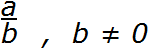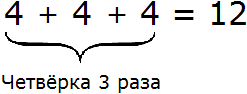Что такое основные операции
Операции в языке Си
Над объектами в языке Си могут выполняться различные операции:
Результатом выполнения операции является число.
Операции могут быть бинарными или унарными.
Бинарные операции выполняются над двумя объектами, унарные — над одним.
Операция присваивания
Операция присваивания обозначается символом = и выполняется в 2 этапа:
объект = выражение;
В случае если объекты в левой и правой части операции присваивания имеют разные типы используется операция явного приведения типа.
объект = (тип)выражение;
Операции отношения
Основные операции отношения:
Арифметические операции
Основные бинарные операции, расположенные в порядке уменьшения приоритета:
Основные унарные операции:
Результат вычисления выражения, содержащего операции инкрементирования или декрементирования, зависит от того, где расположен знак операции (до объекта или после него). Если операция расположена до объекта, то сначала происходит изменение значения переменной на 1, а потом это значение используется для выполнения следующих операций. Если операция ++ или — расположена после переменной, то сначала выполняется операция, а потом значение переменной изменяется на 1.
Бинарные арифметические операции могут быть объединены с операцией присваивания:
Логические операции
Логические операции делятся на две группы:
Условные логические операции чаще всего используются в операциях проверки условия if и могут выполняться над любыми объектами. Результат условной логической операции:
Вообще, все значения, отличные от нуля, интерпретируются условными логическими операциями как истинные.
Основные условные логические операции:
Побитовые логические операции оперируют с битами, каждый из которых может принимать только два значения: 0 или 1.
Основные побитовые логические операции в языке Си:
Для каждого бита результат выполнения операции будет получен в соответствии с таблицей.
a
a; // e = 241 = 1111 0001
f = a ^ b; // f = 7 = 0000 0111
| Бит | Маска |
| 0 | 0x01 |
| 1 | 0x02 |
| 2 | 0x04 |
| 3 | 0x08 |
| 4 | 0x10 |
| 5 | 0x20 |
| 6 | 0x40 |
| 7 | 0x80 |
Для установки определенного бита необходимо соответствующий бит маски установить в 1 и произвести операцию побитового логического ИЛИ с константой, представляющей собой маску:
Для сброса определенного бита необходимо соответствующий бит маски сбросить в 0 и произвести операцию побитового логического И с константой, представляющей собой инверсную маску:
0x02); // a = 1, бит 1 сброшен
Бинарные побитовые логические операции могут быть объединены с операцией присваивания:
Сдвиговые операции
Операции арифметического сдвига применяются в целочисленной арифметике и обозначаются как:
Общий синтаксис осуществления операции сдвига:
объект = выражение сдвиг КоличествоРазрядов;
Арифметический сдвиг целого числа вправо >> на 1 разряд соответствует делению числа на 2.
Арифметический сдвиг целого числа влево на 1 разряд соответствует умножению числа на 2.
Основные операции
Основные операции, которые используются в математике это сложение, вычитание, умножение и деление.
Ещё пример. Число 11 меньше, чем число 15. Эту фразу можно записать так:
В математике с помощью отношений можно записывать законы, формулы, уравнения и функции. Можно записать, что одно выражение равно другому, либо какое-то действие недопустимо по отношению к какому-нибудь объекту, числу, закону.
Например, знаменитая фраза «на ноль делить нельзя» записывается так:
Не будем опережать события и забегать вперёд. Просто скажем, что в этом выражении вместо a и b могут стоять любые числа. Но потом говорится, что b не должно быть равным нулю.
Знак равенства = стáвится между величинами и говорит о том, что эти величины равны между собой.
Ещё пример: если один большой арбуз весит 20 кг, а два маленьких арбуза весят по 10 кг каждый, то между арбузом в 20 кг и двумя арбузами по 10 кг можно поставить знак равенства. Это отношение можно прочитать так: «один арбуз весом в 20 килограмм равен весу двух арбузов, каждый из которых весит 10 кг». Ведь 20 кг = 10 кг + 10 кг.
Знак не равно ≠ ставится между величинами тогда, когда они не равны между собой.
Вы можете осмотреться вокруг себя и найти множество примеров отношений, которые можно истолковать с точки зрения математики.
Операция сложения
Операция сложения обозначается знаком «плюс» (+) и используется, когда складывают числа.
Числа, которые складывают называются слагаемыми. Число, которое получается в результате их сложения, называется суммой.
Например, сложим числа 3 и 2.
Записываем 3 + 2 = 5
В этом примере 3 − это слагаемое, 2 − второе слагаемое, 5 − сумма.
В будущем придётся складывать довольно большие числа. Но сложение этих больших чисел в конечном итоге будет сводиться к тому, чтобы сложить маленькие.
Поэтому нужно научиться складывать маленькие числа в диапазоне от 0 до 9. Например:
Можете потренироваться, записав в тетради несколько простых примеров. Поверьте, ничего постыдного в этом нет.
Операция вычитания
Операция вычитания обозначается знаком «минус» (−) и используется когда из одного числа вычитают другое.
Число, из которого вычитают другое число, называется уменьшаемым. Число, которое вычитают из уменьшаемого числа, называется вычитаемым. Число, которое получается в результате, называется разностью.
Например, вычтем из числа 10 число 2.
В этом примере число 10 − это уменьшаемое, число 2 − вычитаемое, а число 8 − разность.
Операция умножения
Обозначается знаком умножения (×) и используется когда одно число умножается на другое. Слово умножение говорит само за себя — какое-то число увеличивается в определенное количество раз, то есть мнóжится.
Например, запись 4 × 3 означает, что четверка в ходе операции умножения будет увеличена в три раза.
Число, которое увеличивают, называется множимым. Число, которое показывает во сколько раз нужно увеличить множимое, называется множителем. Число, которое получается в результате называется произведением.
Например, умножим число 4 на 3.
В этом примере 4 − это множимое, 3 − множитель, 12 − произведение.
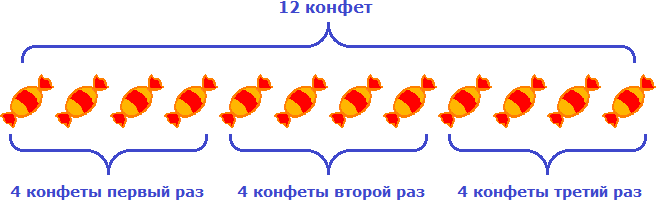
Запись 4 × 3 можно понимать как «повторить число 4 три раза». Например, если у нас имеются четыре конфеты и мы повторим их три раза, то полýчится двенадцать конфет:
Другими словами, умножение 4 на 3 можно представить как сумму трёх четвёрок:
Умножение можно понимать и другим образом, а именно как взятие чего-то определенное количество раз.
Допустим, в вазе лежат конфеты. Возьмём четыре конфеты один раз:
У нас в руках окажется четыре конфеты.
Попробуем взять четыре конфеты 2 раза:
У нас в руках окажется восемь конфет.
Попробуем взять четыре конфеты ноль раз, то есть ни разу:
У нас на руках не окажется конфет, поскольку мы ни разу их не взяли. Поэтому умножение любого числа на ноль даёт в ответе ноль.
В некоторых книгах множимое и множитель называют одним общим словом — сомножители. Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.
Операция деления
Обозначается знаком деления (÷ или : ) и используется когда делят числа.
Число, которое делят называют делимым. Число, которое указывает на сколько частей делят делимое, называется делителем. Число, которое получается в результате, называется частным.
Например, разделим число 10 на 2.
В этом примере число 10 − это делимое, число 2 − делитель, число 5 − частное.
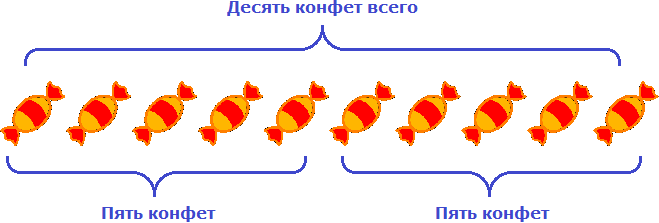
Если у нас имеются десять конфет и мы разделим их на две равные части, то в каждой части полýчится по пять конфет:
Так можно понять смысл записи 10 : 2 = 5.
Задания для самостоятельного решения
Большинство людей решат эти задания в уме что конечно похвально. Однако, рекомендуется выполнить эти задания именно в тетради, взяв в руку карандаш. К математике следует привыкать посредством решения простых примеров.
Основные логические операции
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
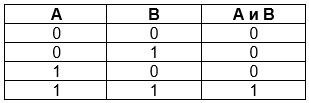
Таблица истинности для логического умножения выглядит так:
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
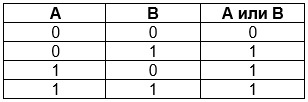
Таблица истинности логического сложения:
A, B — входная информация;
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Условное обозначение логического отрицания: с помощью частицы «не», символов ¯, \(\neg.\)
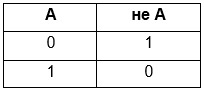
Таблица истинности инверсии:
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
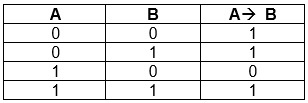
Таблица истинности для импликации:
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
По своему употреблению данная связка схожа со значением союзов «если. то. ».
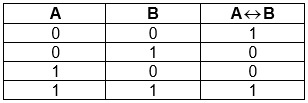
Логическая равнозначность (эквивалентность)
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
Таблица истинности для равнозначности:
Стрелка Пирса
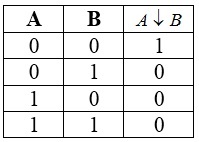
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Таблица истинности для этой операции следующая:
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
Штрих Шеффера
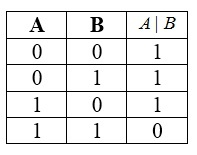
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
Для построения нужного порядка, как и в математических выражениях, используют скобки.
Основные типы хозяйственных операций в бухгалтерском учете
Хозяйственная операция в бухгалтерском учете — это…
Хозяйственная операция в бухгалтерском учете — это фиксирование фактов хозяйственной жизни предприятия. Отражение хозяйственных операций оказывает постоянное влияние на баланс активов и пассивов предприятия. Но ни одна хозяйственная операция не может нарушить его. Все фиксации деятельности происходят на основании первичных документов, заполненных в установленном порядке. Они и подтверждают факт совершенных операций.
Хозяйственные операции являются частью хозяйственного учета. Что собой представляет хозяйственный учет, читайте в статье «Хозяйственный учет — это. ».
Документирование хозяйственных операций и ведение бухучета
Важным элементом бухгалтерского учета является документирование. Его применяет каждое предприятие для наблюдения за своей хозяйственной деятельностью и первичного контроля. Документирование состоит из упорядоченного сбора первичных документов. Это является начальным этапом учета.
Первичный документ составляется в момент совершения той или иной хозяйственной операции. Существуют формы документов, которые утверждаются только законодательно, но основная масса — такие, которые может утвердить само предприятие. Каждый такой документ имеет юридическую силу и устанавливает ответственных за выполнение той или иной хозяйственной операции. Недопустимо принимать к бухгалтерскому учету документы, которыми оформляются несуществующие, мнимые сделки (ст. 9 закона «О бухгалтерском учете» от 06.12.2011 № 402-ФЗ).
Только наличие правильно оформленных первичных документов поможет предприятию отстаивать свои интересы в суде или гарантировать сохранность своего имущества. Правильное документирование хозяйственных операций можно использовать для объективного анализа результатов работы предприятия как его собственниками, так и налоговыми органами.
Отражение хозяйственных операций на счетах бухгалтерского учета
После того как первичные документы собраны и проверены, они фиксируются на счетах бухгалтерского учета в хронологическом порядке. Каждое событие финансово-хозяйственной деятельности имеет двойственный характер. Суть этой двойственности сводится к тому, что при записи одного события используется 2 счета бухучета, которые указывают на состав, место размещения имущества и источники его образования.
Как правильно отражать хозяйственные операции с использованием двойных записей, читайте в статье «Понятие и сущность двойной записи в бухгалтерском учете».
Связь этих счетов называется корреспонденцией, а сами счета корреспондирующими.
Отражение операций с использованием корреспонденции счетов называют бухгалтерской проводкой.
Подробнее о том, какие бывают проводки, читайте в статье «Основные проводки по бухучету — примеры».
Также рекомендуем справочник «16 700 БУХГАЛТЕРСКИХ ПРОВОДОК С КОММЕНТАРИЯМИ», который вы найдете в КонсультантПлюс, если получите бесплатный пробный доступ к системе.
Типы хозяйственных операций в бухгалтерском учете — примеры
Хозяйственные операции разделяют на 4 типа. Все они оказывают влияние на баланс, при этом равенство баланса не нарушается.
На расчетный счет ООО «Звезда» были перечислены денежные средства в размере 5 000 рублей в счет оплаты за полученный товар.
Проводка: Дт 51 Кт 62 — 5 000.
В результате такой операции валюта баланса осталась неизменной, изменения произошли только в статьях актива баланса. Статья «Расчетный счет» увеличилась на 5 000 рублей, а статья «Расчеты с покупателями и заказчиками» уменьшилась на эту же сумму.
ООО «Звезда» в конце отчетного периода получило прибыль. Участники общества решили рассчитать и начислить дивиденды в размере 10 000 руб.
Проводка: Дт 84 Кт 75 — 10 000.
В результате валюта баланса опять остается неизменной, а вот статьи пассива баланса изменились. Статья «Расчеты с учредителями» увеличилась, статья «Нераспределенная прибыль» уменьшилась на 10 000 руб.
На склад ООО «Звезда» поступили товары от поставщика ООО «Розмарин» на сумму 3 000 руб.
Проводка: Дт 41 Кт 60 — 3 000.
Результатом будет увеличение валюты баланса, т. к. в данном случае изменения произошли в обеих частях баланса (в активе и пассиве). Статья пассива «Расчеты с поставщиками и подрядчиками» и статья актива «Товары» были увеличены на 3 000 руб.
После того как товар был поставлен на склад, ООО «Звезда» произвела перевод денежных средств на расчетный счет ООО «Розмарин» в сумме 3 000 руб.
Проводка: Дт 60 Кт 51 — 3 000.
В результате валюта баланса снова изменилась, только в сторону уменьшения. Изменения произошли и в активе, и в пассиве баланса. Статья пассива «Расчеты с поставщиками и подрядчиками» и статья актива «Расчетный счет» уменьшились на 3 000 руб.
Итоги
Важно помнить, что каждая совершенная хозяйственная операция должна пройти путь от подтверждения ее первичным документом до отнесения к одному из 4 типов операций и получить свое отражение на счетах бухучета. Ни одна из операций при правильном ее оформлении не может нарушить равенство баланса.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!