Что такое острые углы

Острый угол

Острый угол — это угол, меньший прямого.

Градусная мера острого угла больше нуля, но меньше 90 градусов.

∠ABC, ∠MNK, ∠DEF — острые углы.

Чтобы построить острый угол заданной градусной меры, пользуются транспортиром.

Построить с помощью транспортира угол 72º.

1) Отмечаем точку — вершину угла.

2) От точки проводим луч — сторону угла.

3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей транспортира положение этой отметки может быть разным) так, чтобы отметка 0º была расположена на стороне угла.

4) Находим 72º на той шкале, где находится 0º, и ставим точку.

5) От вершины угла через отмеченную точку проводим луч — вторую сторону угла.

На рисунках изображено построение угла 72º с началом отсчёта по нижней шкале и с началом отсчёта по верхней шкале.

∠ABC=72º

∠CDE=72º

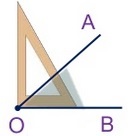
Чтобы определить по рисунку, является ли угол острым, можно воспользоваться угольником. Если приложить вершину угольника к вершине угла так, чтобы сторона угольника прошла через одну сторону угла, то другая сторона угольника закроет вторую сторону угла:

Источник

Острый угол

Какой угол называется острым в математике

Угол представляет собой геометрическую фигуру, которая образована с помощью пары лучей. Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.

Угол является геометрической фигурой, состоящей из пары лучей в виде ее сторон, которые выходят из одной точки или вершины.

Данные фигуры в геометрии подразделяют на типы в зависимости от градусной величины, расположению относительно друг друга и относительно окружности. Основными видами являются:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Градусная мера, которой обладает острый угол, менее 90 градусов. Данный вид геометрической фигуры можно встретить в каждом четырехугольнике, если он не является прямоугольным квадратом или произвольным параллелограммом. Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:

Определение, основные признаки и свойства

Острый угол – это геометрическая фигура, градусная мера которой составляет менее 90 градусов.

Для всех острых углов характерна градусная мера в интервале от 0 до 90 градусов. Простым способом распознавания типа угла является использование предмета, который имеет прямой угол. Его прикладывают к искомому элементу таким образом, чтобы их вершины были совмещены. Примером такого инструмента является линейка. Возможно два варианта результата измерений:

Точным инструментом для измерения градусной меры является транспортир, который состоит из линейки и полуокружности. Пользоваться им несложно. Достаточно приложить центр транспортира к вершине фигуры таким образом, чтобы любой из его сторон совпадал с гранью линейки. Второй луч покажет градусы, соответствующие геометрической фигуре.

Транспортир также применяют, когда необходимо начертить тупой или острый угол:

Особенности рассматриваемой геометрической фигуры:

Примеры решения задач

Задача 1

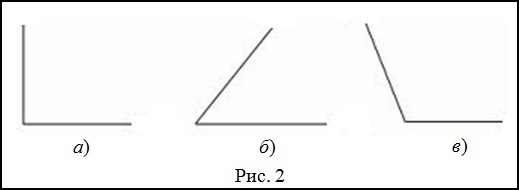
С помощью рисунка необходимо найти острые углы.

Решение

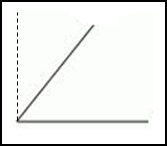
Стороны фигуры, изображенной на первом рисунке, перпендикулярны друг другу. Поэтому его нельзя назвать острым. На втором рисунке начерчен угол, который меньше, чем прямой.

Согласно определению, данный угол является острым. Если сравнить угол, который изображен на третьем рисунке, с прямым, то можно сделать вывод, что он тупой, так как его градусная мера составляет больше, чем 90 градусов.

Ответ: острым является угол, который изображен на втором рисунке.

Задача 2

Имеется пара смежных углов. Один из них больше, чем второй на 30 градусов. Требуется определить, какой из этих углов является острым.

Решение

Обозначим меньший угол буквой х. Тогда (х+30) является большим углом. Известно, что сумма смежных углов составляет 180 градусов. Можно записать справедливое равенство:

Источник

Определение острого угла

Вы будете перенаправлены на Автор24

Острый угол: определение

Помимо острых углов также существуют тупые и прямые углы. Прямой угол равен 90°, а если две прямые пересекаются под прямым углом, о них также говорят, что они перпендикулярны.

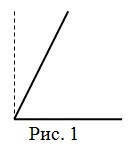
Рисунок 1. Как выглядит острый угол. Автор24 — интернет-биржа студенческих работ

Для того чтобы определить, является ли угол острым или тупым, достаточно приложить любой предмет, имеющий прямой угол к данному углу так, чтобы их вершины совпадали, например, линейку.

Если прямой угол полностью вмещает в себя нарисованный — то этот угол является острым, если же наоборот нарисованный угол помещает в себя прямой — то рассматриваемый угол тупой.

Более точно угол можно измерить с помощью транспортира. Транспортир — это инструмент, состоящий из линейки и полуокружности.

Для того чтобы им воспользоваться, нужно наложить центр транспортира на вершину угла, причём так, чтобы один из образующих угол лучей совпадал с гранью линейки.

Рисунок 2. Измерение острого угла. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Второй же луч укажет на значение угла.

Также с помощью транспортира можно построить острый или тупой угол: для этого нужно нарисовать один из лучей, затем разместить его начало в центре транспортира, приложить линейку к необходимому числу градусов и провести по ней линию.

Особенности острых углов

Какой из углов не является острым?

Рисунок 3. Углы. Автор24 — интернет-биржа студенческих работ

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 04 2021

Источник

Что такое острые углы

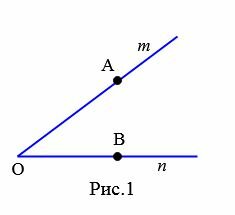
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)

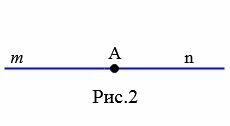
Развернутый угол. Внутренняя и внешняя область угла

Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

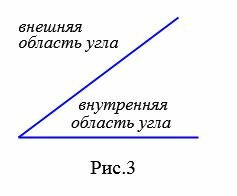
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

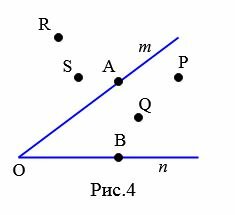Типы углов

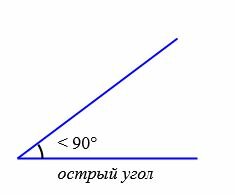
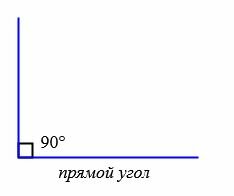
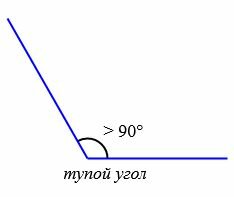
В зависимости от величин, углы бывают следующих типов (Рис.5):

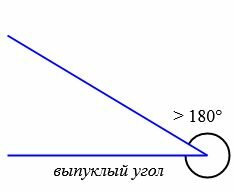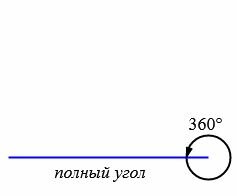Сравнение углов

Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

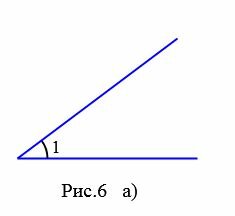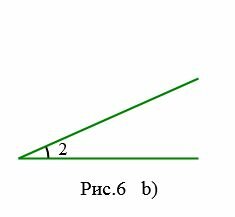На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)

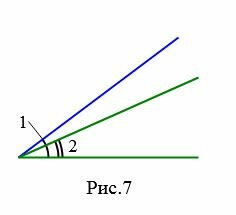Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Источник

Виды углов

Содержание

В прошлом уроке мы познакомились с понятием угла, теперь настало время узнать, какие виды углов существуют.

Равные углы

Возьмём лист бумаги и изобразим на нём угол DEF. Теперь сложим листок так, чтобы лучи ED и EF совпали, и по полученному сгибу проведём луч EG.

Рисунок 1

Так как совпадают стороны угла DEF, то совпадают ∠DEG и ∠FEG.

Если два угла совпадают при наложении, то они называются равными.

Равенство углов записывается так: ∠DEG=∠FEG.

Для обозначения равенства углов на рисунке проводят равное количество дужек.

Рисунок 2

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Тогда на рисунке 2 луч BD – биссектриса угла ABC.

Неравные углы

Изобразим угол КON и проведём произвольный луч ОР. По рисунку 3 видно, что при наложении углы КОP и NОР не совпадут.

Рисунок 3

Если два угла не совпадают при наложении, то они не равны друг другу и называются неравными.

Неравенство углов записывается так: ∠ КОP≠∠NОР

Для обозначения неравенства углов на рисунке изображают разное количество дужек.

Рисунок 4

Развёрнутый угол

Рассмотрим рисунок 5. Лучи ML и MN дополняют друг друга до прямой, поэтому называются дополнительными лучами.

Рисунок 5

Два дополнительных друг другу луча образуют развёрнутый угол.

Стороны такого угла вместе составляют прямую линию, на которой лежит вершина развёрнутого угла.

Развёрнутый угол – это угол, стороны которого образуют прямую.

Прямой угол

Возьмём лист бумаги и дважды сложим его пополам. Развернув лист, можно увидеть линии сгиба, которые образовывают 4 равных угла.

Рисунок 6

Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми и на рисунках обозначаются знаком “∟”.

Прямой угол – это половина развёрнутого угла.

Для построения прямого угла используют чертёжный треугольник.

Рисунок 7

Острые и тупые углы

Острый угол – угол, который меньше прямого угла.

Тупой угол – угол, который больше прямого, но меньше развёрнутого угла.

На рисунке 8 изображён острый угол ABC и тупой угол DEF.

Рисунок 8

Источник