Что такое отношение катета к гипотенузе

Синус, косинус, тангенс в прямоугольном треугольнике

Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.

Подробнее про прямоугольный треугольник здесь.

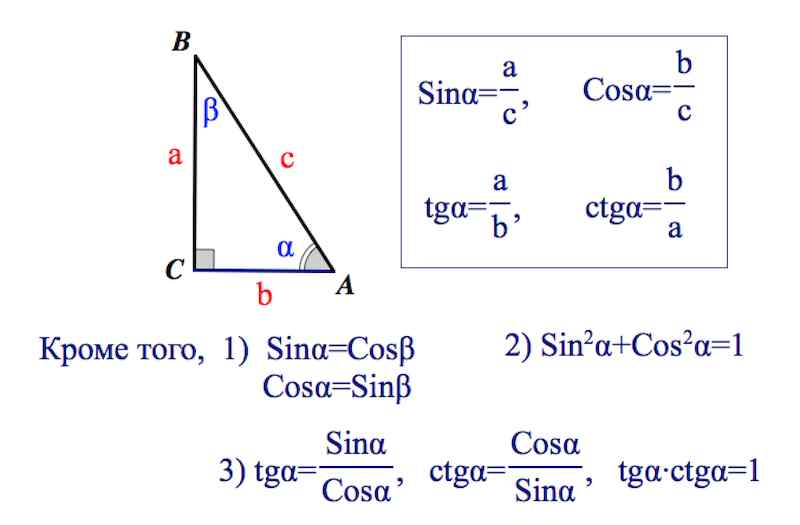
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.

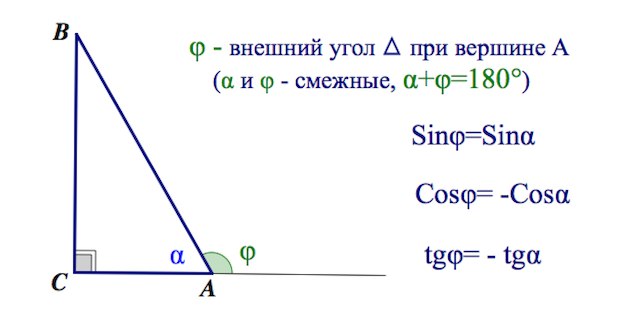
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):

Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Как навсегда запомнить, что такое синус и косинус, и никогда больше не ошибаться и не путать их

Большая проблема всех детей в школе, когда они начинают изучать тригонометрию и знакомиться с синусами и косинусами — это не перепутать их. Многие помнят, что синус и косинус — это отношение катета к гипотенузе. Но катета два: прилежащий и противолежащий. И что из этого что?

Синус — это отношение прилежащего катета к гипотенузе? Или противолежащего? А косинус? Разобраться в этом раз и навсегда, запомнить, что к чему, поможет мнемоническое правило, которое мне рассказала одна очень хорошая учительница.

Итак, имеем прямоугольный треугольник, у которого два катета a и b, гипотенуза с. Угол между гипотенузой с и катетом b назовем ∠α.

У этого угла есть синус и косинус. В школе обычно говорят, что надо запомнить/зазубрить/выучить, что sinα = a/c, cosα=b/c.

Но зазубривание — это не очень надежный способ запоминания. Поэтому смотрим на схему ниже, которая позволит вспомнить, что такое синус или косинус в любое время.

У нас есть «О» и в слове «прОтиволежащий», и в кОсинусе. И есть буква «И» и в слове «прИлежащий», и в сИнусе. Так вот в каждой паре у нас должна быть и «И», и «О», поэтому сИнус — это отношение прОтиволежащего угла к гипотенузе, а кОсинус — прИлежащего к гипотенузе.

На первый взгляд может показаться, что это какое-то дурацкое правило, которое только путает, но если вы один раз разобрались и запомнили схему, которую я нарисовал выше, вы уже теперь никогда в жизни не забудете, что такое синус и косинус, и что самое важное — не перепутаете их. Так что запоминайте сами, рассказывайте детям и заходите на мой Ютуб канал.

Источник

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

Тангенс

Тангенс (tg) — это отношение синуса к косинусу (tgα = sinα / cosα). Либо отношение противолежащего катета (дальнего/противоположного) к прилежащему (который находится рядом с углом).

В этом треугольнике тангенс угла вычисляется по этой формуле:

Обратите внимание, что в вычислении принимают участие только катеты, гипотенузы здесь нет (противолежащий делится на прилежащий — это тангенс острого угла прямоугольного треугольника).

Вычислите длину стороны BC, зная, что tan α = 0,4:

tan α = противолежащий катет / прилежащий катет = BC / AB = x / 15

x / 15 = 0,4 x = 15 * 0,4 x = 6

Таблица тангенсов и котангенсов (главных углов от 0° до 360°)

α градусов	0°	30°	45°	60°	90°	180°	270°	360°
α радиан	0	π/6	π/4	π/3	π/2	π	3π/2	2π
tg α	0	√3/3	1	√3	–	0	–	0
ctg α	–	√3	1	√3/3	0	–	0	–

Основные тригонометрические тождества

Что такое синус?

Синус угла (sin) — это отношение противолежащего катета (который находится напротив угла) к гипотенузе (самой длинной стороне, находится напротив прямого угла).

В нашем примере sin α = BC/AC.

Что такое косинус?

Косинус угла (cos) — это отношение прилежащего катета (находится рядом с углом) к гипотенузе (самой длинной стороне, находится напротив прямого угла). В нашем примере cos α = AB/AC.

Что такое котангенс?

Котангенс угла (ctg) — это отношение прилежащего катета (который находится рядом с углом) к противолежащему (напротив угла). В нашем примере ctg α = AB / BC. Обратите внимание, что котангенс — это как «тангенс наоборот» (прилежащий делится на противолежащий), т. е. ctg α = AB / BC, а tg α = BC / AB (противолежащий делится на прилежащий).

Что такое секанс?

Секанс (sec или sec x) — это отношение гипотенузы (самой длинной стороны, напротив прямого угла) к прилежащему катету (рядом с углом) острого угла в прямоугольном треугольнике. Ещё секанс определяется формулой:

Что такое гипотенуза и катет?

Гипотенуза — это та сторона, которая находится напротив прямого угла (она самая длинная), в нашем треугольнике это сторона AC. Катеты — это две другие стороны, которые находятся рядом с прямым углом, в нашем треугольнике это стороны BC и AB:

Источник

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).