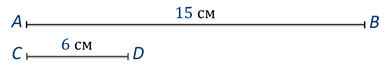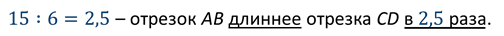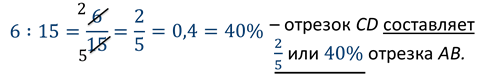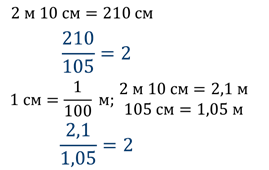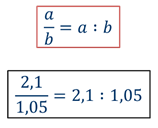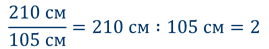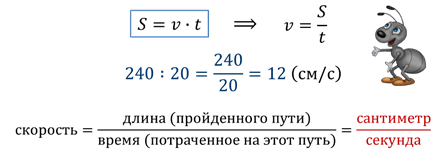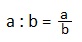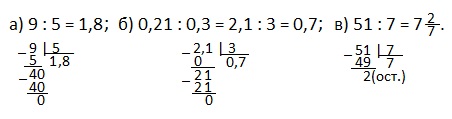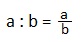Что такое отношение между числами
Отношение (математика)
Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.
Отношение может также означать результат операции деления, например:
Содержание
Формальное определение
n-местным (n-арным) отношением, заданным на множествах 
Иногда понятие отношения определяется только для частного случая 

Арность
Примеры
Отношения и предикаты
Отношение также может быть задано предикатом на n-й декартовой степени множества M: n-ка принадлежит отношению тогда и только тогда, когда предикат на ней возвращает значение 1 (или «истинно»). Таким образом, можно дать альтернативное определение отношения: если задано отображение 


Предикаты, которые формируются из отношений, заданных в соответствии с основным определением (когда множества в прямом произведении различны), используются в многосортном исчислении предикатов. [1]
Операции с отношениями
Система отношений, сформированная на одном и том же прямом произведении множеств, изоморфна алгебре множеств и допускает применение теоретико-множественных операций и проверок включения одного отношения в другое. Элементами множеств в этом случае являются кортежи элементов (n-ки).
Для отношений, у которых это ограничение не выполняется, теоретико-множественные операции не применимы, но возможны такие операции как соединение и композиция, которые используются в алгебре Кодда, алгебре кортежей и реляционной алгебре.
См. также
Примечания
Полезное
Смотреть что такое «Отношение (математика)» в других словарях:
Отношение (логика) — У этого термина существуют и другие значения, см. Отношение. Отношение в логике первого порядка двух и более аргументный предикат (многоместный предикат), двух и более предикатное свойство. Знак отношения: R.[уточнить] В терминах отношений… … Википедия
МАТЕМАТИКА — наука, или группа наук, о познаваемых разумом многообразиях и структурах, специально – о математических множествах и величинах; напр., элементарная математика – наука о числовых величинах (арифметика) и величинах пространственных (геометрия) и о… … Философская энциклопедия
ОТНОШЕНИЕ — в логике то, что в отличие от свойства характеризует не отдельный предмет, а пару, тройку и т.д. предметов. Традиционная логика не рассматривала О.; в современной логике О. пропозициональная функция от двух или большего числа переменных. Бинарным … Философская энциклопедия
МАТЕМАТИКА — Между духом и материей посредничает математика. Хуго Штейнхаус Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. Джордж Сантаяна Он стал поэтом для математика у него не хватало фантазии. Давид Гильберт об одном… … Сводная энциклопедия афоризмов
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
МАТЕМАТИКА — наука о количественных отношениях и пространственных формах действительного мира. В неразрывной связи с запросами техники и естествознания запас количественных отношений и пространственных форм, изучаемых М., непрерывно расширяется, так что это… … Математическая энциклопедия
Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия
Математика майя — Цифры майя Математика майя в своей основе использовала двадцатеричную систему счисления для записи чисел. Вычисления производились на специальном приспособлении (наподобие абака), счётными единицами которых служили какао бобы или различные по… … Википедия
Математика. 6 класс
Конспект урока
Отношение чисел и величин
Перечень рассматриваемых вопросов:
Частное двух не равных нулю чисел a и b называется отношением чисел a и b.
Числа a и b называются членами отношения.
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Отношение величин одного наименования (длин, скоростей, стоимостей и т. д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.
Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т. д.) есть новая величина.
Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.
Цена товара – это отношение стоимости товара к количеству единиц товара.
Теоретический материал для самостоятельного изучения
Отношения чисел и величин мы с вами встречаем не только в математике, но в географии. Давайте же разберёмся с этим понятием и научимся его использовать.
Частное двух не равных нулю чисел a и b называют отношением числа a к числу b.
Числа a и b называют членами отношения.
Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.
Мешок с красными яблоками весит 20 кг, а мешок с зелёными весит 10 кг. Во сколько раз мешок с красными яблоками тяжелее мешка с зелёными? Какую часть от красных яблок составляют зелёные?
Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма) есть новая величина.
Цена товара – это отношение стоимости товара к его количеству единиц товара.
За 4 шоколадки заплатили 48 рублей. Сколько стоит одна шоколадка?
Так как цена всей покупки составила 48 рублей, а купили мы 4 шоколадки, для нахождения цены одной шоколадки, нужно всю цену разделить на количество шоколадок.
Разбор заданий тренировочного модуля
№ 1. Ввод с клавиатуры пропущенных элементов в тексте.
Впишите ответ. Садовый участок имеет прямоугольную форму, его площадь равна 1000 кв. м. Длина участка равна 100 м. Найдите отношение длины участка к его ширине.
№ 2. Единичный / множественный выбор.
Отношение. Процентное отношение двух чисел
Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.
Отношение двух чисел показывает:
Процентное отношение
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Примеры.
Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1 200 изделий – это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 – 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2) На сколько процентов перевыполнен план?
Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Приведите отношение дробных чисел к отношению натуральных чисел.
В классе 25 учеников, 40% из них – девочки. Сколько девочек в классе?
В саду растет 5 кустов желтых роз, что составляет 25 % всех посаженных в саду кустов роз. Сколько всего кустов роз высажено в саду?
На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке?
Турист проехал до базы отдыха 80 км, что составляет 40 % всего расстояния. Сколько километров осталось преодолеть туристу до базы?
Сплав содержит 20% железа и 40% меди, остальное – бронза. Определите массу бронзы, если масса сплава составляет 5 кг.
Отношения
Урок 20. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Отношения»
Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.
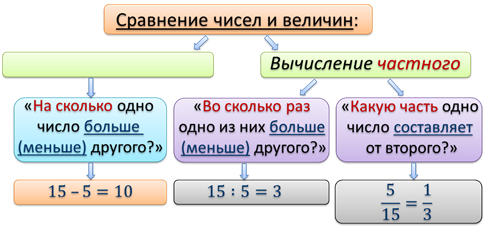
Для сравнения чисел и величин существуют, как вы знаете, два способа:
1-ый: вычисление разности и 2-ой: вычисление частного.
Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.
На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?
Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?
Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением.
Частное двух не равных нулю чисел (или двух величин) называют отношением.
Сами эти числа (величины) называют членами отношения.
Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.
Частные чисел читают так:
Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.
Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.
Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?
Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.
Итак, если а и b – любые числа, то
Сделаем важное замечание:
Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.
Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.
Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.
Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.
А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.
Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.
Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.
В виде отношений определяются и другие величины:
Из основного свойства частного следует свойство отношения.
Давайте вспомним основное свойство частного:
если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Следовательно, получаем свойство отношения:
отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.
Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.
Сами эти числа (величины) называют членами отношения.
Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
6.1. Отношение
I. Частное двух чисел называют отношением этих чисел.
так с помощью букв записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член. (Напоминание: дробная черта означает знак деления).
Примеры.
1) Найти отношения: а) 9 : 5; б) 0,21 : 0,3; в) 51 : 7.
Решение. Выполняем деление.
2) Найти неизвестные члены отношений: а) х : 6 = 24; б) 35 : х = 0,07.
Решение.
а) х : 6 = 24. Делимое равно х, делитель равен 6, частное равно 24. Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
х = 24 · 6;
х = 144.
б) 35 : х = 0,07. Делимое равно 35, делитель равен х, частное равно 0,07. Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 35 : 0,07;
х = 3500 : 7;
х= 500.
II. Если члены данного отношения переставить местами, то получившееся отношение называют обратным для данного отношения.
III. Отношение не изменится, если оба члена отношения умножить или разделить на одно и то же число, отличное от нуля.
В самом деле, отношение означает деление.
Члены отношения — это числитель и знаменатель обыкновенной дроби.
А мы знаем основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель умножить или разделить на одно и то же натуральное число.
Примеры.
3) Сократите отношение: а) 80 : 5; б) 42 : 45.
а) 80 : 5. Разделим оба члена этого отношения на 5. Тогда вместо числа 80 получим число 16 (80:5=16), а вместо числа 5 получим число 1 (5:5=1). Запишем: 80 : 5 = 16 : 1. Читают: восемьдесят так относится к пяти, как шестнадцать относится к единице.
б) 42 : 45. Каждый член этого отношения разделим на 3,
тогда получим равенство: 42 : 45 = 14 : 15. Читают: сорок два так относится к сорока пяти, как четырнадцать относится к пятнадцати.