Что такое отрезок с концами
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
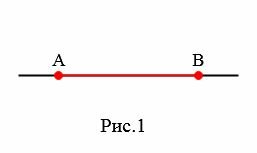 |
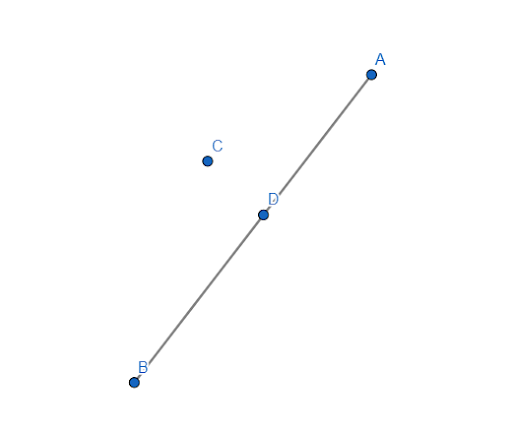
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
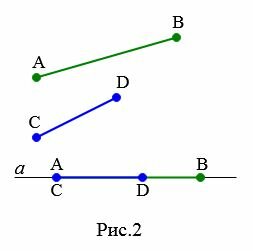 |
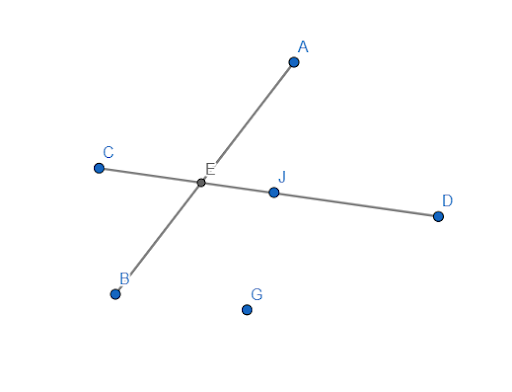
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
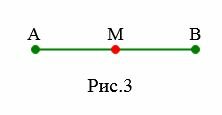 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
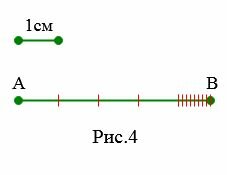 |
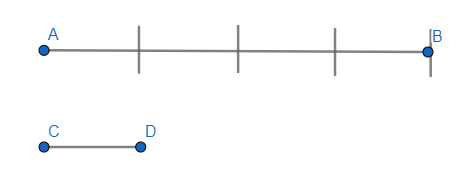
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
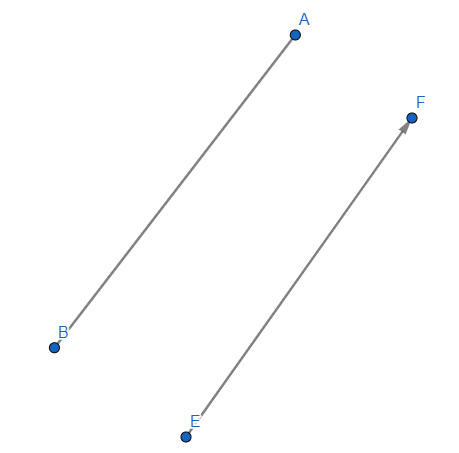
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
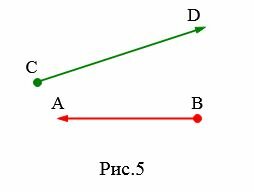 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Отрезок — что это такое
Что такое отрезок? Ответ на этот вопрос кажется весьма простым, когда вы учитесь в школе. Но с возрастом школьный курс математики постепенно забывается настолько, что такие простые вещи становятся не столь очевидными.
Отрезок — что это за фигура
Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.
Отрезок — это составная часть прямой, расположенная между двумя точками.
Вы можете дать определение также исходя из структурного подхода:
Отрезок — это такая математическая фигура, которая состоит из следующих элементов:
С этими составными частями вы можете ознакомиться на слайде:
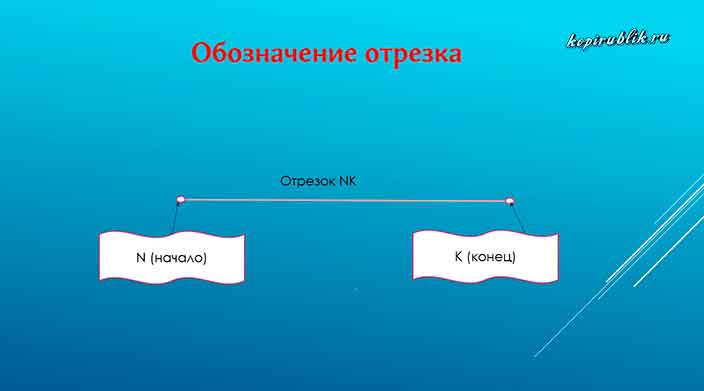
В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.
Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.
Важная характеристика, которая присуща любому отрезку – его длина.
Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.
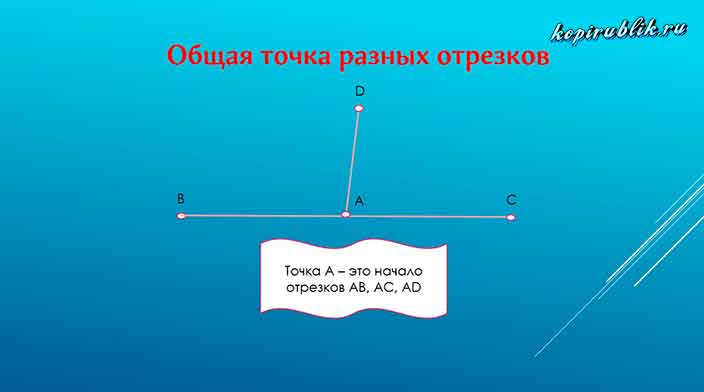
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.
Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.
Сравнение отрезка с геометрическими фигурами
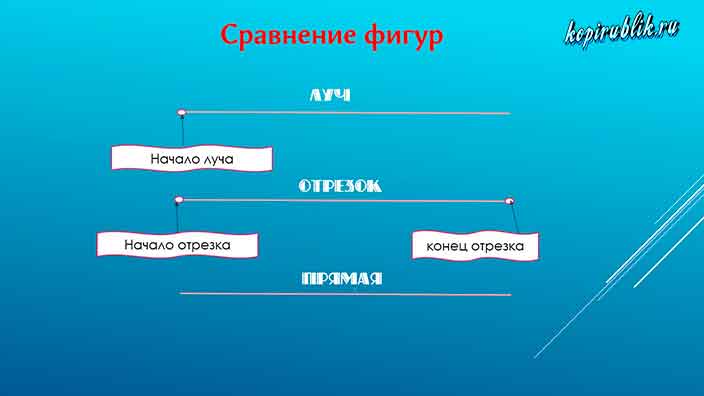
В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.
Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.
Луч — составная часть прямой, которая ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.
Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.
Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.
Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:
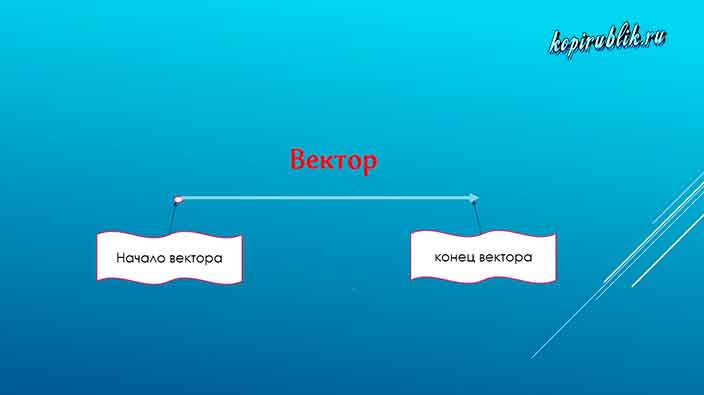
Направленный отрезок
В статье вы увидели базовый вид отрезка — ненаправленный. Это отрезок, у которого невозможно определить, что является его началом, а что — концом.
Существует второй вид отрезков – направленные.
Альтернативное название этой математической фигуры — вектор.
Особенностью направленного отрезка является то, что одна из точек, ограничивающих его длину, обозначается стрелкой. Она указывает, что именно там находится конец. Соответственно часть вектора, обозначенная точкой — это его начало.
Характерной чертой вектора является то, что он может быть описан не только двумя латинскими буквами, но и одной маленькой буквой, над которой располагается стрелка.
Направленный отрезок вместо показателя длины имеет характеристику — модуль, которая измеряется величинами, измеряющими расстояние – миллиметр, сантиметр, метр, километр.
В процессе работы с отрезками возникает вопрос: «Как рассчитать модуль вектора с использованием системы координат?».
Вы определите его следующим образом:
Направленные отрезки, которые лежат на одной прямой или параллельных прямых – это коллинеарные направленные отрезки.
Направленные отрезки, расположенные на параллельных прямых – это коллинеарные направленные отрезки.
Нулевой вектор — это отрезок, у которого одна точка включает начало и его конец.
Отрезки, соединённые в ломаную линию
Ломаная линия — это совокупность соединённых между собой отрезков, в которой окончание одного отрезка совпадает с начальной точкой другого. Каждая из составных частей ломаной линии называется звеном.
Ломаная линия содержит три типа вершин — точек, из которых состоят отрезки:
Первое и последнее звенья фигуры имеют по одной точке, которую они не делят с другими звеньями, а все остальные точки являются одновременно концом одного отрезка и началом другого, поэтому количество точек ломаной линии всегда на одну больше числа составляющих её отрезков.
Сравнение отрезков
Сравнить два отрезка — это значит сделать вывод о том, одинаковы ли они, или один по размеру больше другого.
Если наложить один отрезок на другой и они совпадут — это значит, что фигуры равны.
Наложение не всегда является возможным, поэтому для сравнения размеров отрезков вы можете использовать циркуль или линейку.
Отрезок: разные значения слова
Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке.
Часто слово употребляется для характеристики временного промежутка — «отрезок времени»
Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.
Как определяется понятие «отрезок» в геометрии
Содержание:
Для изображения прямых, лучей и отрезков применяют линейку. Отрезок на листике бумаги можно изобразить полностью, для луча и прямой – их фрагменты, ведь первый не имеет конца, только начало, вторая – бесконечна. Объясним, что такое отрезок в геометрии, чем отличается от иных фигур в евклидовом пространстве. Разберёмся с его свойствами.
Как выглядит отрезок
Обозначается двумя буквами – это название точек, лежащих в начале и конце. AB – концы геометрической фигуры, а расстояние между ними – длина фигуры, обозначается |AB|, измеряется преимущественно в сантиметрах.
Количество первых и вторых может быть любым.
Различают следующие отрезки:
Выше показаны расположенные в одной точке пересекающиеся отрезки, имеющие общую точку – E. Два обрезка не могут иметь больше одной общей точки.
Разнообразие и измерение отрезков
Геометрическая фигура AB тождественна или равная BA. Началом и концом может быть любая буква A или B, разницы нет. В случае с вектором фигура EF не равная FE.
Измерение геометрических фигур основано на аксиоме Архимеда: дана пара отрезков разной длины, причём AB > CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.
CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.» src=»https://455811.selcdn.ru/BINGOCDN/default/moddocument/3023/e374aa7c42abc85c5922eca722ecfd2f1c4ee8aa.png» />
На практике их длина измеряется линейкой. Начальная точка совмещается с обозначением ноля на именительном приборе, точность которого равна одному миллиметру. Если конечная точка лежит между рисками на линейке, разницу в доли миллиметра не учитывают – значение округляют.
При измерении бывают следующие случаи (при условии, что AB > CD):
В подобных случаях обходятся избыточным и недостаточным измерениями. В первом – дробь округляют в меньшую сторону: если получается более 5,6, записывают 5,6; во втором – 5,7 см.
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.