Что такое отрезок в математике 5 класс правило
Отрезок — что это такое
Что такое отрезок? Ответ на этот вопрос кажется весьма простым, когда вы учитесь в школе. Но с возрастом школьный курс математики постепенно забывается настолько, что такие простые вещи становятся не столь очевидными.
Отрезок — что это за фигура
Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.
Отрезок — это составная часть прямой, расположенная между двумя точками.
Вы можете дать определение также исходя из структурного подхода:
Отрезок — это такая математическая фигура, которая состоит из следующих элементов:
С этими составными частями вы можете ознакомиться на слайде:
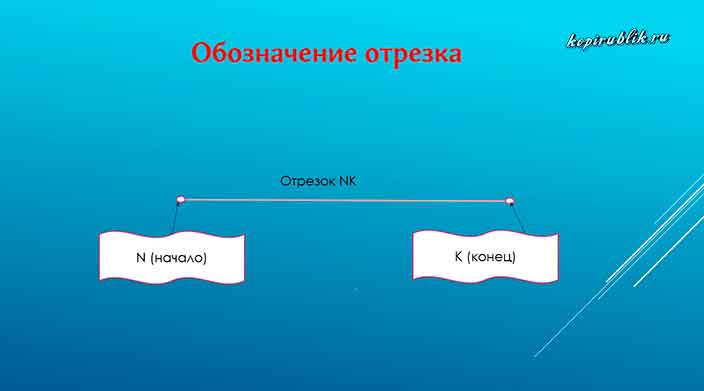
В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.
Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.
Важная характеристика, которая присуща любому отрезку – его длина.
Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.
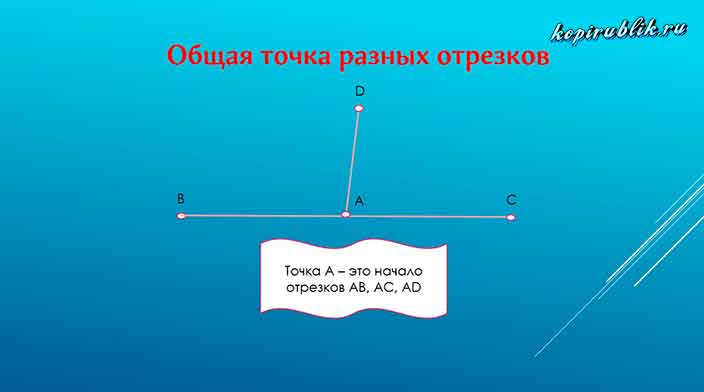
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.
Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.
Сравнение отрезка с геометрическими фигурами
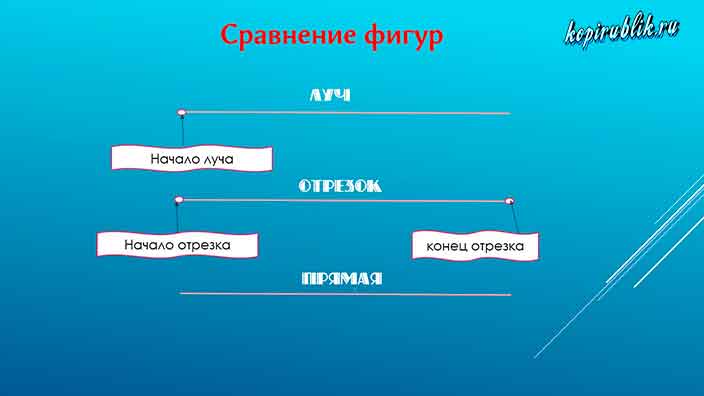
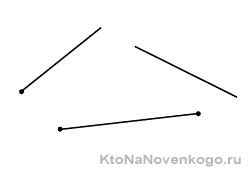
В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.
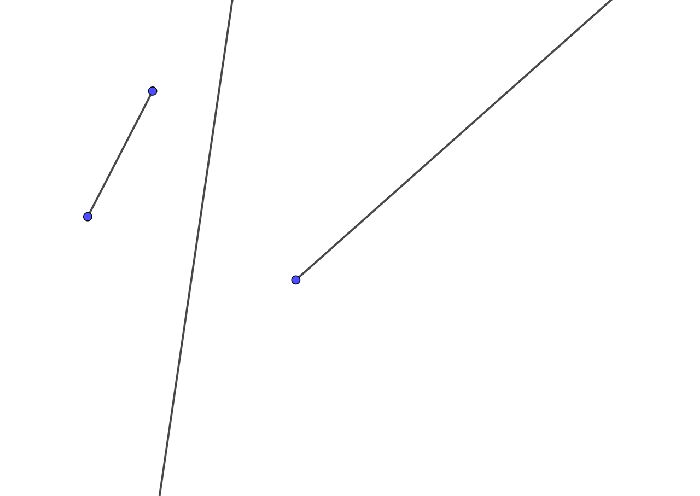
Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.
Луч — составная часть прямой, которая ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.
Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.
Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.
Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:
Направленный отрезок
В статье вы увидели базовый вид отрезка — ненаправленный. Это отрезок, у которого невозможно определить, что является его началом, а что — концом.
Существует второй вид отрезков – направленные.
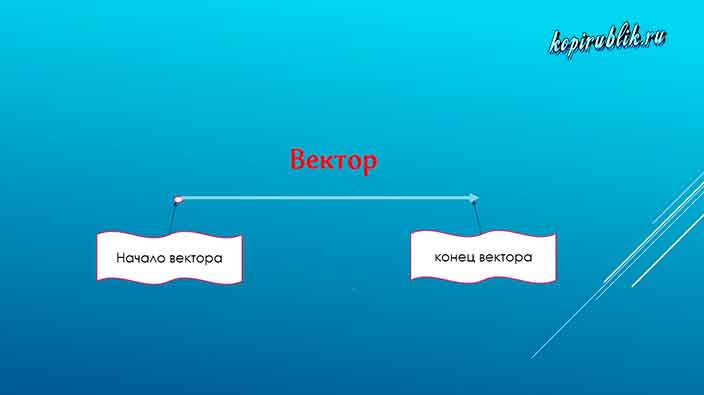
Альтернативное название этой математической фигуры — вектор.
Особенностью направленного отрезка является то, что одна из точек, ограничивающих его длину, обозначается стрелкой. Она указывает, что именно там находится конец. Соответственно часть вектора, обозначенная точкой — это его начало.
Характерной чертой вектора является то, что он может быть описан не только двумя латинскими буквами, но и одной маленькой буквой, над которой располагается стрелка.
Направленный отрезок вместо показателя длины имеет характеристику — модуль, которая измеряется величинами, измеряющими расстояние – миллиметр, сантиметр, метр, километр.
В процессе работы с отрезками возникает вопрос: «Как рассчитать модуль вектора с использованием системы координат?».
Вы определите его следующим образом:
Направленные отрезки, которые лежат на одной прямой или параллельных прямых – это коллинеарные направленные отрезки.
Направленные отрезки, расположенные на параллельных прямых – это коллинеарные направленные отрезки.
Нулевой вектор — это отрезок, у которого одна точка включает начало и его конец.
Отрезки, соединённые в ломаную линию
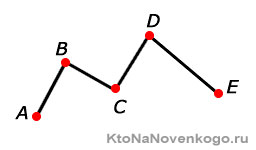
Ломаная линия — это совокупность соединённых между собой отрезков, в которой окончание одного отрезка совпадает с начальной точкой другого. Каждая из составных частей ломаной линии называется звеном.
Ломаная линия содержит три типа вершин — точек, из которых состоят отрезки:
Первое и последнее звенья фигуры имеют по одной точке, которую они не делят с другими звеньями, а все остальные точки являются одновременно концом одного отрезка и началом другого, поэтому количество точек ломаной линии всегда на одну больше числа составляющих её отрезков.
Сравнение отрезков
Сравнить два отрезка — это значит сделать вывод о том, одинаковы ли они, или один по размеру больше другого.
Если наложить один отрезок на другой и они совпадут — это значит, что фигуры равны.
Наложение не всегда является возможным, поэтому для сравнения размеров отрезков вы можете использовать циркуль или линейку.
Отрезок: разные значения слова
Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке.
Часто слово употребляется для характеристики временного промежутка — «отрезок времени»
Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.
Что такое отрезок
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.
Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.
Отрезок — это геометрическая фигура
Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.
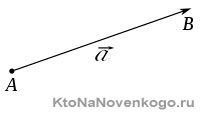
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.
В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.
Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.
Разница между отрезком, лучом и прямой
Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:
Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Направленный отрезок — это вектор
Отрезки бывают двух видов:
Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.
Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ ➜ и ВА ➜ — разные отрезки, так как они противоположно направленные.
Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.
Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.
Ломаная линия — это множество соединенных отрезков
Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.
Вершинами ломаной являются следующие точки:
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.
Любая замкнутая ломаная является геометрической фигурой — многоугольником.
Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.
Отрезок времени
Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.
Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.
Время в целом в таком случае определяется как временная прямая.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Чтобы не путать с лучом, надо просто запомнить, что отрезок — это две точки. То есть эта прямая и на ней две точки — это и называется отрезком.
Это самая простая часть геометрии и надо просто внимательно читать.
Жизнь тоже можно разделить на отрезки и все они будут неотделимо связаны с временем и конкретным человеком.
Что такое отрезок в математике?

Всего получено оценок: 157.
Всего получено оценок: 157.
Отрезок – это часть прямой. В математике тема отрезков имеет большое значение: из них составляют фигуры, с помощью отрезков чертятся рисунки к задачам и сравниваются числа. Поговорим о отрезках и способах их использования в математике 5 класса.
Определение
Отрезок – это часть прямой, ограниченный двумя точками. Это значит, что в отличие от прямой или луча, отрезок конечен и не имеет направления. Числовой отрезок на числовом луче или числовой прямой означает конкретное число. С помощью числовых отрезков можно выполнять сравнение чисел.
Числовой луч обычно принимается для сравнения положительных чисел. Если среди ряда чисел, которые необходимо сравнить, есть отрицательные значения – правильнее будет воспользоваться числовой прямой.
Отрезок всегда имеет определенное значение. Прямую или луч нельзя определить конечным числом в метрах или сантиметрах, поэтому во всех современных подсчетах, как теоретических, так и практических, используются отрезки.
Задача на построение
Построим треугольник со сторонами 3, 5 и 4. Каждая из сторон это отрезок заданной величины. Это еще одно из свойств отрезков. По трем отрезкам заданной величины всегда можно построить треугольник.
Для начала проведем отрезок АВ=3. Можно выбрать и любую другую величину из заданных.
Конкретно в этой задаче такой подбор чисел выполнен для возможности дальнейшей проверки.
Примем точку А за центр окружности с радиусом 4 и проведем ее. Затем примем точку В за центр окружности с радиусом 5. В точке пересечения двух окружностей мы получим точку С – третью точку треугольника.
Треугольник со сторонами 3, 4 и 5 – это классический прямоугольный треугольник. Соответственно с катетами 3, 4 и гипотенузой 5. Эти пропорции были выведены еще в Древней Греции и сегодня очень часто применяются в простых задачах на решение прямоугольных треугольников.
Конкретно в нашем случае это означает, что получившийся треугольник должен быть прямоугольным по теореме, обратной теореме Пифагора.
25=25 – все верно, условие выполняется. И на рисунке визуально понятно, что треугольник построен правильно. В случае построения произвольного треугольника по трем заданным отрезкам, убедитесь заранее, что выполняются условия неравенства в треугольнике: сторона всегда меньше суммы двух других сторон.
Задача с числовым лучом
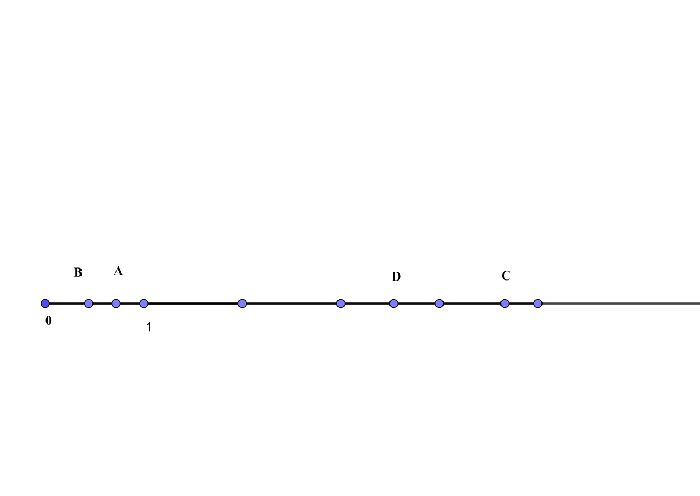
Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.
$$<5\over6>$$ обозначим отрезком ОА. Он будет меньше единичного отрезка
$$<7\over15>$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка
$$<18\over4>$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.
$$<25\over7>$$ обозначим отрезком ОD, который будет расположен между 3 и 4.
Разложим 6 и 15 на простые числа и найдем НОК.
Значит:
$<5\over6>><7\over15>$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.
Что мы узнали?
Мы разобрались, что такое отрезок в математике, выделили отличие от луча и прямой. Определили возможность применения его в геометрии для построения треугольников по значениям сторон и в математике для сравнения ряда дробей.
Что такое отрезок в математике? (тема математики, 5 класс)
Отрезок – это часть прямой. В математике тема отрезков имеет большое значение: из них составляют фигуры, с помощью отрезков чертятся рисунки к задачам и сравниваются числа. Поговорим о отрезках и способах их использования в математике 5 класса.
Определение
Отрезок – это часть прямой, ограниченный двумя точками. Это значит, что в отличие от прямой или луча, отрезок конечен и не имеет направления. Числовой отрезок на числовом луче или числовой прямой означает конкретное число. С помощью числовых отрезков можно выполнять сравнение чисел.
Рис. 1. Отрезок, прямая и луч.
Числовой луч обычно принимается для сравнения положительных чисел. Если среди ряда чисел, которые необходимо сравнить, есть отрицательные значения – правильнее будет воспользоваться числовой прямой.
Отрезок всегда имеет определенное значение. Прямую или луч нельзя определить конечным числом в метрах или сантиметрах, поэтому во всех современных подсчетах, как теоретических, так и практических, используются отрезки.
Задача на построение
Построим треугольник со сторонами 3, 5 и 4. Каждая из сторон это отрезок заданной величины. Это еще одно из свойств отрезков. По трем отрезкам заданной величины всегда можно построить треугольник.
Для начала проведем отрезок АВ=3. Можно выбрать и любую другую величину из заданных.
Конкретно в этой задаче такой подбор чисел выполнен для возможности дальнейшей проверки.
Примем точку А за центр окружности с радиусом 4 и проведем ее. Затем примем точку В за центр окружности с радиусом 5. В точке пересечения двух окружностей мы получим точку С – третью точку треугольника.
Треугольник со сторонами 3, 4 и 5 – это классический прямоугольный треугольник. Соответственно с катетами 3, 4 и гипотенузой 5. Эти пропорции были выведены еще в Древней Греции и сегодня очень часто применяются в простых задачах на решение прямоугольных треугольников.
Рис. 2. Построение треугольника.
Конкретно в нашем случае это означает, что получившийся треугольник должен быть прямоугольным по теореме, обратной теореме Пифагора.
25=25 – все верно, условие выполняется. И на рисунке визуально понятно, что треугольник построен правильно. В случае построения произвольного треугольника по трем заданным отрезкам, убедитесь заранее, что выполняются условия неравенства в треугольнике: сторона всегда меньше суммы двух других сторон.
Задача с числовым лучом
Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.
$$<5over6>$$ обозначим отрезком ОА. Он будет меньше единичного отрезка
$$<7over15>$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка
$$<18over4>$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.
$$<25over7>$$ обозначим отрезком ОD, который будет расположен между 3 и 4.
Разложим 6 и 15 на простые числа и найдем НОК.
Значит:
$<5over6>><7over15>$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.
Рис. 3. Числовой луч.
Что мы узнали?
Мы разобрались, что такое отрезок в математике, выделили отличие от луча и прямой. Определили возможность применения его в геометрии для построения треугольников по значениям сторон и в математике для сравнения ряда дробей.
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.