Что такое отрицательное множество
Неотрицательное число
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
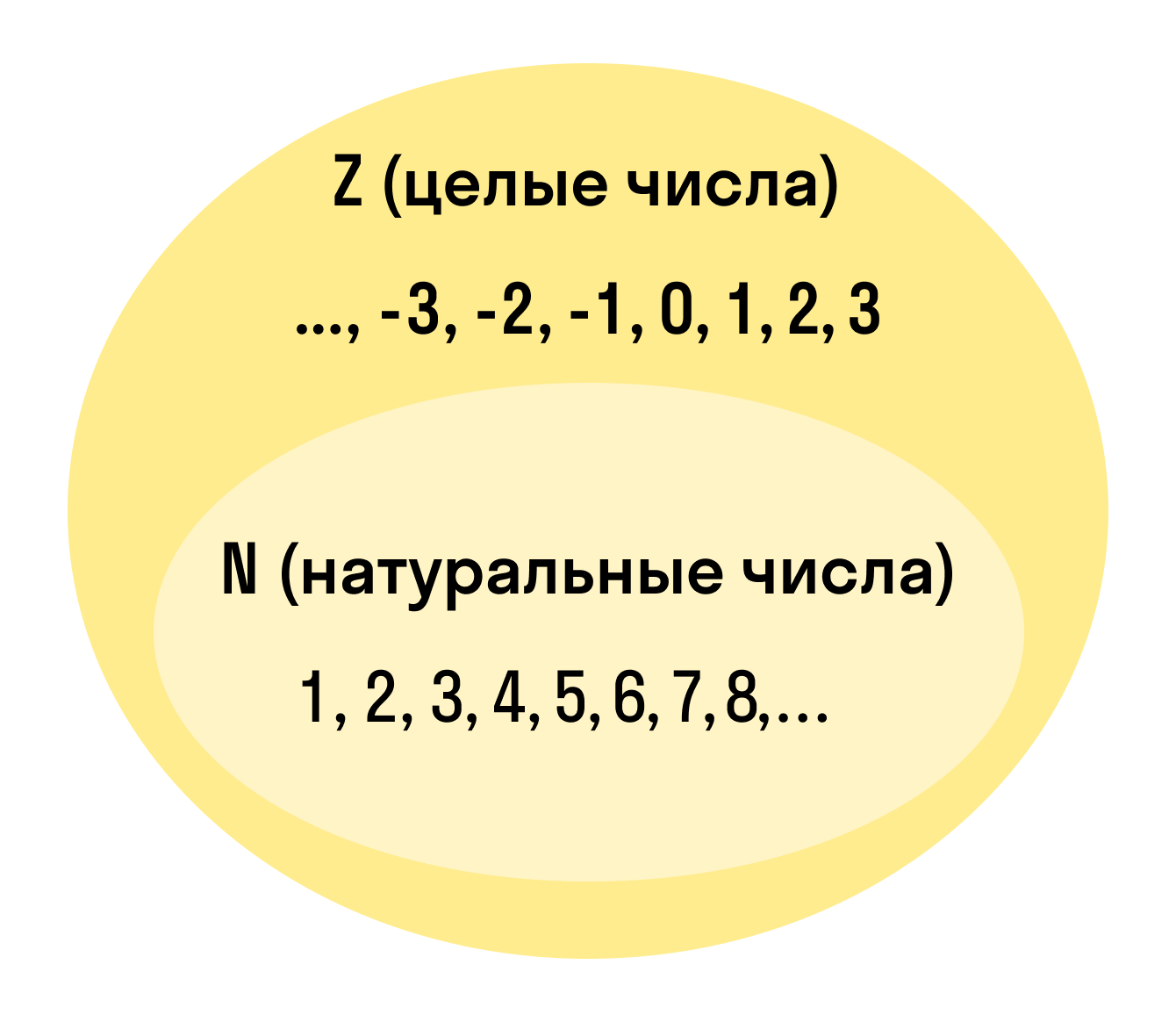
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Множество и его элементы. Подмножества
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество букв слова «математика»:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
D =
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Множество людей является подмножеством приматов, живущих на Земле.
Множество квадратов является подмножеством прямоугольников.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Отрицательные числа
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Множества чисел. Законы действий над различными числами
Множество натуральных чисел
Это бесконечное множество, оно имеет наименьший элемент 1 и не имеет наибольшего элемента. Иногда к натуральным числам добавляют 0, тогда он будет наименьшим элементом.
Законы сложения натуральных чисел
Законы умножения натуральных чисел
Результатом сложения или умножения двух натуральных чисел всегда является натуральное число. Или, говоря иначе, эти операции можно выполнить, оставаясь во множестве натуральных чисел. Относительно вычитания и деления этого сказать нельзя: так, из числа 3 нельзя, оставаясь во множестве натуральных чисел, вычесть число 7; число 15 нельзя разделить на 4 нацело.
Признаки делимости натуральных чисел
Делимость суммы. Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.
Делимость произведения. Если в произведении хотя бы один из сомножителей делится нацело на некоторое число, то и произведение делится на это число.
Эти условия, как для суммы, так и для произведения, являются достаточными, но не необходимыми. Например, произведение 12*18 делится на 36, хотя ни 12, ни 18 на 36 не делятся.
Признак делимости на 2. Для того, чтобы натуральное число делилось на 2, необходимо и достаточно, чтобы его последняя цифра была чётной.
Признак делимости на 5. Для того, чтобы натуральное число делилось на 5, необходимо и достаточно, чтобы его последняя цифра была либо 0, либо 5.
Признак делимости на 10. Для того, чтобы натуральное число делилось на 10, необходимо и достаточно, чтобы цифра единиц была 0.
Признак делимости на 4. Для того, чтобы натуральное число, содержащее не менее трёх цифр, делилось на 4, необходимо и достаточно, чтобы последние цифры были 00, 04, 08 или двузначное число, образованное последними двумя цифрами данного числа, делилось на 4.
Признак делимости на 2 (на 9). Для того, чтобы натуральное число делилось на 3 (на 9), необходимо и достаточно, чтобы сумма его цифр делилась на 3 (на 9).
Множество целых чисел
Числа, противоположные натуральным, образуют множество чисел N’:
Если объединить множества N, N’ и одноэлементное множество , то получим множество Z всех целых чисел:
Для целых чисел верны все перечисленные выше законы сложения и умножения, которые верны для натуральных чисел. Кроме того, добавляются следующие законы вычитания:
Множество рациональных чисел
Чтобы сделать выполнимой операцию деления целых чисел на любое число, не равное нулю, вводятся дроби:
Если к множеству целых чисел присоединить множество всех положительных и отрицательных дробей, то получается множество рациональных чисел Q:

Законы арифметических действий над рациональными числами
Основное свойство дроби. Если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной:

Это свойство используется при сокращении дробей.
Сложение дробей. Сложение обыкновенных дробей определяется следующим образом:

То есть, для сложения дробей с разными знаменателями дроби приводятся к общему знаменателю. На практике при сложении (вычитании) дробей с разными знаменателями дроби приводятся к наименьшему общему знаменателю. Например, так:

Для сложения дробей с одинаковыми числителями достаточно сложить числители, а знаменатель оставить прежним.
Умножение дробей. Умножение обыкновенных дробей определяется следующим образом:

То есть, для умножения дроби на дробь нужно числитель первой дроби умножить на числитель второй дроби и записать произведение в числитель новой дроби, а знаменатель первой дроби умножить на знаменатель второй дроби и записать произведение в знаменатель новой дроби.
Деление дробей. Деление обыкновенных дробей определяется следующим образом:

То есть, для деления дроби на дробь нужно числитель первой дроби умножить на знаменатель второй дроби и произведение записать в числитель новой дроби, а знаменатель первой дроби умножить на числитель второй дроби и произведение записать в знаменатель новой дроби.
Возведение дроби в степень с натуральным показателем. Эта операция определяется следующим образом:

То есть, для возведения дроби в степень числитель возводится в эту степень и знаменатель возводится в эту степень.
Периодические десятичные дроби
Теорема. Любое рациональное число можно представить в виде конечной или бесконечной периодической дроби.

Последовательно повторяющаяся группа цифр после запятой в десятичной записи числа называется периодом, а конечная или бесконечная десятичная дробь, имеющая такой период в своей записи, называется периодической.
При этом любую конечную десятичную дробь считают бесконечной периодической дробью с нулём в периоде, например:
Множество действительных чисел
На числовой прямой, которую мы рассмотрели в связи с множеством целых чисел, могут быть точки, не имеющие координат в виде рационального числа. Так, не существует рационального числа, квадрат которого равен 2. Следовательно, число 




Никакое иррациональное число не может быть представлено в виде периодической дроби. Их представляют в виде непериодических дробей.
Аксиомы о действиях над действительными числами
Аксиомы сложения. Для любых a, b, c из множества R действительных чисел справедливы следующие свойства:
Аксиомы умножения. Для любых a, b, c из множества R действительных чисел справедливы следующие свойства:
Множество комплексных чисел
Комплексные числа вводятся в связи с тем, что действительных чисел недостаточно, чтобы решить любое квадратное уравнение с действительными коэффициентами. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть
Комплексные числа и операции над ними обладают таким количеством замечательных свойств, что они рассмотрены в отдельных материалах нашего сайта: