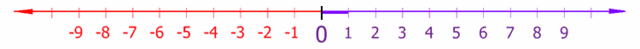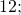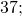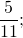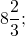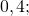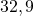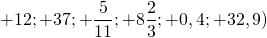Что такое отрицательные числа
Отрицательные числа
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Отрицательные числа
Всего получено оценок: 178.
Всего получено оценок: 178.
Отрицательные числа тяжело воспринимаются учениками 6 класса математики, поскольку долгое время их учат том, что все результаты вычислений, которые меньше нуля неверны. Приходится переучиваться, привыкать к новым правилам. Но на самом деле, если разобраться в отрицательных числах, ничего сложного в них нет.
Отрицательные числа
Отрицательным числом называется любое число меньше нуля. Чтобы обозначить, что число меньше нуля, перед ним ставится знак минус.
Среди отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Практически все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Так же важно помнить, что число 0 не относится ни к положительным, ни к отрицательным числам.
Числовая прямая
Числовая прямая это прямая, которая имеет обозначение 0 и единичных отрезков. На числовой прямой все отрицательные числа лежат левее нуля.
Числовую прямую очень удобно использовать для сравнения отрицательных чисел. Чем ближе отрицательное число на числовой прямой к нулю, тем большим значением оно является.
Правило знаков
Умножение и деление отрицательных чисел происходит согласно правилу знаков:
Сложение отрицательных чисел
При сложении отрицательных чисел действует все то же правило знаков, только в несколько ином виде. Общая формулировка правила знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». Тогда если к одному отрицательному числу прибавить другое, то получится:
-а+(-в)=-а-в – то есть из отрицательного числа вычитается положительное.
Так же работает правило при примерах на вычитание отрицательных чисел:
-а-(-в)=-а+в – к отрицательному числу в итоге прибавляется положительное.
Что мы узнали?
Мы поговорили об отрицательных числах. Рассказали, как удобнее сравнивать отрицательные целые числа, а также как правильно подобные числа перемножать между собой, делить, складывать и вычитать.
Положительные и отрицательные числа: определение, примеры
В этом материале мы объясним, что такое положительные и отрицательные числа. После того, как будут сформулированы определения, мы покажем на примерах, что это такое, и раскроем основной смысл этих понятий.
Что такое положительные и отрицательные числа
Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.
Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.
Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).
Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.
Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.
Мы всегда записываем отрицательные числа с минусом.
В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.
Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.
Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.
Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.
Основной смысл положительных и отрицательных чисел
Мы уже дали основные определения, но для того, чтобы делать верные подсчеты, необходимо понять сам смысл положительности или отрицательности числа. Попробуем помочь вам это сделать.
Отрицательное число
Отрица́тельное число́ — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:
Оба числа называются противоположными друг для друга. Вычитание целого числа a из другого целого числа b равносильно сложению b с противоположным для a:
При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком:
.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же алгебраическим правилам, что и натуральные, но имеют некоторые особенности.
Вариации и обобщения
Понятия положительных и отрицательных чисел можно определить в любом упорядоченном кольце. Чаще всего эти понятия относятся к одной из следующих числовых систем:
Приведенные выше свойства 1-3 имеют место и в общем случае. К комплексным числам понятия «положительный» и «отрицательный» неприменимы.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения. Умножение и деление для отрицательных чисел тогда ещё не были определены. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными.
В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Даже в XVII веке Паскаль считал, что 
, так как ничто не может быть меньше, чем ничто. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Что такое положительное число
В этом материале мы объясним, что такое положительные и отрицательные числа. После того, как будут сформулированы определения, мы покажем на примерах, что это такое, и раскроем основной смысл этих понятий.
Что такое положительные и отрицательные числа
Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.
Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.
Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).
Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.
Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.
Мы всегда записываем отрицательные числа с минусом.
Можно ли сразу сказать, что значение числового выражения log 3 4 – 5 является отрицательным числом? Ответ неочевиден. Нам придется выразить это значение десятичной дробью и потом посмотреть (подробнее см. в материале о сравнении действительных чисел).
В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.
Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.
Есть также определения, основанные на положении данного числа относительно нуля (вспомним, что на правой стороне координатной прямой расположены большие числа, а на левой – меньшие).
Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.
Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.
Отдельно остановимся на том, как правильно читать записи положительных и отрицательных чисел, хотя, как правило, с этим не возникает особых проблем. Для отрицательных чисел мы всегда озвучиваем минус, т.е. – 1 2 5 – это «минус одна целая две пятых».
В случае положительных чисел мы озвучиваем плюс только тогда, когда он явно указан в записи, т.е. + 7 – это «плюс семь». Названия математических знаков неправильно склонять по падежам. Например, верно будет прочесть фразу a = – 5 как « а равно минус пяти», а не «минусу пяти».
Основной смысл положительных и отрицательных чисел
Мы уже дали основные определения, но для того, чтобы делать верные подсчеты, необходимо понять сам смысл положительности или отрицательности числа. Попробуем помочь вам это сделать.
Положительные числа — это числа со знаком «+» перед ними. Знак «+» обычно не пишется (если перед числом не написан знак, то, по умолчанию, это число со знаком «+»).
— положительные числа. Перед этими числами не записан знак, значит, по умолчанию, перед ними стоит знак «плюс» (это сокращенная форма записи
Таким образом, +12=12, то есть +12 и 12 — это одно и то же число, только по-разному обозначенное.
Любое положительное число больше нуля.
0]» title=»Rendered by QuickLaTeX.com»/>
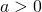
означает, что число a — положительное.
Все натуральные числа являются положительными.
На координатной прямой все положительные числа расположены правее нуля.
Любое положительное число на координатной прямой лежит правее любого отрицательного числа.
Число нуль не является ни положительным, ни отрицательным. Оно отделяет положительные числа от отрицательных.
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).