Что такое палиндромы в геометрии
Исследовательская работа ученицы 10 класса Калошиной Юлии на тему :»Палиндромы в математике»
Название работы: Палиндромы в математике
Автор работы: Калошина Юлия Сергеевна
Место выполнения работы: РК, Яшалтинский р-н, с. Яшалта,
МБОУ «Яшалтинская СОШ имени В. А. Панченко»
Глава 1. Понятие палиндрома в математике _______________________ 5
Глава 2. Формулы палиндромы ________________________________ 11
Глава 3. Именные палиндромы _________________________________ 13
Глава 4. Числовой конструктор _________________________________ 14
Глава 5. Палиндромы в других науках ____________________________ 15
Глава 6. Решение олимпиадных задач и задач ЕГЭ____________ ____ 17
Заключение __________________________________________________ 25
Список литературы ____________________________________________ 26
Обоснование выбора темы: Математика – один из моих любимых предметов, решение различных математических задач привлекало меня, начиная с начальных классов. Именно на уроках математики, при выполнении задач из сборника для подготовки к ЕГЭ, я встретила слово «палиндром». Мне стало интересно, что же это такое? Оказалось, это слово используется в разных науках и имеет множество значений. Я обратила внимание на то, что палиндромы есть как в русском языке, так и в математике. Удивилась: такие разные предметы, а слово одно используют. Но слово-то одно, а вот значения у него разные. Для начала нужно было узнать происхождение слова. Вот что я нашла в толковом словаре:
— Палиндром (греч. «бегущий обратно»), перевертень, «рачья песня» — последовательность звуков или букв, которые и в прямом, и в обратном порядке читаются одинаково: «оно», «я иду, судия». Палиндромом также называется и стих, который при прочтении слева направо или справа налево, дает те же слова. Другое, более точное и распространённое название таких фраз — зеркальные анаграммы. В математике и прочих науках встречаются числа, формулы — палиндромы.
Цели и задачи исследования:
1. Изучить литературу по теме исследования, анализ полученной информации;
2. Изучить свойства чисел- палиндромов;
3. Изучить формулы получения палиндромов при выполнении арифметических операций;
4. Рассмотреть палиндромы в других науках.
5. Создать сборник для подготовки к математическим олимпиадам и ЕГЭ.
Новизна исследования: написание программы на языке программирования Pascal для решения некоторых олимпиадных задач по теме «Палиндромы».
Практическая значимость : созданный мной сборник может использоваться учителями и учениками при подготовке к ЕГЭ; также окажется как нельзя, кстати, при решении задач выходящих за рамки школьной программы, олимпиадных заданий. А работа в целом будет способствовать повышению интереса к изучению математики у учеников и родителей.
Методы исследования: анкетирование; анализ литературы; синтез; сравнение; аналогия.
Гипотеза: После проведения опроса среди одноклассников, я задумалась об актуальности этой темы, ведь задачи по теме «Палиндромы», которых много в ЕГЭ и на олимпиадах, предполагают наличие определенных знаний у учеников; поэтому мне бы хотелось самой узнать как можно больше по этой теме и поделиться этими с другими. Я уверена, что если школьникам изучающим математику углубленно интересен и доступен материал по теме «Палиндромы», то и для нас это должно быть точно так же. Я предполагаю, что элементы высшей математики могут быть доступны и интересны ученикам средней школы. А также, исследуя множество натуральных чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
Объект исследования : множество натуральных чисел
Предмет исследования: числа-палиндромы
Глава 1. Понятие палиндрома в математике
В математике существуют такие числа, которые образуют интересную подгруппу натуральных чисел. Их называют палиндромами. Они обладают необычной историей и имеют свои особенности, интересные свойства.
Говоря о том, что такое палиндром, следует сказать, что известны «перевертыши» с самой глубокой древности. Зачастую им придавался магический сакральный смысл. Появились палиндромы, примеры которых можно встретить в самых разных языках, предположительно в средние века. Древнейший известный палиндром — фраза на латыни, датирующаяся 4 веком н. э.: «SatorArepotenetoperarotas», переводящаяся как «Сеятель Арепо с трудом держит колёса». Фраза обычно записывается в квадрате 5×5, где обнаруживается ещё одно свойство симметрии — её можно читать как по горизонтали, так и по вертикали.
Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Математики связывают с ними множество любопытных фактов и закономерностей: так, палиндромы делятся на пары и семейства, образуют числовые квадраты и целые симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
В математике палиндромом называется строка a1a2…an, для которой выполняются равенства a1=an, a2=an-1, …, a[n-2]=an+1-[n-2], где a1, a2, …, an — некоторые символы. В частности, палиндромами являются все строки из одного символа, а также пустая строка (строка из 0 символов). При этом не обязательно, чтобы строка была осмысленным словом или выражением. С другой стороны, расстановка пробелов в математическом палиндроме тоже должна быть симметричной. Также палиндромам в математике посвящены некоторые теоремы. Вот одна из них:
Теорема : Самой длинной палиндромной подстрокой строки s1s2…sn является самая длинная общая подстрока строк s1s2…sn и sn…s2s1. Если таких общих подстрок несколько, то все они являются палиндромами. (Подстрокой строки S называется строка, полученная из S вычёркиванием некоторых символов без перестановки оставшихся.)
Например, палиндромом является квадрат числа состоящего из единиц 1^2=1 11^2=121 111^2=12321 1111^2=1234321 11111^2=123454321 1*n+1=палиндром
Назовем исходное число и число с переставленными в обратном порядке цифрами взаимно обратными. Выяснено, что сложение некоторых взаимно обратных чисел приводит к образованию числа-палиндрома. Но для многих взаимно обратных чисел такое число палиндром при сложении не образуется. А что будет, если в этом случае сложить результат сложения с его взаимно обратным числом?
Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:
Обратимся к числам простым. В их бесконечном множестве имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11.
С такими числами связано немало интересных закономерностей:
Существует единственный простой палиндром с чётным числом цифр – 11.
1.Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары.
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97.
2. Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.
Аналогичная картина наблюдается у больших простых чисел.
Например: 94849 и 94949; 1177711 и 1178711.
3. Все однозначные числа являются палиндромами.
4. 26 – наименьшее число, не являющееся палиндромом, квадрат которого палиндром. Например: 26² = 676
Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант
5903 раза 5903 раза
А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).
Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:
Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.
Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?
А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1 + 1 + 3) 2 = 1 + 2 + 7 + 6 + 9. Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др.
Глава 2.Формулы – палиндромы.
Под формулами – палиндромами, понимают, выражение (состоящее из суммы или разности чисел), результат которого не меняется в результате прочтения выражения справа налево.
Если сложить числа – палиндромы, то сумма не меняется.
В общем виде это можно записать так:
(100х + 10х+ x ) + (100у + 10 y + у) = (100у + 10 y + у) + (100х + 10 x + х)
100х + 10х+ x + 100у + 10у + y = 100у + 10у + y + 100 x +10х + х
111х + 111у = 111у + 111х
От перестановки слагаемых сумма не изменяется (переместительное свойство сложения).
Задача 1. Найти все пары таких двузначных чисел, чтобы результат их сложения не менялся в результате прочтения суммы справа налево, то есть
Например, 42 + 35 = 53 + 24.
Любое двузначное число можно представить в виде суммы разрядных слагаемых:
Примеры: 41-32 = 23-14, 62-17 = 71-26
Примеры: 39*31=13*93, 42*12=21*24
х1у1/х2у2 =у2х2/у1х1, тогда имеем
х1*у2=х2*у1, т.е.произведение первой цифры первого числа на вторую цифру второго числа равно произведению двух других их цифр.
Глава 3. Именные палиндромы.
Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: число Фибоначчи, число Смита, Репдиджит, Репьюнит.
Числами Фибоначчи называют элементы числовой последовательности. В ней каждое следующее число в ряду получается суммированием двух предыдущих чисел.
Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.
Репдиджит — натуральное число, в записи которого все цифры одинаковые.
Например, 4444, 5555555 и т.д.
Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строк
Например, числа (121,15101051 и т.д.)
Глава 4. Числовой конструктор.
Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.

Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).

Глава 5. Палиндромы в других науках.
Рассмотрим палиндромы в других науках:
1. В изобразительном искусстве:
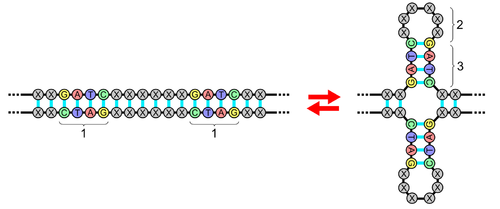
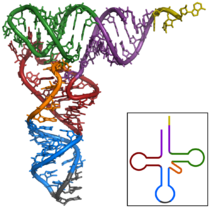
Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.
— Лилипут сома на мосту пилил.
— Нажал кабан на баклажан.
На это дама скромно может ответить «перевертышем»: «Eve» (Ева).
Бывают симметричными не только предложения или наборы букв:
Race fast, safe car (Гони быстро, безопасная машина)
Never odd or even (Никогда нечётные или чётные)
Палиндромные музыкальные произведения играются «как обычно», в соответствии с правилами. После завершения пьесы ноты переворачиваются. Затем произведение играют снова, но мелодия при этом не будет меняться. Итераций может присутствовать сколько угодно, неизвестно при этом, что является низом, а что – верхом. Данные музыкальные произведения можно сыграть вдвоем, при этом читая ноты с обеих сторон одновременно. В качестве примеров таких палиндромических произведений можно привести «Путь мира», написанный Мошелесом, и «Застольную мелодию для двоих», сочиненную Моцартом.
Глава 6. Решение олимпиадных задач и задач ЕГЭ.
А) Приведите пример числа – палиндрома, которое делится на 55. Б) Сколько существует пятизначных чисел – палиндромов, делящихся на 55? в) Найдите 13-е по величине число – палиндром, которое делится на 55.
Б)Теперь займемся пятизначными числами. Ищем число вида 5хух5, которое делится на 55. Попробуем воспользоваться признаками делимости. Число 55=5*11. Поэтому искомые числа должны делиться на 11. «Число делится на11, если сумма цифр, стоящих на нечетных местах равняется сумме цифр, стоящих на четных местах или отличается от нее на11».
Имеем: 5+у+5=х+х или 5+у+5=х+х+11. Получим:
10+у=2х – решением этого уравнения являются пары чисел: (5;0), (6, 2), (7, 4), (8, 6), (9, 8).
10+у=2х+11 – решением этого уравнения являются пары чисел (0,1), (1,3), (2,5), (3,7), (4,9).
Получим 10 чисел – палиндромов:
Таким образом, среди пятизначных чисел ровно 10 палиндромов.
В)назовите 13 –е по счету число-палиндром, которое делится на 55.
Если ряд палиндромов начать с числа 55, то тринадцатым будет 51315.
55, 5005, 5115,5225,5335,5445,5555,5665,5775,5885,5995. 50105. 51315, 52525,53735,54945,55055,56265,57475,58685,59895
а) Приведите пример числа-палиндрома, который делится на 15. б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15? в) Найдите 37-е по величине число-палиндром, которое делится на 15.
1)При Z =0 получается 5 y 0 y 5
2)При Z =1 получается 5+ y +1+ y +5=11+2 y
При y =1 51015 При y =2 52125
При y =454045 При y =5 55155
При y =7 57075 При y =858185
3) При Z =2 получается 12+2 y /3 4) При Z =3 получается 13+2 y /3
При y =0 50205 При y =1 51315
При y =353235 При y =4 54345
При y =656265 При y =7 57375
Таким образом, заметим повторение.
Для набора y =(1,4,7)= z =0,3,6,9 (12 чисел)
Для набора y =(2,5,8) )= z =1,4,7 (9 чисел)
Для набора y =(0,3,6,9)= z =2,5,8( 12 чисел)
В)Найдем 37-е по счету число палиндром
1)При двузначных нет палиндромов/15
2)Среди 3-значных 5 y 5 y =2,5,8 525,555,585
4)Среди 5-значных выписываем все числа
5)Упорядочиваем все числа и находим 37 –е число по счету
Ответы: а) 5115; б) 33; в) 59295
Решение : аналогично предыдущей задаче.
Ответ :а)585; б)11 ;в)56565
Задача 4. Автомобилист посмотрел на счетчик своего автомобиля и увидел симметричное число (палиндром) 15951 км (читается одинаково слева направо или наоборот). Он подумал, что, скорее всего, уже не скоро появится другое симметричное число. Однако уже через 2 часа он обнаружил новое симметричное число. С какой постоянной скоростью автомобилист проехал эти два часа?
Сколько существует 5-значных палиндромов, делящихся на 9.
Задача 6: . Представьте число 2015 в виде суммы двух палиндромов.
Решение: 2015=1551+464. Догадаться нетрудно. Самый большой трехзначный палиндром это 999. Но 999+999=1998
Если дату 10 февраля 2001 года записать в виде 10.02.2001, а затем убрать точки, то получится палиндром (т.е. число, читающееся слева направо и справа налево одинаково). Найдите ближайшую к 10.02.2001 дату, обладающую тем же свойством. Решение: Рассмотрим два случая:
1) требуемая дата еще не наступила,
2) требуемая дата уже прошла.
Итак, 1) в 2001 году других палиндромов быть не может, а в следующем (2002) году это должен быть 20 день второго месяца.
Ответ. 1) 20 февраля 2002 2) 29 ноября 1192 года.
а) двузначных ; б) трехзначных ; в) четырехзначных ; г) пятизначных
На 2 делится любое четное число. Поэтому,
Задача 9:
б) трехзначных ; в) четырехзначных ; г) пятизначных
Решение: На 3 число делится, если сумма его цифр делится на 3.
а) среди двухзначных таких чисел 3: 33, 66 и 99.
Палиндром
Существуют разновидности, когда чтение производится не в обратном направлении, а в прямом, но с другого места в «размноженном» термине, например, кабанкабан, кольцокольцо, викивики. Такие «разночтения» могут встречаться и в ДНК.
Содержание
Примеры палиндромов
Русский язык: А роза упала на лапу Азора. (А. Фет)
Аргентина манит негра
Английский язык: «Madam, I’m Adam» («Мадам, я — Адам», — представился первый человек первой женщине)
«Eve» («Ева», — скромно ответила она)
Латинский язык: Sum summus mus (Я — сильнейшая мышь)
Финский язык: Saippuakivikauppias (самое длиннное в мире слово-палиндром) [5]
Математика
Известные русские палиндромисты
В биологии
В структуре нуклеиновых кислот имеются относительно короткие взаимно комплементарные участки, имеющие «зеркальные» последовательности нуклеотидов, которые могут образовывать дуплексы. Общее число таких «перевертышей» в геноме человека оценено от 100 тыс. до 1 млн. При этом они относительно равномерно распределены по ДНК. [источник не указан 1092 дня] Палиндромы способны обеспечить увеличение объёма информации без увеличения числа нуклеотидов.
Важную роль играют палиндромные последовательности в формировании некоторых типов нуклеиновых кислот, например, в случае транспортных РНК (см. рис).
В музыке
Пьесу играют как обычно, но после того как она заканчивается, ноты переворачивают произведение играют заново, причем мелодия не изменится. Таких итераций может быть сколько угодно и не известно что же является верхом а что низом. Такие произведения можно играть вдвоем читая ноты с разных сторон. Примерами музыкальных палиндромов могут являться произведения «Застольная мелодия для двоих» Моцарта и «Путь Мира» Мошелеса.
См. также
Примечания
Литература
Полезное
Смотреть что такое «Палиндром» в других словарях:
Палиндром — (греч. «бегущий вспять», иначе палиндромон, перевертень) фраза, построенная так, что ее можно читать и справа и слева, сохраняя смысл, напр.: «Я иду с мечем судия», «Атака заката» и т. д. Более сложным видом П. (словесного, а не буквенного)… … Литературная энциклопедия
ПАЛИНДРОМ — (греч., от palin опять, и dromos бег). 1) стих, имеющий при прямом и при обратном чтении одинаковый смысл. Напр. А роза упала на лапу Азора. 2) загадка на слово, которое при прямом чтении имеет одно значение, а при обратном другое. Словарь… … Словарь иностранных слов русского языка
палиндром — а, м. palindrome adj., англ. <гр. бегущий обратно< palin назад + dromos путь. Слово или сочетание слов, читающееся одинаково и с начала и с конца, например кабак, шалаш. БАС 1. Не вермишель лешим ревень, но ракам еще макарон. Пример… … Исторический словарь галлицизмов русского языка
палиндром — палиндромон, перевертыш, перевертень Словарь русских синонимов. палиндром сущ., кол во синонимов: 4 • saippuakivikauppias (1) • … Словарь синонимов
Палиндром — ПАЛИНДРОМ искусственная стихотворная форма, состоящая в том, что слова в стихотворении расположены: 1) или так, что отдельные буквы, располагаясь в обратном порядке, т. е. от конца к началу, дают ту же фразу, какая получается при чтении стиха … Словарь литературных терминов
ПАЛИНДРОМ — то же, что перевертень … Большой Энциклопедический словарь
ПАЛИНДРОМ — и ПАЛИНДРОМОН, палиндромона, муж. (от греч. palindromeo бегу назад) (лит.). Стихотворение или фраза, читающиеся одинаково и с начала и с конца, напр.: я иду с мечем судия (Державин), течет и нежен, нежен и течет (Хлебников). Толковый словарь… … Толковый словарь Ушакова
ПАЛИНДРОМ — и ПАЛИНДРОМОН, палиндромона, муж. (от греч. palindromeo бегу назад) (лит.). Стихотворение или фраза, читающиеся одинаково и с начала и с конца, напр.: я иду с мечем судия (Державин), течет и нежен, нежен и течет (Хлебников). Толковый словарь… … Толковый словарь Ушакова
палиндром — Кодовая последовательность, совпадающая сама с собой при ее чтении в обратном порядке, т.е. с конца. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики … Справочник технического переводчика
Палиндром. Какие бывают палиндромы?
В русском языке довольно много слов-палиндромов. Приводим их группами по количеству букв.
Палиндромы из 1 буквы
Палиндромы из 2 букв
Палиндромы из 3 букв
Палиндромы из 4 букв
Палиндромы из 5 букв
Палиндромы из 6 букв
Палиндромы из 7 букв
Палиндромы из 9 букв

Палиндромы из нескольких слов
В разных языках существует огромное количество палиндромов, состоящих из нескольких слов. Короткие фразы-палиндромы, как правило, изящны и заключают в себе некий смысл.
Море могуче. В тон ему, шумен отвечу Гомером:
Палиндромы на иностранных языках
Древнейший из сохранившихся палиндромов написан на латыни и датируется 4 в. н.э. Это фраза «Sator Arepo tenet opera rotas», что означает «Сеятель Арепо с трудом держит колёса». Обычно записывают ее в форме квадрата:
S A T O R
A R E P O
T E N E T
O P E R A
R O T A S
Еще один изящный палиндром, понятный даже без знания инотсранных языков:
«Madam, I’m Adam» («Мадам, я — Адам», — представился первый человек первой женщине)
«Eve» («Ева», — скромно палиндромом ответила она).
Самые длинные палиндромы в мире
В палиндромичном году (2002) Петер Норвиг (англ. Peter Norvig) закончил пятилетнюю работу с применением компьютера по созданию самого длинного палиндрома на английском языке, состоящего из 17 259 слов. Написанная в традициях классического палиндрома A man, a plan, a canal. Panama («Человек, план, канал — Панама»), эта фраза начинается A man, a plan, a cameo, Zena… и заканчивается …Ibanez, OEM, a canal, Panama. К сожалению, в целом этот длиннейший палиндром лишен смысла.
Самый длинный связный роман-палиндром «Olson in Oslo» был написан Лоуренсом Левиным (англ. Lawrence Levine) и состоит из 31 594 слов. Но он труден для чтения из-за применения странных грамматических структур и архаичного языка.
Еще один очень длинный палиндром был составлен Джеральдом Бернсом (англ. Gerald M. Berns), и представляет собой бессмысленный список из 31 358 слов.