Что такое парадокс зенона
Парадоксы Зенона вводили в недоумение многих ученых и философов до 17 века. И до сих пор многие ученые спорят о бесконечности, структуре пространства и времени, хотя началось все с нескольких парадоксальных утверждений, ставящих поначалу в логический тупик любого умного человека.
История возникновения парадоксов Зенона
Зенон Элейский – философ Древней Эллады, ученик основателя Элейской школы – Парменида. Жил он с 515 по 450 год до нашей эры, о его жизни известно очень мало. Родился в городе Элее в южной части Италии. По утверждению Платона, Зенон побывал в Афинах и встретился с Сократом. Прославился благодаря своим апориям, в виде которых был сформулирован знаменитый парадокс Зенона. Апории Зенона представляют собой парадоксальные рассуждения, само же слово «апория» с греческого языка обозначает «безвыходность».
Парадоксы о движении и времени
Проблема решилась после идеи дифференциального исчисления, которую предложили Ньютон и Лейбниц. Там есть понятие «предел», так прояснилась разница между разбиением времени и разбиением на отрезки определенного пути. К тому же загадка разрешилась, когда ученые научились пользоваться бесконечно малыми величинами. Апории Зенона породили с тех пор множество различных вариаций. Кроме того, возможно, добавились некоторые детали. Мы перечислим сохранившиеся до наших дней парадоксы Зенона и кратко расскажем об их сути. Во всяком случае, попытаемся это сделать.
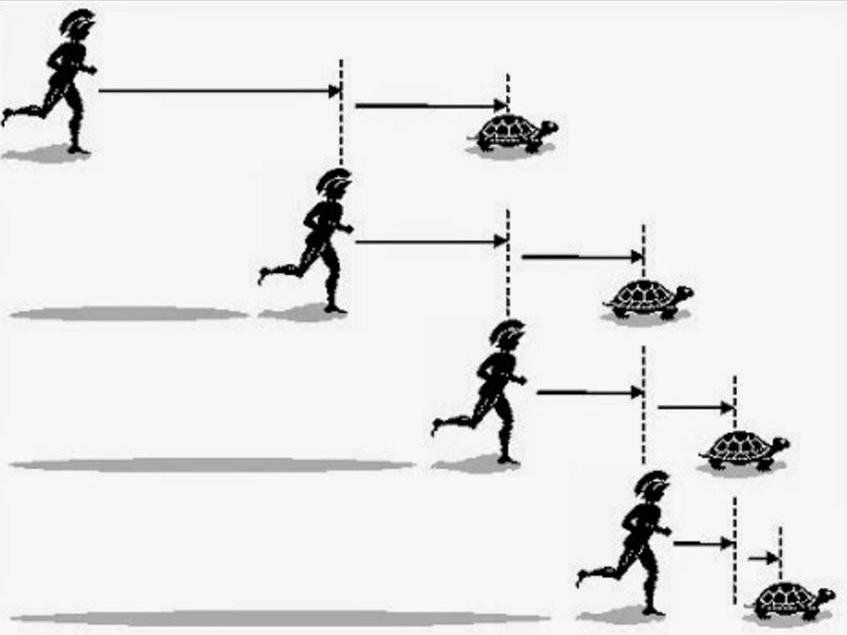
Парадокс Зенона об Ахиллесе и черепахе
Герой мифов Древней Греции Ахиллес соревнуется в скорости бега с черепахой. Условия таковы, что черепаха стартует немного дальше, Ахиллес находится от нее на расстоянии в 1000 шагов.
Чтобы догнать черепаху, Ахиллес должен достигнуть сначала места, с которого черепаха стартовала. Но как только он добежит до этого места, черепаха успеет проползти 100 шагов. Это расстояние, которое она проползла, еще предстоит преодолеть Ахиллесу, но к тому времени она уползет еще дальше на 10 шагов и так далее. Число таких отрезков, которые нужно преодолеть Ахиллесу, по утверждению Зенона, может быть бесконечным, ведь величина этих отрезков все время будет уменьшаться до бесконечно малых величин.
Выходит, если следовать такой логике, древнегреческий герой никогда не догонит черепаху. Парадокс Зенона заключается в существовании бесконечного количества бесконечно малых отрезков, но в реальной жизни бегун наверняка обгонит медлительное животное.
Летящая стрела
Этот парадокс получил название «Стрела». Это еще одна апория, которую Зенон сформулировал приблизительно следующими словами. Если что-либо пребывает в движении, то оно движется либо в том месте, которое оно занимает собой, либо оно движется там, где его нет. Но оно не способно двигаться в том месте, которое оно занимает. Так как в каждую секунду оно занимает полностью все это место. Но и в том месте, где его нет, оно не может двигаться. Следовательно, движение само по себе невозможно.
По утверждению Зенона, стрела, когда летит, одновременно пребывает в покое. Потому что в каждый момент она занимает одно и то же пространство, равное ей. То есть стрела пребывает в покое относительно места, где она находится в определенный промежуток времени. Получается, что летящая стрела неподвижна. Если она неподвижна в определенный момент, значит, она находится в покое и в другие моменты времени. И нет того момента, когда стрела двигалась.
Дихотомия
Парадокс, который будет приведен далее, имеет название «дихотомия». В переводе с греческого языка оно означает «разделение надвое», и дано оно Аристотелем. Эта апория изложена примерно по такому же принципу, как и парадокс Зенона об Ахиллесе и черепахе.
В оригинале говорится о бегуне, который не в состоянии даже стартовать, ведь движения, по мнению Зенона, не существует. Но есть еще и распространенный вариант про пересечение комнаты.
Чтобы пересечь комнату, нужно сначала пересечь половину комнаты. На это уйдет определенная единица времени. После этого останется определенное расстояние, нужно преодолеть половину его за еще одну единицу времени. Затем тот отрезок пути, что остался, нужно разделить еще надвое и пройти половину этого отрезка за то же время. Тогда опять остается определенное расстояние, половину которого надо пересечь. Получается, что комнату пересекать можно бесконечно.
Две колонны на стадионе
Две колонны людей, одинаковые по длине, двигаются параллельно с одинаковой скоростью в противоположных направлениях. По утверждению Зенона, время которое истечет, когда колонны будут проходить мимо друг друга, равно половине того времени, которое нужно одному человеку, чтобы пройти мимо всей колонны.
Разрешение парадоксов Зенона
Из четырех перечисленных апорий наибольшую известность получили первые три. Четвертая появилась из-за неправильного понимания природы относительного движения.
Все апории можно легко опровергнуть экспериментально. Ничего не мешает пересечь комнату, выпустить стрелу и обогнать черепаху.
Рассмотрим парадокс, связанный с пересечением комнаты. Конечно, если разделить расстояние надвое и пройти половину, на это уйдет определенное количество времени. Останется еще расстояние, которое тоже нужно поделить надвое и пройти половину. Но для этого времени понадобится в два раза меньше. Чем меньше становится расстояние, которое необходимо преодолеть, тем больше будет сокращаться время на его прохождение. Выходит, при пересечении комнаты в конце требуется неограниченное число бесконечно маленьких временных отрезков. Но если сложить все отрезки, получится определенное число – оно-то и будет временем, затраченным на пересечение комнаты. Получается, пересечь комнату вполне возможно за определенный промежуток времени. Это доказательство схоже с нахождением предела при дифференциальном исчислении. Древнегреческий философ Зенон ошибочно предполагал, что при прохождении бесконечно малых расстояний каждый раз требуется одно и то же время.
Что касается парадокса Зенона «Летящая стрела», еще Аристотель его раскритиковал, утверждая, что каждый момент времени не может быть неделимым сам по себе. Еще он говорил, что рассуждения Зенона о том, что если все занимающее равное себе место пребывает в покое, и если то, что пребывает в движении, всегда занимает в любой момент такое же место, то стрела неподвижна, ошибочны.
Квантовый эффект
Парадоксы Зенона были опровергнуты со временем многими учеными. Но они все же внесли определенный вклад в науку. В квантовой физике на сегодняшний момент есть такое понятие, как квантовый парадокс Зенона. Он заключается в том, что если наблюдать за нестабильной частицей, например, проводить измерения, проверять, распалась частица или нет, то возникает некоторое замедление радиоактивного распада.
Предполагается, что если непрерывно наблюдать за частицей, то она может вообще не распасться. В 90-х годах прошлого века этот квантовый эффект был подтвержден с помощью ряда экспериментов.
Парадокс Зенона
Зенон (ок. 490 г. До Р. Х. — ок. 430 г. До Р. Х.) принадлежал к элейской греческой философской школе, которая провозглашала, что любое изменение в мире иллюзорно, а бытие едино и неизменно. Учитель Зенона Парменид утверждал: «Вселенная неизменна, ибо, признав изменение, мы признали бы небытие того, что существует, а лишь бытие существует» (http://www.proza.ru/2010/02/20/316). Точка зрения Зенона более диалектична. Он говорил: «Предположите существование вашего изменения; в нем, как в изменении, содержится его ничто, или, иначе говоря, оно не существует». При этом нужно заметить, что для Парменида изменение означало определенное и завершенное движение, а Зенон высказывался и выступал против движения как такового, или, иначе говоря, против чистого движения. «Чистое бытие не есть движение, оно, наоборот, есть ничто движения».
Тем, кто придерживался противоположной точки зрения Зенон предлагал опровергнуть его парадокс, сформулированный в виде четырех апорий (от греч. aporia «безвыходность»), показывающий, что движение (образец «видимого» изменения) логически невозможно. Большинству современных читателей парадокс Зенона знаком именно в приведенной выше формулировке (ее иногда называют дихотомией — от греч. dichotomia «разделение надвое»). Первая апория провозглашала, что невозможно пересечь комнату. Ведь сначала нужно преодолеть половину пути. Но затем нужно преодолеть половину того, что осталось, затем половину того, что осталось после этого, и так далее. Это деление пополам будет продолжаться до бесконечности, из чего делается вывод, что вам никогда не удастся пересечь комнату.
Апория, известная под названием «Ахилл», еще более впечатляюща. Древнегреческий герой Ахилл, непобедимый в беге, собирается состязаться с черепахой. Если черепаха стартует немного раньше Ахилла, то ему, чтобы ее догнать, сначала нужно добежать до места ее старта. Но к тому моменту, как он туда доберется, черепаха проползет некоторое расстояние, которое нужно будет преодолеть Ахиллу, прежде чем догнать черепаху. Но за это время черепаха уползет вперед еще на некоторое расстояние. А поскольку число таких отрезков бесконечно, быстроногий Ахилл никогда не догонит черепаху.
А вот третья апория словами самого Зенона: «Если что-то движется, то оно движется либо в том месте, которое оно занимает, либо в том месте, где его нет. Однако оно не может двигаться в том месте, которое оно занимает (так как в каждый момент времени оно занимает все это место), но оно также не может двигаться и в том месте, где его нет. Следовательно, движение невозможно. Этот парадокс называется «Стрела».
Наконец, существует четвертая апория, в которой речь идет о двух равных по длине колоннах людей, движущихся параллельно с равной скоростью в противоположных направлениях. Зенон утверждает, что время, за которое колонны пройдут друг мимо друга, составляет половину времени, нужного одному человеку, чтобы пройти мимо всей колонны.
Сам Гегель, уделивший парадоксу Зенона важное место в своих «Лекциях по истории философии», строит свои доводы следующим образом. Первая форма опровержения состоит в утверждении: «Движение не обладает истинностью, так как движущееся должно дойти до половины пространства, прежде чем оно дойдет до цели». То есть, мы должны признать, как предпосылку, непрерывность пространства. Движущееся должно достигнуть известного конечного пункта; этот путь представляет собою целое. Чтобы пройти целое, движущееся должно сначала пройти половину; теперь конечным пунктом является конец этой половины, но эта половина пространства есть в свою очередь целое, которое, таким образом, также имеет в себе половины; движущееся, следовательно, прежде должно дойти до половины этой половины – и т.д. до бесконечности. Зенон здесь указывает на бесконечную делимость пространства: так как пространство и время абсолютно непрерывны, то нигде нельзя остановиться с делением. Каждая величина (а каждое время и каждое пространство всегда обладают величиной) делима в свою очередь на две половины, которые должны быть пройдены, и это всегда имеет место, какое бы маленькое пространство мы ни взяли. Движение оказывается прохождением этого бесконечного количества моментов; оно поэтому никогда не кончается; движущееся, следовательно, не может дойти до своего конечного пункта.
Общее разрешение этого противоречия, даваемое Аристотелем, заключается в том, что пространство и время не бесконечно разделены, а лишь бесконечно делимы. Но может показаться и действительно кажется, что, будучи делимы, т.е. разделены в возможности, они должны быть разделены также и в действительности, ибо в противном случае их нельзя было бы делить до бесконечности. Исходя из этого соображения, мы, не задумываясь, соглашаемся, как с чем-то невинным, с утверждением, что движущееся должно дойти до половины; но, таким образом, пишет Гегель, мы уже согласились со всем остальным, т.е. согласились, что оно никогда не дойдет, ибо сказать это раз равнозначно повторению этого высказывания бесчисленное количество раз. Возражают, что в большом пространстве можно признать необходимость дойти до половины, но вместе с тем представляют себе дело так, что в очень маленьком пространстве доходят до такой точки, где деление пополам больше уже невозможно, т.е. доходят до неделимого, не непрерывного, доходят до того, что не есть пространство. Но это неверно, ибо непрерывность есть существенное определение; в предположении наличности половины содержится уже перерыв непрерывности. Следует сказать: не существует половины пространства, ибо пространство непрерывно; можно разломать на две половины кусок дерева, но не пространство, а в движении имеется только пространство. Можно было бы сказать: пространство состоит из бесконечно многих точек. Обыкновенно представляют себе, что можно переходить от одной такой неделимой точки к другой, но таким образом нельзя продвинуться дальше, ибо таких точек – бесчисленное множество. Своим невинным на первый взгляд допущением Зенон заставляет нас расщепить непрерывное на его противоположность, на неопределенное множество, в следствии этого мы не принимаем непрерывности и, следовательно, не принимаем наличности движения. Ошибочно утверждение, будто оно возможно, если дойдешь до одной такой точки, которая уже не непрерывна; это ошибочно, потому что движение есть связь.
Точно также обстоит дело со второй апорией. Более быстрое движение, утверждает Зенон, не помогает Ахиллу пробежать то расстояние, на которое оно отстает; время, которое он употребляет для этого, используется всегда и более медлительным, чтобы в продолжение его снова опередить первое, хотя и на все меньшее и меньшее расстояние, которое, однако, благодаря непрерывному делению пополам, никогда вполне не исчезает. Аристотель, рассматривая этот довод, говорит по поводу его кратко: «Это доказательство представляет ту же самую бесконечную деленность; оно, однако, ложно, ибо быстроходный все же догонит медленного, если будет дозволено преступить границу». Его ответ, пишет Гегель, правилен и содержит в себе все нужное: в этом представлении принимаются именно две точки времени и два пространства, отделенные друг от друга, т.е. отграниченные друг от друга; если же мы, напротив, примем, что время и пространство непрерывны, так что две точки времени или пространства, как непрерывные, соотнесены друг с другом, то они суть две точки и в равной же мере не суть две точки, а тождественны. В представлении мы разрешаем этот вопрос легче всего, говоря: «Так как второе тело быстроходнее, то оно в одно и то же самое время проходит более значительное пространство, чем медленно движущееся; оно, следовательно, может дойти до того места, откуда начинает свое движение первое тело, а затем – пойти еще дальше». Время, значит, и есть то ограниченное, за пределы которого, согласно Аристотелю, мы должны выйти, то, через которое должно проникнуть дальше; так как оно непрерывно, то мы, чтобы разрешить затруднение, должны сказать, что то, чт; мы различаем как две части времени, должно быть взято как одна часть времени. В движении две точки времени, равно как и две точки пространства, суть на самом деле одна точка. Ведь когда мы желаем уяснить себе вообще движение, мы говорим, что тело находится в одном месте, а затем идет в другое место. Во время движения оно уже не находится в первом месте, но вместе с тем еще не находится во втором месте; если бы оно находилось в одном из этих мест, оно находилось бы в покое. Но где же оно находится? Если скажем, что оно находится между этими двумя местами, то этим в действительности ничего не скажем, ибо в таком случае оно также находилось бы в одном месте, и перед нами возникло бы, следовательно, то же самое затруднение. Но двигаться означает быть в данном месте и в то же время не быть в нем, – следовательно, находиться в обоих местах одновременно; в этом состоит непрерывность времени и пространства, которая единственно только и делает возможным движение. Зенон же в своем умозаключении строго отделял друг от друга эти две точки. Дискретность времени и пространства признаем и мы, но в равной же мере им должно быть дозволено преступать границу, т.е. полагать границу как то, что не есть граница, или полагать деленные части времени, которые вместе с тем суть и неделенные части.
Из сказанного очевидно, каким образом можно опровергнуть третью апорию Зенон, когда он говорит: «Летящая стрела находится в покое, и именно потому, что движущееся всегда находится в равном себе «теперь» и равном себе «здесь», в неразличимом»; стрела – здесь и здесь и здесь. Мы можем сказать о стреле, что она всегда одна и та же, так как она всегда находится в одном и том же пространстве и в одном и том же времени; она не выходит за пределы своего пространства, не занимает другого, т.е. большего или меньшего пространства, но это мы называем не движением, а покоем. В «здесь» и «теперь» упразднено становление иным; в них, правда, положена ограниченность вообще, но она положена лишь как момент; так как в «здесь» и «теперь», как таковых, не содержится различия. Аристотель говорит об этом третьем доказательстве: «Оно возникает из того, что Зенон принимает, будто время состоит из теперь, но если мы не согласимся с этим, не получится и вывода».
Что до четвертого возражения Зенона, то оно построено на противоречии, получающемся при движении в противоположных направлениях; общее движение целиком получает одно тело, тогда как само по себе оно проделывает только часть. А на самом деле расстояние, пройденное одним телом, есть сумма расстояний, пройденных обоими.
Парадокс Зенона
Движение невозможно. В частности, невозможно пересечь комнату, так как для этого нужно сначала пересечь половину комнаты, затем половину оставшегося пути, затем половину того, что осталось, затем половину оставшегося.
Зенон Элейский принадлежал к той греческой философской школе, которая учила, что любое изменение в мире иллюзорно, а бытие едино и неизменно. Его парадокс (сформулированный в виде четырех апорий (от греч. aporia «безвыходность»), породивших с тех пор еще примерно сорок различных вариантов) показывает, что движение, образец «видимого» изменения, логически невозможно.
Большинству современных читателей парадокс Зенона знаком именно в приведенной выше формулировке (ее иногда называют дихотомией — от греч. dichotomia «разделение надвое»). Чтобы пересечь комнату, сначала нужно преодолеть половину пути. Но затем нужно преодолеть половину того, что осталось, затем половину того, что осталось после этого, и так далее. Это деление пополам будет продолжаться до бесконечности, из чего делается вывод, что вам никогда не удастся пересечь комнату.
Апория, известная под названием Ахилл, еще более впечатляюща. Древнегреческий герой Ахилл собирается состязаться в беге с черепахой. Если черепаха стартует немного раньше Ахилла, то ему, чтобы ее догнать, сначала нужно добежать до места ее старта. Но к тому моменту, как он туда доберется, черепаха проползет некоторое расстояние, которое нужно будет преодолеть Ахиллу, прежде чем догнать черепаху. Но за это время черепаха уползет вперед еще на некоторое расстояние. А поскольку число таких отрезков бесконечно, быстроногий Ахилл никогда не догонит черепаху.
Вот еще одна апория, словами Зенона:
Если что-то движется, то оно движется либо в том месте, которое оно занимает, либо в том месте, где его нет. Однако оно не может двигаться в том месте, которое оно занимает (так как в каждый момент времени оно занимает все это место), но оно также не может двигаться и в том месте, где его нет. Следовательно, движение невозможно.
Этот парадокс называется стрела (в каждый момент времени летящая стрела занимает место, равное ей по протяженности, следовательно она не движется).
Наконец, существует четвертая апория, в которой речь идет о двух равных по длине колоннах людей, движущихся параллельно с равной скоростью в противоположных направлениях. Зенон утверждает, что время, за которое колонны пройдут друг мимо друга, составляет половину времени, нужного одному человеку, чтобы пройти мимо всей колонны.
Из этих четырех апорий первые три наиболее известны и наиболее парадоксальны. Четвертая просто связана с неправильным пониманием природы относительного движения.
Самый грубый и неизящный способ опровергнуть парадокс Зенона — это встать и пересечь комнату, обогнать черепаху или выпустить стрелу. Но это никак не затронет хода его рассуждений. Вплоть до XVII века мыслители не могли найти ключ к опровержению его хитроумной логики. Проблема была разрешена только после того, как Исаак Ньютон и Готфрид Лейбниц изложили идею дифференциального исчисления, которое оперирует понятием предел; после того как стала понятна разница между разбиением пространства и разбиением времени; наконец, после того как научились обращаться с бесконечными и бесконечно малыми величинами.
Возьмем пример с пересечением комнаты. Действительно, в каждой точке пути вам надо пройти половину оставшегося пути, но только на это вам понадобится в два раза меньше времени. Чем меньший путь осталось пройти, тем меньше времени на это понадобится. Таким образом, вычисляя время, нужное для того, чтобы пересечь комнату, мы складываем бесконечное число бесконечно малых интервалов. Однако сумма всех этих интервалов не бесконечна (иначе пересечь комнату было бы невозможно), а равна некоторому конечному числу — и поэтому мы можем пересечь комнату за конечное время.
Такой ход доказательства аналогичен нахождению предела в дифференциальном исчислении. Попробуем объяснить идею предела в терминах парадокса Зенона. Если мы разделим расстояние, которое мы прошли, пересекая комнату, на время, которое мы на это потратили, мы получим среднюю скорость прохождения этого интервала. Но хотя и расстояние, и время уменьшаются (и в конечном счете стремятся к нулю), их отношение может быть конечным — собственно, это и есть скорость вашего движения. Когда и расстояние, и время стремятся к нулю, это отношение называется пределом скорости. В своем парадоксе Зенон ошибочно исходит из того, что, когда расстояние стремится к нулю, время остается прежним.
Но мое любимое опровержение парадокса Зенона связано не с дифференциальным исчислением Ньютона, а с цитатой из скетча «Второго города», комедийного театра в моем родном Чикаго. В этом скетче лектор описывает различные философские проблемы. Дойдя до парадокса об Ахилле и черепахе, он произносит следующее:
Но это же просто смешно. Каждый сидящий в этой комнате может выиграть гонку с черепахой. Даже такой старый и степенный философ, как Бертран Рассел, — даже он может обогнать черепаху. Но если он и не сможет победить ее, он сможет ее перехитрить!
По-моему, неплохой итог для всего сказанного выше.
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Отправляясь куда бы то ни было, необходимо пройти сначала половину пути, затем половину оставшегося расстояния, и так до бесконечности. Отсюда неминуемо следует вывод: достичь конечного пункта в принципе невозможно, а стало быть, невозможно и само движение
Этот парадокс носит название парадокса дихотомии. Авторство приписывается древнегреческому философу Зенону. Предполагается, что он был сформулирован в качестве доказательства единичности вселенной, и того, что изменение, в том числе и движение – невозможно (как полагал учитель Зенона Парменид).
Люди интуитивно отвергали этот парадокс на протяжении многих веков. С математической точки зрения, решение, сформулированное в XIXвеке, состоит в том, чтобы признать, что половина плюс одна четвертая плюс одна восьмая плюс одна шестнадцатая и т.д. составляет единицу. Это все равно, что сказать: ноль целых и девять в периоде равно единице.
Однако, это теоретическое решение фактически не дает ответа на вопрос, как объект может достичь конечной точки своего движения. Решение этой задачи является более сложным и до сих пор не вполне понятным, если опираться на теории XX столетия, которые отрицают бесконечную делимость материи, времени и пространства.
Зенон Элейский принадлежал к той греческой философской школе, которая учила, что любое изменение в мире иллюзорно, а бытие едино и неизменно. Его парадокс (сформулированный в виде четырех апорий (от греч. aporia «безвыходность»), породивших с тех пор еще примерно сорок различных вариантов) показывает, что движение, образец «видимого» изменения, логически невозможно.
Большинству современных читателей парадокс Зенона знаком именно в приведенной выше формулировке (ее иногда называют дихотомией — от греч. dichotomia «разделение надвое»). Чтобы пересечь комнату, сначала нужно преодолеть половину пути. Но затем нужно преодолеть половину того, что осталось, затем половину того, что осталось после этого, и так далее. Это деление пополам будет продолжаться до бесконечности, из чего делается вывод, что вам никогда не удастся пересечь комнату.
Апория, известная под названием Ахилл, еще более впечатляюща. Древнегреческий герой Ахилл собирается состязаться в беге с черепахой. Если черепаха стартует немного раньше Ахилла, то ему, чтобы ее догнать, сначала нужно добежать до места ее старта. Но к тому моменту, как он туда доберется, черепаха проползет некоторое расстояние, которое нужно будет преодолеть Ахиллу, прежде чем догнать черепаху. Но за это время черепаха уползет вперед еще на некоторое расстояние. А поскольку число таких отрезков бесконечно, быстроногий Ахилл никогда не догонит черепаху.
Вот еще одна апория, словами Зенона:
Если что-то движется, то оно движется либо в том месте, которое оно занимает, либо в том месте, где его нет. Однако оно не может двигаться в том месте, которое оно занимает (так как в каждый момент времени оно занимает все это место), но оно также не может двигаться и в том месте, где его нет. Следовательно, движение невозможно.
Этот парадокс называется стрела (в каждый момент времени летящая стрела занимает место, равное ей по протяженности, следовательно она не движется).
Наконец, существует четвертая апория, в которой речь идет о двух равных по длине колоннах людей, движущихся параллельно с равной скоростью в противоположных направлениях. Зенон утверждает, что время, за которое колонны пройдут друг мимо друга, составляет половину времени, нужного одному человеку, чтобы пройти мимо всей колонны.
Из этих четырех апорий первые три наиболее известны и наиболее парадоксальны. Четвертая просто связана с неправильным пониманием природы относительного движения.
Самый грубый и неизящный способ опровергнуть парадокс Зенона — это встать и пересечь комнату, обогнать черепаху или выпустить стрелу. Но это никак не затронет хода его рассуждений. Вплоть до XVII века мыслители не могли найти ключ к опровержению его хитроумной логики. Проблема была разрешена только после того, как Исаак Ньютон и Готфрид Лейбниц изложили идею дифференциального исчисления, которое оперирует понятием предел; после того как стала понятна разница между разбиением пространства и разбиением времени; наконец, после того как научились обращаться с бесконечными и бесконечно малыми величинами.
Возьмем пример с пересечением комнаты. Действительно, в каждой точке пути вам надо пройти половину оставшегося пути, но только на это вам понадобится в два раза меньше времени. Чем меньший путь осталось пройти, тем меньше времени на это понадобится. Таким образом, вычисляя время, нужное для того, чтобы пересечь комнату, мы складываем бесконечное число бесконечно малых интервалов. Однако сумма всех этих интервалов не бесконечна (иначе пересечь комнату было бы невозможно), а равна некоторому конечному числу — и поэтому мы можем пересечь комнату за конечное время.
Такой ход доказательства аналогичен нахождению предела в дифференциальном исчислении. Попробуем объяснить идею предела в терминах парадокса Зенона. Если мы разделим расстояние, которое мы прошли, пересекая комнату, на время, которое мы на это потратили, мы получим среднюю скорость прохождения этого интервала. Но хотя и расстояние, и время уменьшаются (и в конечном счете стремятся к нулю), их отношение может быть конечным — собственно, это и есть скорость вашего движения. Когда и расстояние, и время стремятся к нулю, это отношение называется пределом скорости. В своем парадоксе Зенон ошибочно исходит из того, что, когда расстояние стремится к нулю, время остается прежним.







 masterok
masterok
