Что такое параллельная математика

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

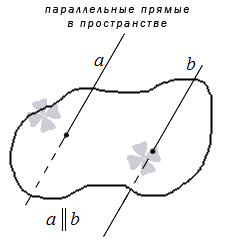
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

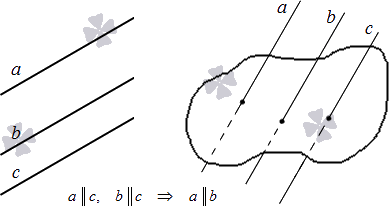
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

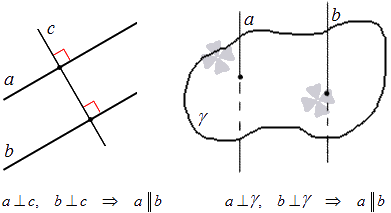
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Хокинг, математика и струны: три ключевых теории о параллельных мирах

Параллельные вселенные — это миры, которые гипотетически существуют одновременно с нашим, но не обязательно похожи на него. Есть предположения, что там действуют другие законы природы или события принимают альтернативные исходы: если в нашем мире подброшенная монета упала орлом вверх, то в другой реальности — решкой.

Научные гипотезы, содержащие конкретные обоснования существования параллельных вселенных, появились только в XX веке, но философы рассуждали на эту тему еще в античности. В V веке до нашей эры в Древней Греции возникла теория атомизма. Согласно этой теории любая материя состоит из химически неделимых частиц — атомов, хаотичное столкновение которых образует параллельные миры. Философ Хрисипп, живший в III веке до нашей эры, предполагал, что Вселенная постоянно умирает и возрождается, то есть одновременно существует бесконечное множество ее состояний.

Первым физиком, который высказал предположение о существовании параллельных реальностей, стал австрийский ученый Эрвин Шредингер. В 1952 году в Дублине он прочел лекцию по квантовой механике и ввел понятие суперпозиции — явления, при котором частица одновременно находится в нескольких разных состояниях.

Позже идею о мультивселенных стали использовать писатели-фантасты. Одна из первых книг на эту тему — роман Майкла Муркока «Расколотые миры» (1963). Чтобы разобраться, могут ли параллельные миры существовать на самом деле, а не только в литературе и кино, мы рассмотрели основные теории и поговорили с российскими физиками.

Теории параллельных Вселенных

Теория Хартла — Хокинга

В 1983 году физики Стивен Хокинг и Джеймс Хартл выпустили научную работу, посвященную новой теории возникновения Вселенной. С помощью квантовой механики ученые пытались объяснить, как мир мог появиться из ничего и что было до Планковской эпохи — самого раннего этапа в его развитии.

Стивен Хокинг посвятил почти всю свою научную карьеру космологии — разделу астрономии, изучающему появление и эволюцию Вселенной. Помимо исследовательских работ, он выпустил несколько научно-популярных книг на эту тему — «Краткая история времени», «Черные дыры и молодые вселенные», «Мир в ореховой скорлупке».

Согласно теории Хартла — Хокинга изначально наш мир находился в космологической сингулярности. Это состояние, для которого характерны бесконечно высокие плотность и температура вещества. В результате Большого взрыва Вселенная расширилась, образовались галактики, звезды, планеты. Она продолжает безгранично расширяться до сих пор.

Описывая мир, Хокинг и Хартл рассматривали Вселенную как квантовую систему, которая одновременно находится в бесконечном множестве состояний. Наша реальность — лишь одно из них. Помимо нее существуют параллельные миры, которые отображают все возможные исходы любых происходивших событий.

Идея, согласно которой система может находиться в нескольких состояниях в одно и то же время, объясняется мысленным экспериментом Эрвина Шредингера — одного из основателей квантовой механики. Ученый привел пример с кошкой в непрозрачном ящике рядом с атомом радиоактивного вещества, который с одной и той же вероятностью может распасться или не распасться, и устройством, которое убивает или не убивает животное в зависимости от состояния частицы. Для наблюдателя, пока тот не откроет ящик, кошка будет в равной степени живой и мертвой, то есть одновременно находиться в двух состояниях.

Математическая гипотеза Тегмарка

Астрофизик и профессор Массачусетского технологического института **Макс Тегмарк выдвинул гипотезу о том, что наш физический мир — это математическая структура: набор физических постоянных (например, число Авогадро, массы элементарных частиц) и уравнений, описывающих фундаментальные законы природы.

Ученый считает, что все непротиворечивые математические структуры, которые можно вычислить, существуют физически. Например, в нашем мире гравитационная постоянная равна 6,67430 (15) × 10−11 Н × м² / кг−2. В параллельной вселенной это значение может быть другим, а значит, меняются решения связанных с ним уравнений.

Объединяя свою и другие теории, Тегмарк предлагает четырехуровневую классификацию миров:

Теория струн

В 1970 году Йоитиро Намбу, Хольгер Нильсен и Леонард Сасскинд независимо друг от друга выдвинули предположение о том, что не все физические частицы можно считать точечными из-за нетипичного характера их взаимодействия. Исследователи предложили рассматривать некоторые элементарные частицы (например, пионы, которые по массе меньше атома) как тонкие протяженные нити — так называемые квантовые струны.

В 1984–1986 годах произошла суперструнная революция: физики поняли, что теорией струн гипотетически можно описать взаимодействие всех элементарных частиц, а не только пионов. Возникла идея, что квантовые нити колеблются с разными частотами и задают свойства материи, как привычные нам атомы.

Согласно общепринятой теории относительности Вселенная включает в себя четыре измерения, среди которых длина, ширина, глубина и время. По теории струн измерений может быть 6, 10 и даже 26. Но мы осознаем только четыре из них. Остальные измерения сворачиваются, но в них могут помещаться параллельные вселенные. Эта концепция в упрощенной визуальной форме отражена в фильме Кристофера Нолана «Интерстеллар» (2014).

Михаил Иванов, кандидат физико-математических наук, доцент кафедры теоретической физики МФТИ:

«Тема параллельных миров-вселенных в художественной и научной литературе переплетена с темой множественности миров-областей в пределах одной вселенной. Если рассматривать область якобы нашей вселенной, но отстающую от нас более чем на 14 млрд световых лет (это больше расстояния, которое свет может пройти с момента Большого взрыва к настоящему времени), тут уже возможно говорить о параллельных мирах.

Исторически одним из первых источников идеи мультивселенных была многомерная геометрия. Если в пространстве больше трех измерений, в нем можно представить несколько параллельных или пересекающихся гиперплоскостей, на каждой из которых действует обычная трехмерная физика. Восходят эти идеи минимум к XIX веку.

В современной науке основные источники идеи о мультивселенных — общая теория относительности и квантовая теория.

Общая теория относительности (ОТО) описывает, как геометрия пространства-времени, которая проявляется в виде гравитационных полей, изменяется со временем и взаимодействует с материей. В ней можно сконструировать решения основных уравнений так, чтобы черная дыра оказалась воротами в параллельный мир. Но это требует существования экзотических видов материи, которые едва ли возможны.

Можно применить обобщения ОТО к многомерному пространству и прийти к допущению, что в нем живут трехмерные браны (от слова мембрана), на поверхности которых размещаются параллельные вселенные. Можно модифицировать теорию так, чтобы пространство эволюционировало, порождая практически не связанные друг с другом области, в которых законы физики будут различаться.

В квантовой теории есть концептуальные проблемы, связанные с тем, что она состоит из двух разных частей. Первая — физика того, что происходит в замкнутой системе, обособленной от внешних взаимодействий. Вторая — теория измерений, описывающая взаимодействия системы с измерительным прибором.

Последнюю старались свести к физике замкнутых систем, включая в нее измерительный прибор. Но каждый раз теория измерений возникала снова, на другом уровне: вместо измерения состояния квантовой частицы приходилось рассматривать измерение состояния стрелки прибора или даже экспериментатора. В 1957 году американский физик Хью Эверетт III заметил, что теорию измерений можно исключить из квантовой механики, но тогда окажется, что в каждом эксперименте реализуются одновременно все возможные исходы. Это позволило проинтерпретировать теорию так, что Вселенная ветвится на варианты. В них происходит все, что в принципе могло бы произойти».

Существуют ли параллельные вселенные

Идею о существовании других реальностей в научном сообществе воспринимают неоднозначно. Сторонники этой концепции — Стивен Хокинг, американские физики-теоретики Брайан Грин и Ли Смолин, американский космолог Александр Виленкин.

Аргументы за:

Против идеи о параллельных вселенных выступают британский космолог Джордж Эллис, американские физики-теоретики Стивен Вайнберг и Дэвид Гросс. Их главный аргумент в том, что она ненаучна в целом. Ни одну из описанных выше теорий невозможно опровергнуть экспериментально, а значит, и доказать.

Михаил Иванов:

«В обозримом будущем мы едва ли сможем доказать существование параллельных вселенных. Многие теории основаны больше на игре ума, чем на экспериментальных фактах. Доказательство других порой требует ускорения элементарных частиц до энергии Планка (500 кг в тротиловом эквиваленте) или наблюдения за ними в течение миллиардов лет.

Более важный вопрос — удастся ли нам сформулировать квантовую теорию гравитации. Есть вероятность, что с ней мы сможем создавать параллельные вселенные, даже если раньше их не существовало».

В интервью для журнала Scientific American Джордж Эллис объяснил, что, по его мнению, ученые предложили идею о параллельных вселенных как универсальное объяснение природы нашего существования. Эту концепцию нельзя назвать неправильной, но она носит чисто философский, а не научный характер.

Станислав Алексеев, доктор физико-математических наук, ведущий научный сотрудник отдела релятивистской астрофизики Государственного астрономического института имени П. К. Штернберга:

«У идеи о существовании параллельных вселенных есть несколько причин. Например, наличие черных дыр — каналов, через которые гипотетически энергия попадает из нашего мира в другой. Противоположные им белые дыры, существование которых не доказано, но допускается, могут быть источниками излучения из параллельных вселенных.

С точки зрения космологии, наличие других вселенных — возможность нарушить закон сохранения энергии, показав каналы, через которые она может убывать и прибывать. Это могло бы объяснить проблему космических лучей, энергия которых выше теоретического верхнего предела, без нарушения лоренц-инвариантности — свойства физической величины оставаться неизменной при преобразованиях.

Для доказательства или выбора одной из вышеописанных теорий не хватает экспериментальных, наблюдательных данных. В настоящее время во всех проектах общая теория относительности (ОТО) подтверждается с высокой точностью, но возможно, что в будущем удастся экспериментально выйти за ее границы».

Как современная наука изучает возможность существования параллельных Вселенных

В 1998 году во время наблюдения за сверхновыми звездами была обнаружена темная энергия. Это форма энергии, которая заполняет пустое пространство и действует противоположно гравитации, то есть отталкивает тела, а не притягивает их. За счет нее Вселенная расширяется с ускорением.

Ученые из Даремского и Сиднейского университетов создали компьютерную модель развития Вселенной и пришли к выводу, что в нашем мире относительно мало темной энергии. Согласно теориям возникновения Вселенной, ее должно было быть настолько много, что галактики и звезды не могли сформироваться, а жизнь не появилась бы.

В 2015 году в научном издании The International Journal of Physics вышла статья ученого А. А. Антонова о том, что темная энергия может быть признаком существования других вселенных. Для проверки этой и других теорий, связанных с темной энергией, ученые Национальной лаборатории имени Лоуренса в Беркли, США, создали прибор Dark Energy Spectroscopic Instrument, который исследует электромагнитные спектры далеких галактик. Впервые он начал работу в 2019 году.

Источник

Что такое параллельная математика

Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.

Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).

Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.

Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Свойства и признаки параллельных прямых

Свойства и признаки параллельных прямых:

Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.

Это конспект по теме «Параллельные прямые». Выберите дальнейшие действия:

Источник