Что такое параллельные и перпендикулярные прямые

Геометрия. 7 класс

Конспект урока

Параллельные и перпендикулярные прямые

Перечень рассматриваемых вопросов:

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Перпендикулярные прямые – две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.

Теоретический материал для самостоятельного изучения.

Взаимное расположение двух прямых на плоскости.

Вспомните, как могут располагаться на плоскости две прямые.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Углы, изображенные на рисунке:

Накрест лежащие: 3 и 5; 4 и 6.

Соответственные: 1 и 5; 2 и 6; 3 и 8; 4 и 7.

Односторонние: 3 и 6; 4 и 5.

Признаки и свойства параллельных прямых.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Это признаки параллельности прямых. Обратные теоремы верны и представляют свойства параллельных прямых.

Способ построения параллельных прямых:

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей, то они параллельны.

Если две прямые, пересекаясь, образуют четыре прямых угла, они называются перпендикулярными.

Прямые а и b на рисунке перпендикулярны: а ⏊ b.

Через каждую точку можно провести прямую, перпендикулярную данной и притом только одну.

Это можно сделать, пользуясь угольником или транспортиром.

Перпендикулярность и параллельность прямых.

Две прямые, перпендикулярные к третьей не пересекаются т. е параллельны между собой.

Отрезок АВ, перпендикулярный к прямой а, называют перпендикуляром. Точка В – основание перпендикуляра.

Из любой точки, не лежащей на данной прямой, можно опустить перпендикуляр на эту прямую и притом только один.

Длину перпендикуляра АВ называют расстоянием от точки А до прямой а.

Расстоянием между параллельными прямыми называют расстояние АВ от любой точки одной прямой до другой прямой.

Разбор заданий тренировочного модуля.

№ 2. Докажите, что биссектрисы смежных углов перпендикулярны.

Источник

Перпендикулярные прямые

Рассмотрим две пересекающиеся прямые. Они образуют четыре неразвернутых угла.

Утверждение 1. Если один из углов пересекающих прямых − прямой, то остальные три угла также прямые.

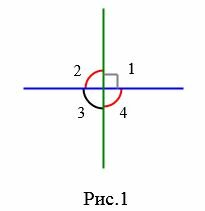Доказательство. Пусть угол 1 прямой (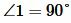)(Рис.1). Поскольку углы 1 и 2 смежные, то

Углы 2 и 4, а также 1 и 3 вертикальные. Тогда

, .

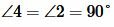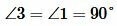Таким образом углы 1, 2, 3, 4 прямые.

Определение 1. Две пересекающиеся прямые называются перпендикулярными (взаимно перпендикулярными), если они образуют четыре прямых угла.

Если прямые AB и CD перпендикулярны, то это обозначается:

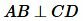и читается так: «прямая AB перпендикулярна прямой CD«.

Теорема 1. Если две прямые перпендикулярны к третьей, то они не пересекаются.

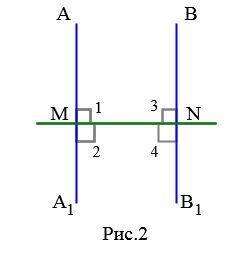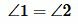
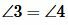
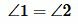
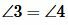
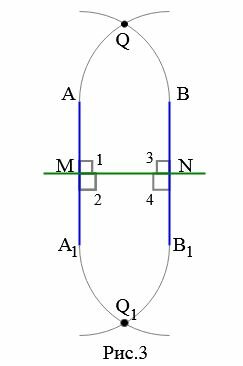Доказательство. Прямые AA₁ и BB₁ перпендикулярны к прямой MN (Рис.2). Тогда (определение 1). Аналогично . Перегнем мысленно рисунок по прямой MN так, чтобы верхняя часть рисунка наложилась на нижнюю. Из и следует, что луч MA наложится на луч MA₁, а луч NB − на NB₁.

Предположим, теперь, что прямые AA₁ и BB₁ пересекаются в некоторой точке Q (Рис.3). Тогда эта точка наложится на некоторую точку Q₁. Получается, что через две точки Q и Q₁ проходят две прямые AA₁ и BB₁. Но это невозможно. Следовательно предположение, что прямые AA₁ и BB₁ пересекаются неверно. То есть они не пересекаются.

Источник

Параллельные и перпендикулярные прямые

Определение.Две прямые на плоскости называются параллельными, если они не пересекаются.

Если прямая а параллельная прямой b, то пишут а || b.

Рассмотрим некоторые свойства параллельных прямых, и прежде всего признаки параллельности.

Признаками называют теоремы, в которых устанавливается наличие какого-либо свойства объекта, находящегося в определенной ситуации. В частности, необходимость рассмотрения признаков параллельности прямых вызвана тем, что нередко в практике требуется решить вопрос о взаимном расположении двух прямых, но в то же время нельзя непосредственно воспользоваться определением.

Рассмотрим следующие признаки параллельности прямых:

1.Две прямые, параллельные третьей, параллельны друг другу.

2.Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Справедливо утверждение, обратное второму признаку параллельности прямых: если две параллельные прямые пересечены третьей, то внутренние накрест лежащие углы равны, а сумма односторонних углов равна 180°.

Важное свойство параллельных прямых раскрывается в теореме, носящей имя древнегреческого математика Фалеса: если параллельные прямые, пересекающие стороны угла отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

Если прямая а перпендикулярна прямой b, то пишут а ± b. Основные свойства перпендикулярных прямых нашли отражение в двух теоремах:

1. Через каждую точку прямой можно провести перпендикулярную к ней прямую, и только одну.

2. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий концом их точку пересечения. Конец этого отрезка называется основанием перпендикуляра.

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.

Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой.

Треугольники

Первые упоминания о треугольнике и его свойствах содержатся в египетских папирусах. Например, в них предлагается находить площадь равнобедренного треугольника как произведение половины основания на боковую сторону, хотя для любого равнобедренного треугольника с малым углом при вершине, противоположной основанию, такой способ дает приближенное значение площади.

Рассмотрим основные понятия, связанные с треугольником.

Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соеди­няющих их отрезков.

Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником (или плоским треугольником).

В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии.

Углом треугольника АВС при вершине А называется угол, образованный полупрямыми АВ и АС.

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.

Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.

На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающими более быстрое решение вопроса об отношениях между ними. Таких признаков три.

1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.

Равнобедренные треугольники обладают рядом свойств, например:

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Отметим еще несколько важных свойств треугольников.

1. Сумма углов треугольника равна 180°.Из этого свойства следует, что в любом треугольнике хотя бы два угла острые.

2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.

3. В любом треугольнике каждая сторона меньше суммы двух других сторон.

Для прямоугольного треугольника с углом 30° справедливо следующее свойство: катет, противолежащий этому углу, равен половине гипотенузы.

Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Четырехугольники

Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называют четырехугольником (или плоским четырехугольником).

Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.

Источник

Математика

Урок 1: Перпендикулярные прямые и параллельные прямые

Перпендикулярные прямые и параллельные прямые

Изучая геометрические фигуры, мы постоянно сталкиваемся с перпендикулярными прямыми. Например, смежные стороны прямоугольника перпендикулярны. Как убедиться в том, что две линии (прямые) перпендикулярны? С давних пор люди проверяли перпендикулярность стены основанию дома с помощью специального отвеса. Отсюда и произошло название перпендикуляра: латинское «перпендикулярис» означает «отвесной». Чтобы построить перпендикуляр к прямой, необходимо построить прямой угол. Это можно сделать с помощью чертежного треугольника или транспортира.

Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

На рисунке изображены прямые а и b, они перпендикулярны друг другу и осям координат. Пишут: a ⊥ b (а перпендикулярна b), a ⊥ OY (прямая a перпендикулярна оси ОY), b ⊥ OX (прямая b перпендикулярна оси ОХ).

На рисунке прямые c и d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут: с ⊥ d. Отрезки (или лучи), лежащие на перпендикулярных прямых, называют перпендикулярными отрезками (или лучами). Например, луч ОХ ⊥ лучу ОY.

Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться.

Две непересекающиеся прямые на плоскости называют параллельными.

Пишут а || b. Эту запись читают так: «Прямая а параллельна прямой b».

Отрезки (лучи), лежащие на параллельных прямых, называют параллельными отрезками (лучами).

АВ || CM (отрезок АВ параллелен отрезку СМ).

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

Поэтому противоположные стороны любого прямоугольника параллельны.

Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Пример 1. Начертим два перпендикулярных отрезка АВ и СМ так, чтобы они не пересекались; пересекались.

Пример 2. Начертим треугольник и проведем через каждую вершину прямую, параллельную противоположной стороне.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 8 Перпендикулярность прямой и плоскости

Перечень вопросов, рассматриваемых по теме

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости

Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень

Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.

Открытые электронные ресурсы:

Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.

Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.

Теоретический материал для самостоятельного изучения

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.

По лемме о перпендикулярности двух параллельных прямых к третьей а₁ ⊥ x.

Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а₁ ⊥ α

Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.

Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а.

Докажем, что прямая b₁ совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b₁ и b не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b₁ ∊ β, α β = c (невозможно)→ а ‖ b

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.

Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.

Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.

Предположим, что существует прямая с₁, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с₁ перпендикулярны плоскости α. Значит, прямые с и с₁ параллельны. Но по построению прямые с и с₁пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.

Теоретический материал для углубленного изучения

Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Доказательство (см. рис. 1)

Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.

Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.

Примеры и разборы решения заданий тренировочного модуля

Выбор элемента из выпадающего списка

Выпишите ребра, перпендикулярные плоскости (DC).

Правильный вариант/варианты (или правильные комбинации вариантов):

Неправильный вариант/варианты (или комбинации):

Подсказка: в кубе все углы по . Плоскость (DC), проходит через грань куба DC.

Закончите предложение, чтобы получилось верное утверждение.

Правильный вариант/варианты (или правильные комбинации вариантов):

Две прямые называются перпендикулярными, если …

угол между ними равен 90

Если плоскость перпендикулярна одной из двух параллельных прямых, то она …

перпендикулярна и другой

Неправильный вариант/варианты (или комбинации):

Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.

Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Источник