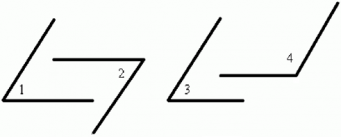Что такое параллельные углы
Виды и отношения углов
Развёрнутый угол и угловой градус
Развёрнутый угол — это угол, образованный двумя дополнительными полупрямыми. Развёрнутый угол принимаем равным 180°. Таким образом один угловой градус — это 1/180 часть развёрнутого угла.
AB и AC — это две дополнительные полупрямые, образующие развёрнутый угол BAC. Двигай луч AB.
Виды углов
Острый угол больше 0°, но меньше 90°. Тупой угол больше 90°, но меньше 180°. Прямой угол равен 90°.
Угол ABC — острый. Двигай точки A, B и C. Угол DEF — тупой. Двигай точки D, E и F. Угол GHI — прямой. Двигай точки G, H и I.
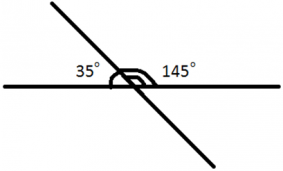
Смежные углы
Смежные углы это такие углы, у которых одна сторона общая, а две другие — дополнительные полупрямые.
Здесь углы BAC и CAD — смежные. У них сторона AC — общая, а стороны AB и AD — дополнительные полупрямые.
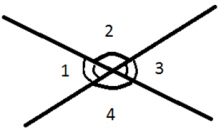
Вертикальные углы
Вертикальные углы — это углы, у которых стороны одного угла являются дополнительными полупрямыми к сторонам другого угла.
Здесь углы BAC и DAE — вертикальные. У них сторона AB — дополнительная полупрямая к стороне AD, а сторона AC — дополнительная полупрямая к стороне AE. Двигай точки A, B и C.
Соответственные углы при пересечении двух параллельных прямых секущей.
При пересечении двух параллельных прямых секущей соответственные углы — это углы, у которых стороны, лежащие на параллельных прямых, сонаправлены, и стороны, лежащие на секущей, сонаправлены.
Через точку C проходит прямая, параллельная прямой AB. Двигай точки A, B и C. Тронь внутреннюю область угла, чтобы выделить этот угол и соответственный ему угол.
Односторонние углы при пересечении двух параллельных прямых секущей.
При пересечении двух параллельных прямых секущей односторонние углы — это углы, у которых стороны, лежащие на параллельных прямых, сонаправлены, а стороны, лежащие на секущей, противоположно направлены.
Через точку C проходит прямая, параллельная прямой AB. Двигай точки A, B и C. Тронь внутреннюю область угла, чтобы выделить этот угол и односторонний с ним угол.
Накрест лежащие углы при пересечении двух параллельных прямых секущей.
При пересечении двух параллельных прямых секущей накрест лежащие углы — это углы, у которых стороны, лежащие на параллельных прямых, противоположно направлены, и стороны, лежащие на секущей, противоположно направлены.
Через точку C проходит прямая, параллельная прямой AB. Двигай точки A, B и C. Тронь внутреннюю область угла, чтобы выделить этот угол и накрест лежащий с ним угол.
Что такое параллельные углы
Две прямые называются параллельными (обозначение: \(a||b\)), если они не имеют общих точек (не пересекаются).
Аксиома параллельности
Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Из аксиомы параллельности и признаков параллельности прямых следует теорема : через точку, не лежащую на данной прямой, можно провести ровно одну прямую, параллельную данной.
Названия углов при двух прямых и секущей
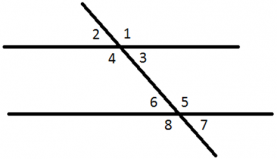
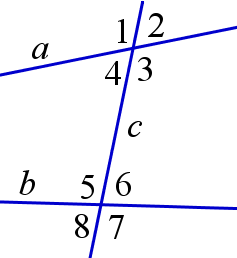
Пусть прямая \(c\) пересекает каждую из прямых \(a\) и \(b\). Образующися при этом пары углов, отмеченных на рисунке, имеют следующие названия.
1 и 5, 2 и 6, 3 и 7, 4 и 8 – соответственные;
3 и 5, 4 и 6 – внутренние накрест лежащие;
4 и 5, 3 и 6 – внутренние односторонние;
1 и 7, 2 и 8 – внешние накрест лежащие;
1 и 8, 2 и 7 – внешние односторонние.
Признаки параллельности прямых
1. Если внутренние накрест лежащие углы при двух прямых и секущей равны, то эти две прямые параллельны.
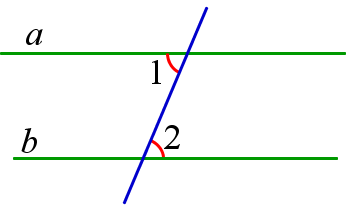
2. Если сумма внутренних односторонних углов при двух прямых и секущей равна \(180^<\circ>\), то эти две прямые параллельны.
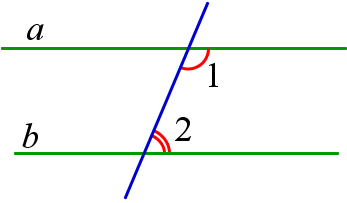
3. Если соответственные углы при двух прямых и секущей равны, то эти две прямые параллельны.
4. Если внешние накрест лежащие углы при двух прямых и секущей равны, то эти две прямые параллельны.
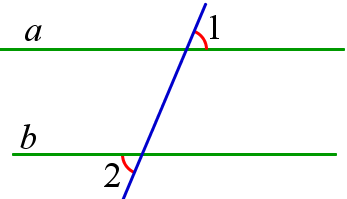
5. Если сумма внешних односторонних углов при двух прямых и секущей равна \(180^<\circ>\), то эти две прямые параллельны.
6. Если две прямые перпендикулярны третьей прямой, то они параллельны друг другу.
Свойства углов при параллельных прямых и секущей
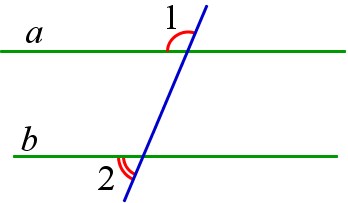
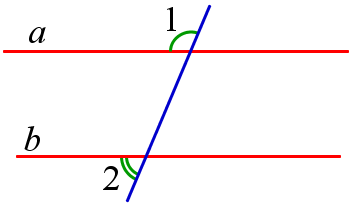
1. Внутренние накрест лежащие углы при параллельных прямых и секущей равны.
$$ a||b \, \Rightarrow \, \angle<1>=\angle <2>$$
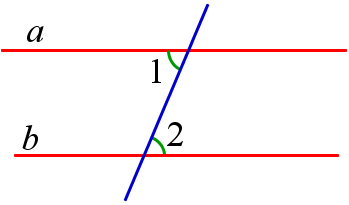
2. Сумма внутренних односторонних углов при параллельных прямых и секущей равна \(180^<\circ>\).
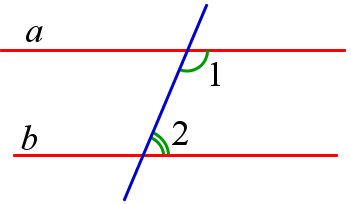
3. Соответственные углы при параллельных прямых и секущей равны.
$$ a||b \, \Rightarrow \, \angle<1>=\angle <2>$$
4. Внешние накрест лежащие углы при параллельных прямых и секущей равны.
$$ a||b \, \Rightarrow \, \angle<1>=\angle <2>$$
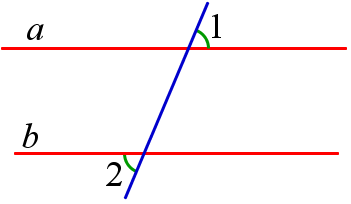
5. Сумма внешних односторонних углов при параллельных прямых и секущей равна \(180^<\circ>\).
6. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Соответственные углы равны, то есть
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!

Периметр параллелограмма — это сумма всех его сторон, то есть

Углы и — односторонние при параллельных прямых и секущей, следовательно,
51. Планиметрия  Читать 0 мин.
Читать 0 мин.
51.65. Углы и параллельные прямые
Взаимное расположение прямых:
При пересечении двух прямых образуются вертикальные и смежные углы.
Вертикальные углы — равны.
Сумма смежных углов равна 180°.
Параллельные прямые
Прямые называются параллельными, если они не пересекаются, сколько бы их не продолжать.
О параллельных прямых:
При пересечении двух параллельных прямых секущей образуются следующие углы:
Часто для использования свойств углов, полученных при пересечении двух параллельных прямых секущей, необходимо применять дополнительные построения.
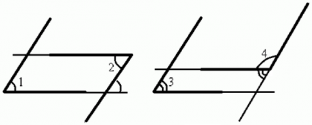
Пример: Даны углы с попарно параллельными сторонами. Что можно сказать об углах 1 и 2? Что можно сказать об углах 3 и 4?
Продолжим стороны углов до пересечения:
Получаем, что углы 1 и 2 равны, т. к. являются накрест лежащими при параллельных прямых.
Сумма углов 3 и 4 равна 180°, т. к. они являются односторонними при параллельных прямых.
Теорема Фалеса: При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки (образуются подобные треугольники).
Углы при параллельных прямых и секущей — виды и свойства
Изучаемый геометрический объект

Прежде чем рассматривать углы, которые образуются в результате различного взаимного расположения прямых на плоскости, следует подробно изучить сам геометрический объект. Любая прямая линия представляет собой набор точек в пространстве любой мерности, каждая из которых может быть получена из предыдущей путем ее переноса на вектор, имеющий конкретное направление.
Рассматриваемый объект является одномерным, то есть он имеет лишь один единственный размер, который отличен от нуля. Прямая — это бесконечная линия, любые две точки на которой отсекают отрезок определенной длины.
Векторное представление
Определение прямой говорит о том, что для универсального ее математического описания следует воспользоваться понятием вектора. Под ним в математике подразумевают направленный отрезок, имеющий начало и конец. В двумерном пространстве любой вектор представляется набором двух чисел, например, a (a1, a2). Построить его можно следующим образом:

Самостоятельно вектор не может задать прямую, поскольку существует бесконечное множество объектов a (a1, a2), которые получаются с помощью параллельного переноса их по всей плоскости. Необходима фиксированная точка, чтобы привязать начало направленного отрезка. Так образуется прямая линия. Ее векторное уравнение может быть записано в следующем виде:
A (x, y) = A0 (x0, y0) + alfa*(a1, a2).
Здесь A (x, y) — произвольная точка линии, A0 (x0, y0) — фиксированная точка на ней, (a1, a2) — координаты вектора, который называется направляющим, alfa — любое рациональное число, которое показывает, на какую долю направленного отрезка (a1, a2) следует переместить A0 (x0, y0), чтобы попасть в A (x, y).
Другие формы уравнений
Векторное уравнение прямой является неявным по отношению к координатам x и y. Для одних задач его удобно использовать, для других же следует применять иные формы записи. Одной из них является параметрическая. Ее можно записать так:
Этой формой удобно пользоваться для определения конкретных координат x и y. Если из этой системы равенств выразить параметр alfa, то можно получить симметричное уравнение прямой:
Наконец, если представить это выражение таким образом, чтобы y был выражен, как функция от x, то получится общее представление прямой линии в двумерной системе координат:
y = a2/a1*x + (y0-a2/a1*x0).
Эта формула известна любому школьнику, поскольку основное внимание при изучении геометрических свойств рассматриваемого одномерного объекта в школах уделяется именно ей. Зная, как перевести один вид уравнения прямой в другой, можно выполнять соответствующие преобразования для решения конкретных задач.
Взаимное расположение
Рассматривая вопрос параллельных углов, следует изучить все возможные варианты расположения на плоскости прямых линий. Количество ситуаций зависит от числа присутствующих геометрических объектов, а также от размерности координатной системы.
Две прямые
На плоскости существует три разных варианта расположения двух прямых относительно друг друга. К ним относятся следующие:

Три прямые
Когда на плоскости имеются три прямых, то количество вариантов их взаимного расположения возрастает. Возможные следующие случаи:
Для определения всех этих ситуаций следует проводить геометрический анализ с применением уравнений разных форм представления прямых. Случай номер 2 является наиболее интересным, поскольку в результате такого взаимного расположения образуется набор специальных углов.
Секущая и углы
В школьном курсе геометрии изучение прямых и секущей имеет особый интерес. В результате такого расположения одномерных объектов получаются несколько углов, обладающих специальными свойствами. Полученные выводы используются для решения не только теоретических, но и практических вопросов.
Выделяют три типа углов, образующихся при пересечении секущей двух параллельных линий:

Один из накрест лежащих углов расположен во внутренней области параллельных линий с одной стороны от секущей, второй же лежит во внешней области с другой стороны. Поскольку секущая пересекает каждую параллельную, образуется четыре пары рассматриваемых углов, которые лежат друг относительно друга накрест. Попарно эти углы равны. Две пары из них являются тупыми, а две — острыми. Особый случай составляют вертикальные прямые углы.
Односторонние — это такие углы, которые бывают между параллельными линиями и только с одной стороны от секущей (отсюда их название). Причем один из них образован одной параллельной прямой, а другой относится к другой параллельной линии. Они в общем случае не равны друг другу, поскольку один является острым, а другой тупым. Однако если секущая перпендикулярна параллельным прямым, то односторонние углы будут составлять 90 градусов. Их важное свойство состоит в том, что в сумме всегда получается 180 градусов. В рассматриваемом расположении одномерных объектов существует лишь две пары этих углов.
Соответственные углы при параллельных прямых лежат по одну сторону от секущей, но по разные стороны от каждой параллельной прямой. Они также являются смежными. Их существует четыре пары, которые попарно одинаковы. Их сумма в каждой паре всегда равна 180 градусам.
Следует запомнить, что соответственные углы всегда лежат по одну сторону от секущей. В указанном расположении прямых можно найти еще четыре пары смежных углов, которые, однако, будут располагаться по разные стороны от секущей и по одну сторону от параллельной линии. Они соответствующими не являются.
Методы вычисления
Зная значение любого из накрест лежащих, односторонних и соответственных углов, можно найти величины всех остальных, воспользовавшись их свойствами. Для проведения вычислений проще всего воспользоваться векторной формой представления прямых.
Пусть существует две параллельных линии, которые заданы следующим образом:

Секущая задается векторным уравнением: C (x, y) = С0 (x3, y3) + l*(c1, c2). Для расчета угла пересечения любых двух прямых необязательно искать их общую точку, достаточно воспользоваться свойствами умножения направляющих векторов. Они могут перемножаться двумя различными способами:
Пусть следует найти угол пересечения прямых A и C. Для скалярного произведения можно записать: ((a1, a2)*(c1, c2)) = a1*c1 + a2*c2 = ((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5*cos (teta). Откуда получается неизвестный угол teta:
teta = arccos ((a1*c1 + a2*c2)/(((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5)).
Другой способ определения teta заключается в применении векторного произведения. Получается следующее выражение: [(a1, a2)*(c1, c2)] = a1*c2 — a2*c1 = ((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5*sin (teta). Тогда teta может быть вычислен по формуле:
teta = arcsin ((a1*c2 — a2*c1)/(((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5)).
Вычислить соответствующие функции арксинуса или арккосинуса можно с использованием инженерного калькулятора. Как только известен угол пересечения секущей и параллельной прямых, остальные углы находятся с помощью добавления или вычитания его из 180 градусов, согласно их свойствам.
Пример решения задачи
Прежде чем перейти к использованию скалярного или векторного произведения, следует найти направляющие отрезки для каждой из прямой. Сначала каждую из них нужно записать в параметрической форме:

Откуда получаются координаты направляющего вектора: (-0,5, 1). Проведение аналогичных преобразований для второй линии приводит к ее направляющему отрезку с координатами (1, 1).
Воспользовавшись формулой для угла teta через скалярное произведение, можно получить следующий результат:
teta = arccos ((-0,5*1 + 1*1)/(((-0,5)^2+(1)^2)^0,5*((1)^2+(1)^2)^0,5)) = 71,6 градуса.
Тогда накрест лежащие углы составят 71,6 градуса, а односторонние и соответствующие будут равны 71,6 и 108,4 градуса (180−71,6).
Знание уравнений прямых и умение производить операции умножения векторов позволяет вычислять любые типы углов, которые образуются при пересечении параллельных прямых секущей линией. Подобные расчеты можно проводить не только в двумерном, но также в трехмерном пространстве.


 Читать 0 мин.
Читать 0 мин.