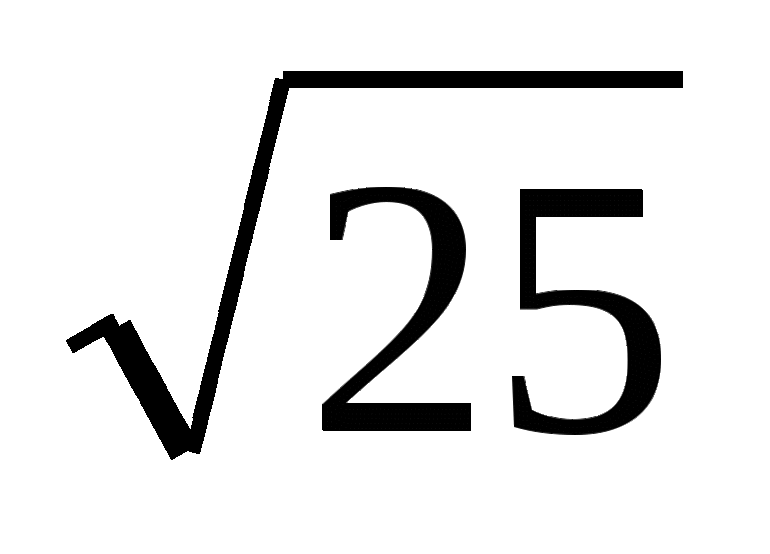Что такое параметр в алгебре 9 класс

Что такое параметр? Простые задачи с параметрами

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Разложим левую часть неравенства на множители:

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Источник

Решение задач с параметрами в курсе алгебры. 7–9-е классы

Разделы: Математика

В курсе алгебры 7 класса в параграфе «Линейное уравнение с одной переменной» следует разобрать решение уравнения ах = в с неизвестным х как уравнение параметрами а и в. Здесь учащихся следует познакомить с понятием «параметры» (те переменные а, в, с, :, которые при решении уравнения считаются постоянными, или те коэффициенты, которые заданы не конкретными числами, а обозначены буквами).

На уроках обобщения, следующих за этим параграфом возможно разобрать решение линейного уравнения ах + в = с с неизвестным х и параметрами а, в, с.

В течение учебного года можно предлагать для решения задания следующего типа.

Знакомить учащихся с решением систем линейных уравнений с параметрами следует начинать после изучения параграфа «Системы линейных уравнений с двумя переменными», котором разбирается графический способ решения систем линейных уравнений.

Предлагаются следующие задания.

Подобрать значения параметров а и в, чтобы:

а) система имела единственное решение;

б) система не имела решений

1) 2) 3) 4) 5)

Работая с последней системой, следует подробнее разобрать ответы на поставленные вопросы.

Решение. 1) если , то система примет вид

если т.е. система имеет единственное решение;

если = и т.е. и система не имеет решения;

2) если система примет вид и имеет единственное решение.

Ответ: если система имеет единственное решение;

если , , то система не имеет решения.

Решите систему уравнений с параметрами к и р, если :

1) 2)

Решение первой системы получается из знания взаимного расположения графиков линейных функций ( Ответ: (0;3)), решение второй системы предполагает умение решать системы линейных уравнений аналитическим методом.

При всех значениях параметра а решить систему уравнений

1) если , т.е. , то данная система равносильна

Решите систему уравнений с двумя неизвестными х и у:

3) Ответ: при , то х=а-1, у=а;

Задачи с параметрами для решения в 8 классе предполагают знания по теме «Квадратные уравнения», «Дробные рациональные уравнения», «Неравенства».

Задачи с параметрами, дополняющие список задач из учебника к теме «Квадратные уравнения».

Найдите к и второй корень уравнения:

Найдите все числа р и с такие, что корни уравнения х 2 + рх + с =0, равны р и с.

Решите уравнение ах 2 =1.

Задания с параметрами, предлагаемые для выполнения после изучения темы «Неравенства».

1. Найдите все значения параметра а, для которых квадратное уравнение (а+1)х 2 + 2(а+1)х+а-2=0 а) имеет два различных корня;

в) имеет два равных корня.

3. Решите уравнение ах 2 + 2х + 1 = 0.

а) имеет два различных корня;

5. Найдите все значения параметра а, для которых уравнение имеет единственный корень

б) ах 2 + (4а+2)х + 3а + 3/2 = 0.

После изучения главы I «Рациональные дроби» можно предлагать учащимся решать более сложные системы линейных уравнений с параметрами.

1. При всех значениях параметров а и в решить систему

1) 2) 3) 4) 5) 6)

если , , то ;

Ответ: если , то (; )

В 9 классе представляется целесообразным после изучения главы I «Квадратичная функция» вернуться к решению уравнений второй степени с параметрами, предлагая учащимся для решения задания следующего типа.

1. Решите квадратные уравнения.

2) ах 2 + (а + 1)х +а 2 +а = 0;

3) ах 2 + 2х(а + 1) + а +3 = 0;

2. Найдите все значения а, при которых уравнение имеет хотя бы один корень.

4. Найдите все значения в, при которых уравнение имеет два различных корня.

В конце учебного года в 9 классе на уроках «Повторение:» нужно познакомить учащихся с графическим методом решения уравнений 2-ой степени с параметрами, научить распознавать положение параболы на плоскости в зависимости от коэффициентов.

Для этого необходимо напомнить:

Знак коэффициента а показывает направление ветвей параболы;

Указанные свойства парабол позволяют получить следующие факты, касающиеся расположения корней квадратного трехчлена на числовой оси.

1. Корни квадратного трехчлена х₁ и х₂ (f(х) = ах 2 +вх+с) будут строго меньше числа М, если выполняются следующие условия (очевидные, благодаря рисунку).

2. Если М I R, то х₁ 0

a>0, f(M) 2 +вх+с принадлежат интервалу(М;N), если и только если выполняются условия:

Задания, соответствующие другим случаям расположения корней квадратного трехчлена (оба корня больше некоторого числа М; если отрезок [М; N] целиком лежит на интервале (х₁;х₂) и другие) решаются, следуя аналогичным требованиям, проиллюстрированным на рисунке, который отвечает конкретному заданию.

.

Ответ: .

3. При каких значениях а один корень уравнения ах 2 +х +1 = 0 больше 2, а другой меньше 2?

Ответ: .

Ответ: .

Ответ: таких а не существует.

Ответ: .

Ответ: .

Ответ: .

Источник

Параметры в математике 9 класс.

Описание презентации по отдельным слайдам:

Тема: параметры в математике 9 класс. Учитель Науменкова О.В.

Ц е л ь: рассмотреть возможности применения графического метода при решении задач с параметрами.

Что называется параметром? Это независимая переменная, значения которой в задаче считается заданным, фиксированным или произвольным действительным числом. Что значит решить уравнение с параметром? Для каждого значения параметра найти множество решений уравнения.

При каком значении параметра а уравнение не имеет корней?

Задайте аналитически множество точек плоскости.

Задайте аналитически множество точек плоскости.

Задайте аналитически множество точек плоскости.

Какая ошибка допущена при построении графика

Какая ошибка допущена при построении графика

Какая ошибка допущена при построении графика

Что значит решить уравнение f(x)=g(x) графическим способом? При решении уравнения f(x)=g(x) графическим способом строится графики функции y=f(x) и y=g(x) в одной системе координат. Корнями уравнения являются точки пересечения данных графиков.

Что значит решить уравнение f(x)=a графическим способом? При решении уравнения f(x)=a графическим способом строятся графики функции y=f(x) и y= a в одной системе координат. Если график функции не зависит от параметра, то он неподвижен, а если зависит, то представляет собой множество прямых параллельных оси абсцисс.

При каком значении параметра р система имеет три решения? При р=– 2

Что нового вы узнали на уроке? Чему научились? Что поняли? Что понравилось?

Итог урока Применение графического метода делает решение уравнения с параметром: наглядным; более легким; более красивым и изящным. Графические построения помогают осмыслить решение уравнения с параметрами.

Спасибо за внимание!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-949137

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Хабаровске родители смогут заходить в школы и детсады только по QR-коду

Время чтения: 1 минута

Большинство родителей в России удовлетворены качеством образования в детсадах

Время чтения: 2 минуты

Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах

Время чтения: 5 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Чем заняться с детьми в новогодние праздники в Москве

Время чтения: 4 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

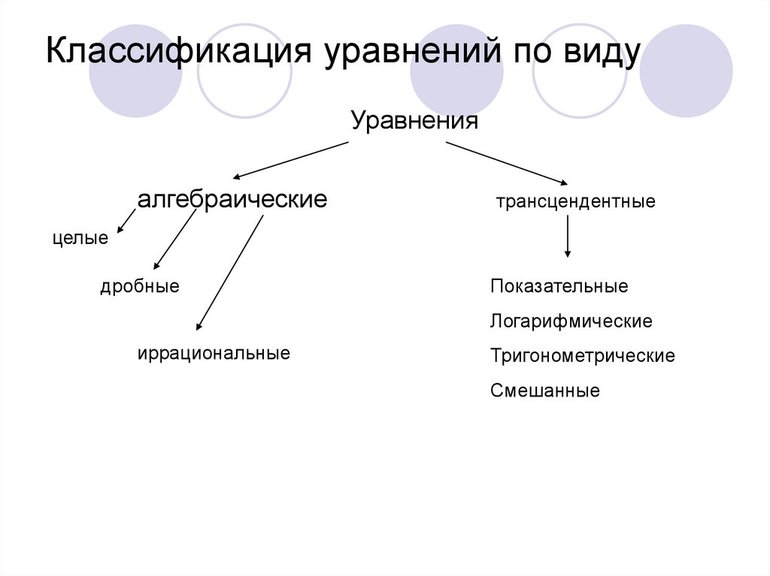
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

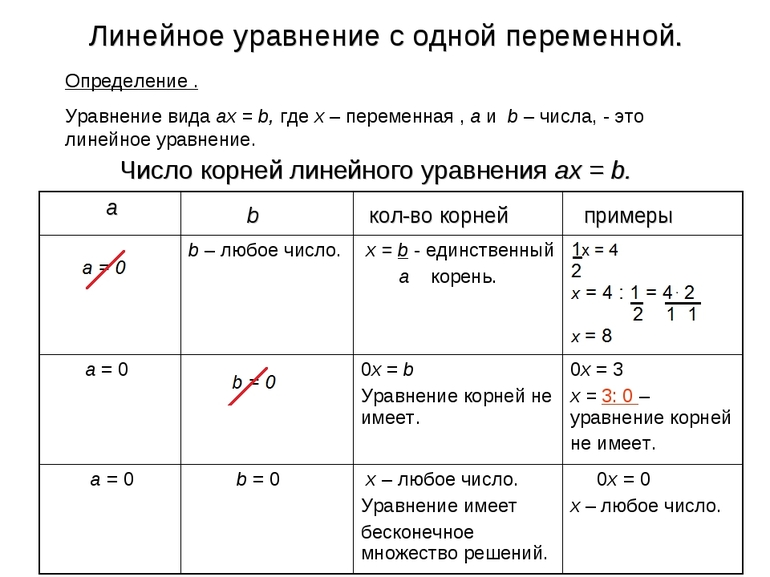
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

Источник