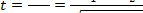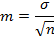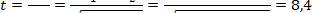Что такое параметрические критерии
Параметрические критерии
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ПРЕПОДАВАТЕЛЯ
По дисциплине «Доказательная медицина»
для специальности 060101–Лечебное дело (очная форма обучения)
К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ № 5
ТЕМА: «Методы сравнительной статистики»
Утверждена на кафедральном заседании
протокол № __3__ от «_12_» октября 2011 г.
Заведующий кафедрой к.м.н., доцент________(подпись) Шульмин А.В.
к.м.н., доцент ________ (подпись) Козлов В.В.
к.ф-м.н., доцент ________(подпись) Аршукова И.Л.
ассистент ________ (подпись) Добрецова Е.А.
Допустим, что удается заметить какие-либо численные различия в характеристиках сравниваемых рядов. Первым делом возникает вопрос: какова вероятность, что эти различия неслучайны, и будут систематически повторяться в дальнейшем при воспроизведении условий эксперимента или наблюдения, т.е. выявленные различия являются статистически значимыми.
Выбор подходящего метода сравнения выборочных совокупностей определяется несколькими факторами: характером сравниваемых признаков (качественные или количественные), числом сопоставляемых групп, зависимостью или независимостью выборок, а также видом распределения признака.
Выборки являются независимыми, если набор объектов исследования в каждую из групп осуществлялся независимо от того, какие объекты исследования включены в другую группу. Так, в частности, происходит при рандомизации, когда распределение объектов происходит случайным образом. Примером сравнения независимых выборок может служить сопоставление данных анализа крови в группе пациентов с аналогичными показателями в группе здоровых.
Группы являются зависимыми (связанными) в динамических исследованиях, когда изучаются одни и те же объекты в разные моменты времени. Например, показатели анализа крови у одних и тех же пациентов до и после лечения.
От вида распределения и типа исследуемого признака зависит выбор подходящего математико-статистического критерия. Критерии делятся на два типа – параметрические и непараметрические.
Параметрические критерии – критерии, основанные на оценке параметров распределения, к которым относятся среднее арифметическое, среднеквадратическое отклонение, дисперсия. Они применимы только в том случае, если численные данные подчиняются нормальному распределению. Если распределение отличается от нормального, следует пользоваться так называемыми непараметрическими критериями.
Непараметрические критерии не основаны на оценке параметров распределения и вообще не требуют, чтобы данные подчинялись какому-то определенному типу распределения. Непараметрические критерии дают более грубые оценки, чем параметрические, но являются более универсальными. А параметрические методы более точны, но лишь в случае, если правильно определено распределение совокупности.
Перед тем как перейти к рассмотрению статистических критериев, введем понятия нулевой и альтернативной гипотез, которые нам потребуются в дальнейшем.
Нулевая гипотеза не может быть отвергнута, если ее вероятность окажется выше некого наперед заданного уровня α, достаточно близкого к 0, т.е. 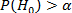
Альтернативная гипотеза 
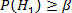
Поскольку 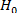

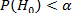
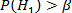
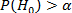
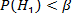
Например, в процессе исследования ставится задача доказать наличие статистически значимых различий между результатами наблюдений в опытной и контрольной группах, это значит что данные, полученные при применении того или иного статистического критерия должны позволить отвергнуть нулевую гипотезу об отсутствии указанных различий.
Параметрические критерии
Критерий Стьюдента (t-критерий) – критерий, основанный на сравнении средних значений выборок. Критерий Стьюдента является наиболее известным. С одной стороны, анализ средних значений сравнительно прост для вычислений. С другой стороны, средние величины наиболее наглядны и понятны.
Наиболее часто t-критерий используется в двух вариантах. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
Критерий Стьюдента для независимых выборок:
Рассмотрим выборку 
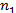
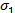
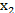
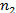


Нулевая гипотеза 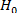



Альтернативная гипотеза 
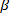
Проверка гипотез производится при помощи критерия Стьюдента, обозначаемого символом 
где 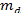

В случае независимых выборок критерий t рассчитывается следующим образом:
При этом как для первой, так и для второй выборки стандартная ошибка m рассчитывается по формуле:
Полученное значение критерия t сравнивают со стандартным табличным значением t-критерия Стьюдента 


Если 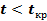
Если 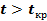
Имеется две группы пациентов, численностью 247 и 116 человек. Средний возраст пациентов первой группы наблюдения составил 32,06±9,62 лет (М±σ), средний возраст пациентов второй группы – 39,22±6,39 лет. Сравним 2 группы пациентов по возрасту при условии, что возраста в обеих группах были распределены нормально.
В начале рассчитаем стандартные ошибки для возрастов в каждой группе.
Поскольку t больше tкр =3, то нулевая гипотеза отвергается и различия между группами по возрасту можно считать статистически значимыми (р 2 (распределение Пирсона), поэтому для ее анализа критерий Стьюдента неприменим. Для того, чтобы приблизить распределение к нормальному рассматривают разность логарифмов сравниваемых дисперсий, которая обозначается символом Z:
Величина Z имеет нормальное распределение и, соответственно, к ней может быть применен критерий Стьюдента.
На практике часто рассматривают отношение F большей из сравниваемых дисперсий к меньшей (следуя свойствам логарифмов):
Полученная величина критерия сравнивается с критическим табличным значением. И также как в предыдущих рассуждениях, нулевая гипотеза либо отвергается и различие выборочных дисперсий считается статистически достоверным, либо делается вывод, что нулевую гипотезу отвергнуть нельзя и разница выборочных дисперсий находится в границах практически возможных случайных колебаний.
Если на независимых выборках была обнаружена достоверность различия дисперсий, то их средние значения нельзя сравнивать по t— критерию Стьюдента!
Рассмотренный метод сравнения мер вариации и его модификации являются основой чрезвычайно мощного и информативного метода математико-статистического анализа данных, получившего название дисперсионный анализ.
Параметрические критерии



Методы сравнительной статистики
Наиболее часто встречающейся и достаточно сложной математико-статистической задачей является сравнение данных, полученных в процессе наблюдений или экспериментов, в выборочных совокупностях. Исследователь старается описать результаты наблюдения количественными методами и «на выходе» получает числовой массив тех или иных доступных ему измерений – вариационный ряд.
Однако, как правило, содержащаяся в результатах измерений содержательная информация, имеет гораздо большую ценность при сравнении ее с аналогичной информацией, но полученной некоторым иным образом. Например, это может быть ситуация сравнения опытных данных (когда мы как-то повлияли на изучаемый объект или явление) с контрольной группой, в которой никакого воздействия на объект наблюдения не было. Возможно и сравнение двух вариантов опытов. Возможно сравнение двух серий наблюдений, разделенных в пространстве и времени и т.п.
Допустим, что удается заметить какие-либо численные различия в характеристиках сравниваемых рядов. Первым делом возникает вопрос: какова вероятность, что эти различия неслучайны и будут систематически повторяться в дальнейшем при воспроизведении условий эксперимента или наблюдения, т.е. выявленные различия являются статистически значимыми.
Выбор подходящего метода сравнения выборочных совокупностей определяется несколькими факторами: характером сравниваемых признаков (качественные или количественные), числом сопоставляемых групп, зависимостью или независимостью выборок, а также видом распределения признака.
Выборки являются независимыми, если набор объектов исследования в каждую из групп осуществлялся независимо от того, какие объекты исследования включены в другую группу. Так, в частности, происходит при рандомизации, когда распределение объектов происходит случайным образом. Примером сравнения независимых выборок может служить сопоставление данных анализа крови в группе пациентов с аналогичными показателями в группе здоровых.
Группы являются зависимыми (связанными) в динамических исследованиях, когда изучаются одни и те же объекты в разные моменты времени. Например, показатели анализа крови у одних и тех же пациентов до и после лечения.
От вида распределения и типа исследуемого признака зависит выбор подходящего математико-статистического критерия. Критерии делятся на два типа – параметрические и непараметрические.
Параметрические критерии – критерии, основанные на оценке параметров распределения, к которым относятся среднее арифметическое, среднеквадратическое отклонение, дисперсия. Они применимы только в том случае, если численные данные подчиняются нормальному распределению. Если распределение отличается от нормального, то следует пользоваться так называемыми непараметрическими критериями.
Непараметрические критерии не основаны на оценке параметров распределения и вообще не требуют, чтобы данные подчинялись какому-то определенному типу распределения. Непараметрические критерии дают более грубые оценки, чем параметрические, но являются более универсальными. А параметрические методы более точны, но лишь в случае, если правильно определено распределение совокупности.
Перед тем как перейти к рассмотрению статистических критериев, введем понятия нулевой и альтернативной гипотез, которые нам потребуются в дальнейшем.
На каждом шаге процесса анализа данных выдвигаются две гипотезы. Первая обозначается 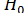
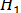
Нулевая гипотеза не может быть отвергнута, если ее вероятность окажется выше некого наперед заданного уровня α, достаточно близкого к 0, т.е. 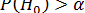
Альтернативная гипотеза 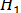
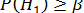
Поскольку 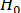
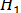
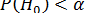
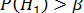
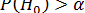
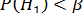
Например, в процессе исследования ставится задача доказать наличие статистически значимых различий между результатами наблюдений в опытной и контрольной группах. Это значит, что данные, полученные при применении того или иного статистического критерия, должны позволить отвергнуть нулевую гипотезу об отсутствии указанных различий.
Параметрические критерии
Заключение о случайности или неслучайности различий между выборочными совокупностями при использовании параметрических критериев осуществляется на основании сравнения параметров распределений, т.е. сводных числовых характеристик. Каждый из параметров компактно, в виде одного единственного числа, отражает некие характерные свойства распределения данной случайной величины. Они являются количественными мерами этих свойств. На практике, как правило, рассматривают лишь два параметра – среднее значение, являющееся «мерой положения математического центра» полученного вариационного ряда, и дисперсию, но чаще всего корень из нее – стандартное отклонение, являющиеся мерой вариации. Для этих параметров разработаны два наиболее популярных параметрических критерия: критерий Стьюдента и критерий Фишера.
Критерий Стьюдента (t-критерий) – критерий, основанный на сравнении средних значений выборок. Критерий Стьюдента является наиболее известным. С одной стороны, анализ средних значений сравнительно прост для вычислений. С другой стороны, средние величины наиболее наглядны и понятны.
Наиболее часто t-критерий используется в двух вариантах. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
Для того, чтобы определить, является ли нормальным исследуемое распределение, используются критерии Шапиро-Уилка и Колмогорова-Смирнова.
6.1 Параметрические критерии
В группу параметрических критериев методов математической статистики входят методы для вычисления описательных статистик, построения графиков на нормальность распределения, проверка гипотез о принадлежности двух выборок одной совокупности. Эти методы основываются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения. Среди параметрических критериев статистики нами будут рассмотрены критерий Стьюдента и Фишера.
6.1.1 Методы проверки выборки на нормальность
Чтобы определить, имеем ли мы дело с нормальным распределением, можно применять следующие методы:
1) в пределах осей можно нарисовать полигон частоты (эмпирическую функцию распределения) и кривую нормального распределения на основе данных исследования. Исследуя формы кривой нормального распределения и графика эмпирической функции распределения, можно выяснить те параметры, которыми последняя кривая отличается от первой;
2) вычисляется среднее, медиана и мода и на основе этого определяется отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.
3) эксцесс кривой распределения должен быть равен 0. Кривые с положительным эксцессом значительно вертикальнее кривой нормального распределения. Кривые с отрицательным эксцессом являются более покатистыми по сравнению с кривой нормального распределения;
4) после определения среднего значения распределения частоты и стандартного oтклонения находят следующие четыре интервала распределения сравнивают их с действительными данными ряда:
а) 
— к интервалу должно относиться около 50% частоты совокупности,
— к интервалу должно относиться около 75% частоты совокупности,
— к интервалу должно относиться около 100% частоты совокупности.
6.1.2 Критерий Стьюдента ( t-критерий)
Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».
При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанныхдвухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.
Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.
а) случай независимых выборок
Статистика критерия для случая несвязанных, независимых выборок равна:
— средние арифметические в экспериментальной и контрольной группах,
— стандартная ошибка разности средних арифметических. Находится из формулы:
где n 1 и n 2 соответственно величины первой и второй выборки.
Если n 1= n 2, то стандартная ошибка разности средних арифметических будет считаться по формуле:
где n величина выборки.
Подсчет числа степеней свободы осуществляется по формуле:
Далее необходимо сравнить полученное значение t эмп с теоретическим значением t—распределения Стьюдента (см. приложение к учебникам статистики). Если t эмп t крит, то гипотеза H 0 принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.
Пример 1. В двух группах учащихся — экспериментальной и контрольной — получены следующие результаты по учебному предмету (тестовые баллы; см. табл. 1).
Таблица 1. Результаты эксперимента
Первая группа (экспериментальная) N 1=11 человек
Вторая группа (контрольная)
12 14 13 16 11 9 13 15 15 18 14
13 9 11 10 7 6 8 10 11
Общее количество членов выборки: n 1=11, n 2=9.
Расчет средних арифметических: Хср=13,636; Y ср=9,444
Стандартное отклонение: s x=2,460; s y =2,186
По формуле (2) рассчитываем стандартную ошибку разности арифметических средних:
Считаем статистику критерия:
Сравниваем полученное в эксперименте значение t с табличным значением с учетом степеней свободы, равных по формуле (4) числу испытуемых минус два (18).
Табличное значение tкрит равняется 2,1 при допущении возможности риска сделать ошибочное суждение в пяти случаях из ста (уровень значимости=5 % или 0,05).
Если полученное в эксперименте эмпирическое значение t превышает табличное, то есть основания принять альтернативную гипотезу (H1) о том, что учащиеся экспериментальной группы показывают в среднем более высокий уровень знаний. В эксперименте t=3,981, табличное t=2,10, 3,981>2,10, откуда следует вывод о преимуществе экспериментального обучения.
Здесь могут возникнуть такие вопросы:
1. Что если полученное в опыте значение t окажется меньше табличного? Тогда надо принять нулевую гипотезу.
2. Доказано ли преимущество экспериментального метода? Не столько доказано, сколько показано, потому что с самого начала допускается риск ошибиться в пяти случаях из ста (р=0,05). Наш эксперимент мог быть одним из этих пяти случаев. Но 95% возможных случаев говорит в пользу альтернативной гипотезы, а это достаточно убедительный аргумент в статистическом доказательстве.
3. Что если в контрольной группе результаты окажутся выше, чем в экспериментальной? Поменяем, например, местами, сделав
средней арифметической экспериментальной группы, a
Отсюда следует вывод, что новый метод пока не проявил себя с хорошей стороны по разным, возможно, причинам. Поскольку абсолютное значение 3,9811>2,1, принимается вторая альтернативная гипотеза (Н2) о преимуществе традиционного метода.
б) случай связанных (парных) выборок
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:
Sd вычисляется по следующей формуле:
Если t эмп t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 2. Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест. Из методических соображений в таблице 2 приводятся результаты небольшого числа испытуемых.
Таблица 2. Результаты эксперимента
до начала эксперимента (Х)
Вначале произведем расчет по формуле:
Затем применим формулу (6), получим:
И, наконец, следует применить формулу (5). Получим:
Число степеней свободы: k =10-1=9 и по таблице Приложения 1 находим tкрит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтернативной гипотезы (H1) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.
6.1.3 F — критерий Фишера
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
— дисперсии первой и второй выборки соответственно.
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице.
Число степеней свободы определяется также просто:
В Приложении 1 критические значения критерия Фишера находятся по величинам k 1 (верхняя строчка таблицы) и k 2 (левый столбец таблицы).
Если t эмп> t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
Рассчитав дисперсии для переменных X и Y, получаем:
Тогда по формуле (8) для расчета по F критерию Фишера находим:
6.2 Непараметрические критерии
Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.
6.2.1 Критерий знаков ( G-критерий)
Критерий предназначен для сравнения состояния некоторого свойства у членов двух зависимых выборок на основе измерений, сделанных по шкале не ниже ранговой.
Нулевая гипотеза формулируются следующим образом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно различны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.
Статистика критерия (Т) определяется следующим образом:
Пример 4. Учащиеся выполняли контрольную работу, направленную на проверку усвоения некоторого понятия. Пятнадцати учащимся затем предложили электронное пособие, составленное с целью формирования данного понятия у учащихся с низким уровнем обучаемости. После изучения пособия учащиеся снова выполняли ту же контрольного работу, которая оценивалась по пятибалльной системе.
Результаты двукратного выполнения работы представляют измерения по шкале порядка (пятибалльная шкала). В этих условиях возможно применение знакового критерия для выявления тенденции изменения состояния знаний учащихся после изучения пособия, так как выполняются все допущения этого критерия.
Результаты двукратного выполнения работы (в баллах) 15 учащимися запишем в форме таблицы (см. табл. 1).