Что такое передача информации модель шеннона
Урок 2
Работа в локальной сети компьютерного класса в режиме обмена файлами
Содержание урока
Передача информации по техническим каналам связи
Передача информации по техническим каналам связи
Схема Шеннона
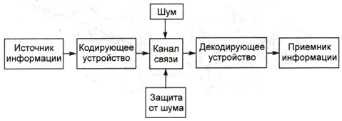
Американский ученый, один из основателей теории информации, Клод Шеннон предложил схему процесса передачи информации по техническим каналам связи (рис. 1.3).
Рис. 1.3. Схема технической системы передачи информации
Работу такой схемы можно пояснить на знакомом всем процессе разговора по телефону. Источник информации — говорящий человек. Кодирующее устройство — микрофон телефонной трубки, с помощью которого звуковые волны (речь) преобразуются в электрические сигналы. Канал связи — телефонная сеть (провода, коммутаторы телефонных узлов, через которые проходит сигнал). Декодирующее устройство — телефонная трубка (наушник) слушающего человека — приемника информации. Здесь пришедший электрический сигнал превращается в звук.
Здесь передача информации производится в форме непрерывного электрического сигнала. Это аналоговая связь.
Кодирование и декодирование информации
Под кодированием понимается любое преобразование информации, идущей от источника, в форму, пригодную для ее передачи по каналу связи.
На заре эры радиосвязи применялся код азбуки Морзе. Текст преобразовывался в последовательность точек и тире (коротких и длинных сигналов) и передавался в эфир. Принимавший на слух такую передачу человек должен был суметь декодировать код обратно в текст. Еще раньше азбука Морзе использовалась в телеграфной связи. Передача информации с помощью азбуки Морзе — пример дискретной связи.
В настоящее время широко используется цифровая связь, когда передаваемая информация кодируется в двоичную форму (0 и 1 — двоичные цифры), а затем декодируется в текст, изображение, звук. Цифровая связь, очевидно, тоже является дискретной.
Шум и защита от шума. Теория кодирования Шеннона
Информация по каналам связи передается посредством сигналов различной физической природы: электрических, электромагнитных, световых, акустических. Информационное содержание сигнала заключается в значении или в изменении значения его физической величины (силы тока, яркости света и пр.). Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи прежде всего возникают по техническим причинам: плохое качество линий связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Часто, беседуя по телефону, мы слышим шум, треск, мешающие понять собеседника, или на наш разговор накладывается разговор других людей. В таких случаях необходима защита от шума.
В первую очередь применяются технические способы защиты каналов связи от воздействия шумов. Такие способы бывают самыми разными, иногда простыми, иногда очень сложными. Например, использование экранированного кабеля вместо «голого» провода; применение разного рода фильтров, отделяющих полезный сигнал от шума, и пр.
К. Шеннон разработал специальную теорию кодирования, дающую методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования Шеннона как раз и позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи часто применяется следующий прием борьбы с потерей информации при передаче. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета, и если она не совпадает с первоначальной, то передача данного пакета повторяется. Так происходит до тех пор, пока исходная и конечная контрольные суммы не совпадут.
Коротко о главном
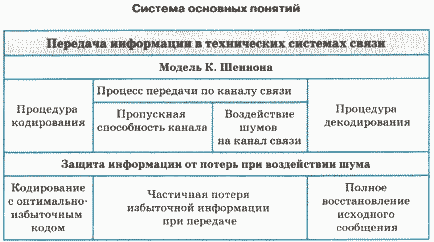
Любая техническая система передачи информации состоит из источника, приемника, устройств кодирования и декодирования и канала связи.
Под кодированием понимается преобразование информации, идущей от источника, в форму, пригодную для ее передачи по каналу связи. Декодирование — это обратное преобразование.
Шум — это помехи, приводящие к потере информации.
В теории кодирования разработаны методы представления передаваемой информации с целью уменьшения ее потерь под воздействием шума.
Вопросы и задания
1. Назовите основные элементы схемы передачи информации, предложенной К. Шенноном.
2. Что такое кодирование и декодирование при передаче информации?
3. Что такое шум? Каковы его последствия при передаче информации?
4. Какие существуют способы борьбы с шумом?
ЕК ЦОР: Часть 2, заключение, дополнение к главе 1, § 1.1. ЦОР № 1.
Модель связи Шеннона (перевод Great Principles of Computing)
В 1948 году Шеннон в своей «теории связи» предложил математическую модель связи. Её смысл в следующем.
Есть источник и есть приёмник. Источник отправляет сообщения, а приёмник принимает. Оба участника пользуются одинаковым словарем для кодирования и раскодирования сообщений.
Модель Шеннона применима к любой системе, которая кодирует, раскодирует, передает, хранит и получает сообщения. Так можно рассматривать природу как источник физических законов (сообщений), а процесс открытия этих законов — как канал связи (Dretske 1981).
Шум еще одна составляющая этой модели. Шум — то, что заставляет приёмник неверно истолковывать сообщения. Плохая видимость (туман и сумерки) нарушает семафорное сообщение между судами; вспышки молнии прерывают передачу радиоволн AM-частот; царапины на CD могут сделать его нечитаемым; множество посторонних шумов делают речь неразборчивой.
Стоит заметить, что кодирование в системах связи — не то же, что и шифрование секретных сообщений. Шифрование предполагает существование специального ключа: получить исходный текст сможет только тот, у кого есть этот ключ.
В своей модели Шеннон в качестве «словаря для кодирования» выбрал биты. Он утверждал, что любое сообщение может быть представлено в виде набора бит, т.e. в прямом смысле оцифровано, любая информация превращает в цифры, в набор нулей и единиц.
Любопытно посмотреть на то, как оцифровывать сообщения и что такое шум, на упрощенном примере.
Пусть источник может передавать только сообщения состоящие из 4 букв: A, B, C и D. Используем двухбитовые коды для обозначения этих букв:
A: 11
B: 10
C: 01
D: 00
Например, источник хочет сказать: «CAB». Этому сообщению соответствует код «011110». Источник отправляет этот набор бит в канал, а приёмник их получает и запускает обратный процесс: разбивает код на пары бит и сверяет со словарем.
Возникает вопрос: достаточно ли двух бит для кодирования этих букв? Естественно, что чем меньше бит требуется для этой цели — тем лучше: сообщения занимают меньше места, передаются быстрее. Однако, короткий код намного проще испортить, внеся даже небольшие искажения, которые привносит шум.
Например, если первый бит в букве A по каким-то причинам потеряется, мы получим 010110 — что соответствует CCB, а это полностью меняет смысл сообщения. Как быть?
Добавим дополнительный бит для каждой буквы (бит четности):
A: 110
B: 101
C: 011
D: 000
Теперь, если первый бит в A теряется мы получаем 010 — такой тройки в словаре нет, поэтому приемник легко может понять, что это ошибка. Однако, он не сможет восстановить исходное сообщение.
Если добавить еще несколько лишних битов, то это поможет приемнику не только выяснить где ошибка, но и восстановить исходный код:
A: 11111
B: 10010
C: 01001
D: 00100
Каждый код отличает от другого как минимум на 3 бита. Теперь испорченный бит показывает набор, который по-прежнему отличается от верного на один бит, но теперь он отличается на два или более битов от всех остальных в словаре! Соответственно, приёмник может легко «поправить» испорченное сообщение.
Инжерен связи Ричард Хемминг (Richard Hamming) впервые сформулировал правило, по которому можно определить достаточное «расстояние» между наборами бит. По Хеммингу, расстояние — это количество бит на которые отличаются наборы бит друг от друга. Теперь эта величина называется расстоянием Хемминга.
Хемминг понял, что для того, чтобы поправить k ошибок, достаточно чтобы расстояние Хемминга было равно 2^k — 1. Хемминг так же разработал семейство кодов (коды Хемминга), которые получаются добавлением битов четности к исходным кодам и создал схемы, которые позволяют легко получать исходные сообщения (с учетом исправления ошибок). Коды Хемминга широко используются при передаче сообщений от процессора к памяти компьютера.
Коды Хемминга хорошо работают, когда шум распределен случайным образом. Однако, в некоторых сигналах шум возникает периодически или на относительно длительное время. С этой задачей хорошо справляются другой тип кодов — коды Рида-Соломона (Reed-Solomon). С точки зрения математики, они более хитрые, однако и те и другие легко могут быть выполнены на интегральных схемах компьютера.
Теорема Шеннона и передача информации.
Основное значение результатов Шеннона в этой области состоит в том, что они дают универсальный критерий, позволяющий сравнивать технически различные устройства и системы с точки зрения их возможностей по передаче информации. Технически источники сообщений и каналы связи могут быть существенно разными устройствами по используемым сигналам, способам кодирования сообщений, форматам данных, скоростным характеристикам. В этих условиях информационная мера Шеннона и теоремы идеального кодирования позволяют оценить, в какой степени технически различные системы соответствуют друг другу для решения задачи передачи сообщений. Для этого требуется, исходя из технических показателей источника и канала, оценить их информационные показатели: информационную производительность и информационную пропускную способность. Соотношение информационных показателей и является той идеальной мерой, по которой можно судить о степени соответствия реальных систем.
Особая заслуга Шеннона состоит в том, что он первым осознал действительную картину влияния случайных помех на процесс передачи сообщений. Принципиальное действие помех выражается в той степени, в какой они влияют на информационные показатели системы. Поэтому каналы с одинаковой пропускной способностью эквивалентны по возможности безошибочной передачи сообщений не зависимо от того, действуют ли в них помехи или нет.
Для наглядного пояснения роли теоремы Шеннона прибегнем к следующему сравнению. Пусть имеется трубопровод для доставки от источника некоторого жидкого продукта. Технические возможности трубопровода определяются количеством жидкости, которое можно передать по нему в единицу времени. Производительность источника определим количеством чистого продукта, поступающего от него в единицу времени, а пропускную способность трубопровода — как максимально возможную скорость передачи чистого продукта, соответствующую условию, что от источника поступает чистый продукт без примесей. Аналогом канала с помехами может служить трубопровод с утечкой. Пропускная его способность будет меньше. Чем в трубопроводе без утечки, на величину утечки продукта за единицу времени. Можно теперь представить, какой эффект вызвало бы утверждение, что существует такой способ введения примеси («избыточности») в продукт, при котором, введя количество примеси, равное утечке в трубопроводе, можно по нему доставлять продукт без потерь со скоростью, отвечающей пропускной способности трубопровода с утечкой. Именно такой смысл имеет теорема Шеннона применительно к задаче передачи информации. Продолжая аналогию этого примера, можно сказать, что такой способ введения примеси требует наличия некоего «отстойника», в котором примесь будет отстаиваться в течении определенного времени перед подачей в трубопровод (в идеале — бесконечное время). После такого «отстоя» при движении жидкости по трубопроводув утечку будет уходить только примесь.
Интерпретация результатов Шеннона для задач хранения и поиска информации. Результаты теорем Шеннона, традиционно формулируемые для задачи передачи сообщений, легко распространяются на задачи хранения и поиска информации.
Рассмотрим задачу хранения данных в следующей обобщенной форме. Пусть данные в виде последовательности записей размещаются в ячейках запоминающего устройства (ЗУ); каждая запись помещается в отдельную ячейку. Записи, предназначенные для хранения, характеризуются некоторой совокупностью технических особенностей: размерами, способами кодирования данных, форматами кодов и т.п. Ячейки ЗУ, в которых размещаются записи, также характеризуются некоторой совокупностью своих технических особенностей: внутренним представлением данных, способом доступа, системой меток и рядом технических ограничений на процесс размещения данных. Кроме того, информация, размещаемая в ячейках ЗУ, может подвергаться воздействию помех, из-за чего в записях появляются ошибки.
Возникает вопрос, при каких условиях возможно достоверное хранение информации, т.е. получение из ЗУ данных в том виде, в каком они были туда помещены.
Для ответа на этот вопрос в соответствии с шенноновским подходом необходимо перейти от технических характеристик к информационным:
— для запоминаемых данных определить среднюю энтропию записи;
— для ЗУ определить максимальное количество информации, которое может быть размещено в ячейке с учетом ее технических ограничений и действующих в ней помех, то есть определить информационную емкость ячейки.
Тогда для информационных пользователей будет справедлива следующая формулировка теоремы Шеннона для задачи хранения информации: для запоминающего устройства (с помехами и без помех) существует способ сколь угодно достоверного кодирования и декодирования хранимых данных, если только средняя энтропия записи меньше информационной емкости ячейки.
Если рассмотреть применение идеального кодирования к задаче хранения информации, то станет ясно, что для этого потребуется ЗУ с потенциально бесконечным числом ячеек, чтобы разместить в нем типичные последовательности записей сколь угодно большой длины. В этом проявляется техническая нереализуемость идеального кодирования применительно к задаче хранения информации.
К идеальному результату можно приблизиться, укрупняя хранимые записи. На практике в устройствах хранения данных для ЭВМ (например, в накопителях на магнитных лентах и дисках) широко применятся так называемое блокирование записей. При этом группы записей объединяются в блоки, которые размещаются в ЗУ как некоторые единые укрупненные записи. Этим достигается более экономное использование информационной емкости ячеек.
Практическая реализация помехоустойчивого хранения информации основана на методах помехоустойчивого кодирования. Перед помещением записей в ЗУ искусственно увеличивается их избыточность за счет введения дополнительных контрольных символов. После считывания записей из ЗУ производится обнаружение и коррекция ошибок.
Рассмотрим теперь задачу поиска в следующей обобщенной форме. Пусть имеется файл, записи которого идентифицируются ключами. Множество запросов записей образуют последовательность аргументов поиска. Знания ключей и аргументов поиска могут подвергаться искажением из-за действия случайных помех при формировании файла и при подготовке запросов.
Возникает вопрос, при каких условиях возможен достоверный поиск информации, т.е. получение на каждый запрос именно тех записей которые требуются.
В соответствии с шенноновским подходом перейдем к информационным характеристикам:
— для последовательностей аргументов поиска определим среднюю энтропию аргументов. Если на аргументы действуют ошибки, то необходимо учесть увеличение средней энтропии вследствие ошибок;
— для множества записей файла определим информационную емкость ключа — максимальное количество информации, которое может содержаться в ключе файла. Если ключи файла могут содержать случайные ошибки, то необходимо учесть уменьшение информационной емкости ключа вследствие ошибок.
Тогда для информационных показателей будет справедлива следующая формулировка теоремы Шеннонадля задачи поиска информации:
Для поиска в файле (с помехами и без помех) существует способ сколь угодно достоверного поиска нужных записей, если только средняя энтропия аргумента меньше информационной емкости ключа.
Применение алгоритма идеального кодирования в данной задаче потребует потенциально бесконечного укрупнения файла, чтобы производить поиск в качестве аргумента выступают типичные последовательности исходных аргументов. В этом проявляется техническая нереализуемость идеального кодирования применительно к задаче поиска информации.
Как упоминалось во второй главе, разработка технически реализуемых способов помехоустойчивого поиска в настоящее время находится в зачаточном состоянии своего развития. Имеющиеся здесь результаты существенно скромнее, чем, например, в помехоустойчивом кодировании, где создана обширная и глубокая математическая теория кодирования. В чем здесь дело? Почему бы не воспользоваться результатами теории кодирования для решения родственной задачи поиска.
Основная идея помехоустойчивого кодирования состоит в искусственном введении избыточности в сообщения по подачи их в канал с помехами. В большинстве задач поиска мы имеем дело с естественной избыточностью сообщений, на которую мы не можем активно воздействовать. Мы получаем уже искаженный аргумент поиска, например, невнятно произнесенную по телефону фамилию клиента, и можем рассчитывать только на естественную избыточность языка (естественная избыточность русского языка, как и большинства европейских языков, оставляет примерно 60 % ).
Однако, учитывая принципиальную разрешимость этой задачи в свете результатов Шеннона, а также последние публикации по проблемам помехоустойчивого поиска можно надеяться, что эта проблема будет решена и технически.
Сжатие данных.
Закодированные сообщения передаются по каналам связи, хранятся в запоминающих устройствах, обрабатываются процессором. Объемы данных, циркулирующих в АСУ, велики, и поэтому в о многих случаях важно обеспечить такое кодирование данных, которое характеризуется минимальной длиной получающихся сообщений. Эта проблема сжатия данных. Решение её обеспечивает увеличение скорости передачи информации и уменьшение требуемой памяти запоминающих устройств. В конечном итоге это ведет к повышению эффективности системы обработки данных.
Существует два подхода (или два этапа) сжатия данных:
— сжатие, основанное на анализе конкретной структуры и смыслового содержания данных;
— сжатие, основанное на анализе статистических свойств кодируемых сообщений. В отличие от первого второй подход носит универсальный характер и может использоваться во всех ситуациях, где есть основания полагать, что сообщения подчиняются вероятностным законам. Далее мы рассмотрим оба этих подхода.
4.1. Сжатие на основе смыслового содержания данных
Эти методы носят эвристический, уникальный характер, однако основную идею можно пояснить следующим образом. Пусть множество содержит элементов. Тогда для кодирования элементов множества равномерным кодом потребуется двоичных знаков. При этом будут использованы все двоичные кодовые комбинации. Если используются не все комбинации, код будет избыточным. Таким образом, для сокращения избыточности следует попытаться очертить множество возможных значений элементов данных и с учетом этого произвести кодирование. В реальных условиях это не всегда просто, некоторые виды данных имеют очень большую мощность множества возможных значений. Посмотрим, как же поступают в конкретных случаях.
Переход от естественных обозначений к более компактным. Значения многих конкретных данных кодируются в виде, удобном для чтения человеком. При этом они содержат обычно больше символов, чем это необходимо. Например, дата записывается в виде «26 января 1982 г.» или в самой краткой форме: «26.01.82». при этом многие кодовые комбинации, например «33.18.53» или «95.00.11», никогда не используются. Для сжатия таких данных день можно закодировать пятью разрядами, месяц — четырьмя, год — семью, т.е. вся дата займет не более двух байтов. Другой способ записи даты, предложенный еще в средние века состоит в том, чтобы записывать общее число дней, прошедших к настоящему времени с некоторой точки отсчета. При этом часто ограничиваются четырьмя последними цифрами этого представления. Например, 24 мая 1967 года записывается в виде 0000 и отсчет дней от этой даты требует, очевидно, два байта в упакованном десятичном формате.
Дата добавления: 2016-03-22 ; просмотров: 937 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Урок 13
Хранение и передача информации (§§ 7, 8)
Содержание урока
Передача информации
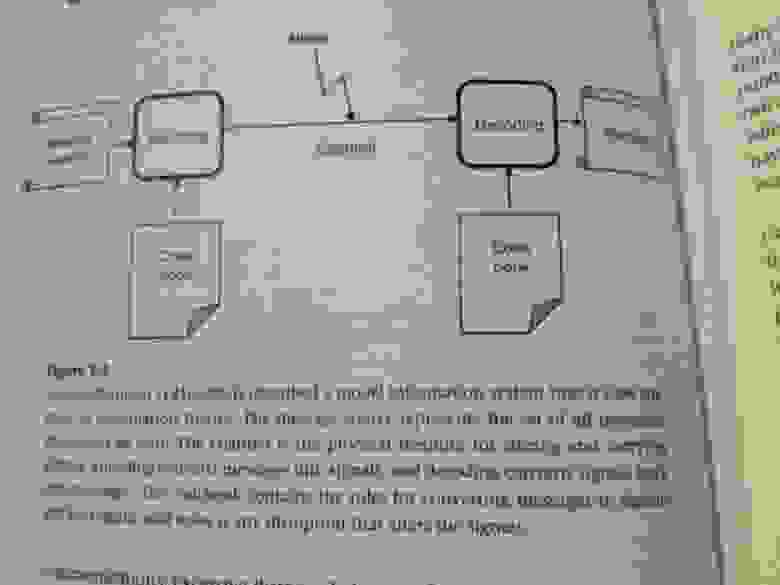




 Из курса основной школы вам известно:
Из курса основной школы вам известно: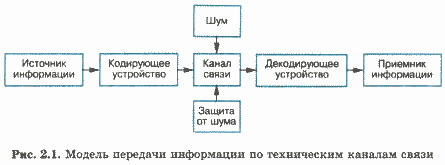
 Однако существует другая проблема, которая на рис. 2.1 отмечена словом «шум».
Однако существует другая проблема, которая на рис. 2.1 отмечена словом «шум».
 Хранение и передача информации (§§ 7, 8)
Хранение и передача информации (§§ 7, 8)