Что такое переключательная функция
Переключательные функции
Любое логическое выражение, составленное из n переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. Двоичная функция может принимать только два значения: 0 и 1 – в зависимости от значений переменных. Такие функции являются удобным инструментом для описания, анализа и синтеза переключательных схем (бесконтактных и контактных), поэтому они называются переключательными функциями (ПФ).
Существуют несколько способов задания ПФ.
1. Табличный, когда функция задается в виде таблицы истинности (соответствия). Таблица истинности содержит 2 n строк ( по числу наборов), n столбцов значений аргументов и один столбец значений функции. В таблице каждому набору аргументов соответствует значение функции.
Таблица истинности ПФ, значения которой соответствуют значениям, принимаемым большинством переменных в наборе (функция голосования), определяет ПФ мажоритарного элемента “два из трех” (переноса двоичного разряда.
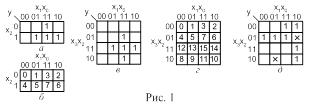
На рис. 1,а приведена карта Карно для ПФ мажоритарного элемента “два из трех”, заданной таблицей истинности 2, на рис.1,в – для ПФ компаратора. На рис.1,б,г в клетках проставлены их номера, соответствующие номерам наборов.
Карты Карно являются важным средством проектирования логических схем. Особенность карт в том, что любые две соседние клетки отличаются значением какой-либо одной и только одной переменной. Эта особенность характеризует также клетки первой и последней строк, первого и последнего столбцов, поэтому такие клетки тоже можно считать соседними. Указанная особенность соседних клеток позволяет легко осуществлять упрощение ПФ посредством использования тождества склеивания.
Можно использовать для задания функции десятичные номера наборов, на которых функция принимает значение 0. Та же ПФ (рис.1,а) в таком случае будет задана как y( x2,x1,x0 ) = 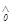
4. Аналитический способ, когда ПФ задается в виде алгебраического выражения (структурной формулы), получаемого путем применения логических операций к аргументам ПФ. Следует учитывать, что одну и ту же ПФ можно задать в виде разных структурных формул, которые отличаются друг от друга выбором используемых логических операций и своей сложностью.
При использовании всех n аргументов для записи алгебраического выражения существует две формы структурных формул.
Совершенная дизъюнктивная нормальная форма (СДНФ) представляет собой дизъюнкцию минтермов.
Пример: СДНФ для ПФ мажоритарного элемента (рис.1,а)
y= m3 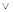
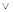
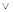
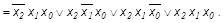
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой конъюнкцию макстермов.
Пример: СКНФ для ПФ мажоритарного элемента (рис.1,а)
y =M0M1M2M4 =( 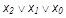
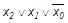
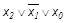
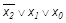
Минтермы (макстермы) называются соседними, если они отличаются формой представления только одной переменной (без инверсии, с инверсией). В примере (1) минтерм m7 является соседним по отношению ко всем остальным (m3, m5, m6). В примере (2) макстерм М0 является соседним по отношению ко всем остальным (М1,М2,М4).Признак соседства минтермов (макстермов) используется при применении закона склеивания (при минимизации ПФ с применением карт Карно).
Определение “совершенная форма” означает, что все минтермы или макстермы имеют одинаковую размерность (ранг), равную числу переменных n, от которых зависит ПФ.
Определение “нормальная форма” означает, что порядок логического уравнения не более двух. Порядок логического уравнения – количество последовательно выполняемых базовых операций алгебры логики при вычислении значения функции (операция инверсии в расчет не принимается). При реализации логических схем порядок ПФ определяет число каскадов логического преобразования входных переменных, необходимых для получения функции.
Можно привести и более простые алгебраические выражения для ПФ мажоритарного элемента (рис.1,а):
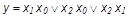
y = ( 
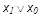
Переключательные функции. Булева алгебра



Алгебра, заданная на булевом носителе, называется булевой алгеброй или алгеброй логики.
Опр: Переключательная функция f(x1,x2,…,xn)— это функция, принимающая значения из множества В, аргументы которой тоже принимают значения 0 или 1.
Пример:голосование 3 человек.
| I | |
| II | |
| III | |
| итог | |
| Нулевое множество (состоит из нулевых наборов) | Единичное множество (состоит из единичных наборов) |
0 0 0 1 1 f2 =х – тождественная;

Опр: Переменная xi в функции f(x1,… xi …xn) называется фиктивной (несущественной), если от нее не зависит значение функции:
В этом случае значение функция n переменных зависит от n-1 переменной, т.е. фиктивную переменную можно удалить из задания функции.
Остальные переменные называются существенными.
С использованием добавления фиктивных переменных можно все функции рассматривать как функции от одного количества переменных.
Способы задания функций:
1. Таблица истинности
Список переменных | Значения функции
Используемые функции от двух переменных:

0 0 1 0 0 1 0 1 1 0
0 1 0 1 0 1 0 0 1 1
1 0 0 1 0 0 1 0 1 1
1 1 1 1 1 1 0 0 0 0
Функции описываются с использованием операторов:
Основной задачей теории булевых функций является разработка методов построения сложных функций из более простых композицией. Описание формулой композиции функций называется суперпозицией.
Переменные в формуле имеют глубину 0, сама формула имеет высшую глубину. Разбиение формулы по глубинам облегчает вычисление значения функции.
Пример:F=(у or x) xor (x and (x xor y))
После построения таблицы истинности имеем F=y, при этом х- фиктивная переменная.
Две формулы эквивалентны (равносильны), если они описывают одну и ту же функцию, при упрощении их результаты совпадают, а значения функций в таблице истинности при одних и тех же наборах равны. Если значение этой функции единично, то формула тождественно истинна, если значение функции нулевое, то формула тождественно ложна.
Для упрощения формул применяются свойства логических функций:
Основные свойства булевых функций:
1) идемпотентность: хÚх=х, хÙх=х,
2) коммутативность: хÙу=уÙх, хÚу=уÚх,
3) ассоциативность: хÚ(yÚz)= (хÚy)Úz, хÙ(yÙz)= (хÙy)Ùz,
4) поглощение: (xÙy)Úx=x, (xÚy)Ùx=x,
5) дистрибутивность: хÙ(yÚz)= (хÙy)Ú (хÙz), хÚ(yÙz)= (хÚy)Ù (хÚz),
6) 
7) 
8) 
9) действия с константами: xÚ0=x xÙ0=0

Приоритет: инверсия, конъюнкция, дизъюнкция, остальные функции.
Поскольку свойства определены только для И, ИЛИ, НЕ, то запишем некоторые подстановки (равносильные формулы):
Переключательные функции одного и двух аргументов
Переключательные функции одного аргумента. Переключательные функции двух аргументов. Представление переключательной функции в виде многочленов. Совершенная дизъюнктивная нормальная форма переключательной функции. Функция в виде полинома Жегалкина.
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
«Переключательные функции одного и двух аргументов»
1.Переключательные функции одного аргумента.
Существует четыре переключательные функции одного аргумента, которые приведены в табл. 1.
Переключательные функции одного аргумента
Функция f0(x) тождественно равна нулю. Она называется константой нуль и обозначается f0(x)=0.
Функция f1(x) повторяет значения аргумента и поэтому тождественно равна переменной x.
Функция f3(x) тождественно равна единице. Она называется константой единица и обозначается f3(x)=1.
2. Переключательные функции двух аргументов.
Существует шестнадцать различных переключательных функций двух аргументов, каждая из которых определена на четырех наборах. Эти функции представлены в табл. 2.
В число шестнадцати переключательных функций входят функции, рассмотренные в п.1:
Переключательные функции двух аргументов
Функция запрета по y
Функция запрета по x
Сумма по модулю 2 (логическая неравнозначность)
Логическое сложение (дизъюнкция)
Операция Пирса (стрелка Пирса)
Эквивалентность (логическая равнозначность)
Импликация от y к x
Импликация от x к y
Операция Шеффера (штрих Шеффера)
Рассмотрим некоторые переключательные функции двух аргументов.
Функция f1(x,y) называется конъюнкцией, или логическим умножением. Таблица истинности этой функции совпадает с таблицей умножения двух одноразрядных двоичных чисел. Можно ввести функцию n аргументов, соответствующую произведению n одноразрядных двоичных чисел. Такая переключательная функция равна единице тогда и только тогда, когда все ее аргументы равны единице. Для конъюнкции справедливы следующие соотношения:
Функция f7(x,y) называется дизъюнкцией или логическим сложением. Эта функция равна нулю только в том случае, когда все ее аргументы равны нулю. Можно ввести функцию n аргументов, соответствующую логическому сложению n одноразрядных двоичных чисел. Такая переключательная функция равна нулю тогда и только тогда, когда все ее аргументы равны нулю. Для конъюнкции справедливы следующие соотношения:
Таблица истинности функции f6(x,y) совпадает с таблицей сложения двух одноразрядных двоичных чисел по модулю два. Можно ввести функцию n аргументов, соответствующую сумме по модулю два n одноразрядных двоичных чисел. Такая переключательная функция определяется следующим условием: она равна единице, если число аргументов, равных единице, нечетно, и равна нулю, если число таких аргументов четно. Приведем некоторые соотношения для суммы по модулю два:
Рассмотренные шестнадцать функций двух аргументов (будем называть их элементарными) позволяют строить новые переключательные функции следующим образом:
путем перенумерации аргументов;
путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f1, f2, …, fk путем применения (возможно многократного) этих двух правил, будем называть суперпозицией функций f1, f2, …, fk. Например, имея элементарные функции инверсии, конъюнкции, дизъюнкции, импликации, запрета, сложения по модулю два, можно составить новую переключательную функцию:
Используя таблицы, определяющие элементарные функции, можно задавать в виде таблицы любую переключательную функцию, являющуюся суперпозицией этих функций.
Пример 1. Представить в виде таблицы функцию
Решение. Функцию f (x,y,z) будем представлять последовательно, записывая в столбцы табл. 1.5 промежуточные результаты, получаемые после выполнения каждой операции:
3. Представление переключательной функции в виде многочленов.
Рассмотрим переключательные функции, называемые конституентами.
Определение 1. Конституентой единицы называют переключательную функцию n аргументов, которая принимает значение, равное единице на одном единственном наборе аргументов.
Конституента единицы может быть выражена через конъюнкцию всех аргументов, каждый из которых входит в произведение со знаком отрицания или без него. Приведенную выше конституенту единицы можно представить через конъюнкцию аргументов следующим образом:
Пример 2. Записать конституенту, равную единице на двенадцатом наборе для функции пяти переменных.
Решение. Пятиразрядное двоичное число, равное двенадцати, записывается в виде: 01100. Запишем произведение пяти аргументов, располагая их в порядке возрастания индексов: x1 x2 x3 x4 x5. Сопоставляя это произведение с двоичным числом 01100, определяем, что знаки отрицания необходимо поставить над первым, четвертым и пятым аргументами:
Определение 3. Конституентой нуля называют переключательную функцию n аргументов, которая принимает значение, равное нулю, на одном единственном наборе аргументов.
Пример 3. Записать конституенту нуля, равную нулю на двадцать пятом наборе для функции пяти переменных.
Решение. Пятиразрядное двоичное число, равное двадцати пяти, записывается в виде: 11001. Запишем дизъюнкцию пяти аргументов, располагая их в порядке возрастания индексов: x1 x2 x3 x4 x5. Сопоставляя это произведение с двоичным числом 11001, определяем, что знаки отрицания необходимо поставить над первым, вторым и пятым аргументами:
2. Представление переключательной функции в виде полинома Жегалкина.
Теорема Жегалкина. Любая переключательная функ-ция может быть представлена в виде полинома (много-члена), т. е. записана в форме
—операция сложения по модулю два.
При записи конкретной переключательной функции в виде многочлена коэффициенты a0, a1x1, … aN выпа-дают, так как члены, при которых коэффициенты рав-ны нулю, можно опустить, а коэффициенты, равные еди-нице, не писать.
Действительно, на каждом из наборов с номерами m1, … mp равна единице только одна конституента, стоящая в правой части выражения (2), а осталь-ные равны нулю. Следовательно, на этих наборах и только на них правая часть выражения (2) принимает значение, равное единице.
Для того чтобы перейти от выражения (2) к виду (1), достаточно представить конституенты едини-цы в виде произведений и, используя соотношение , заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть на-пример, конституента единицы записана в виде
Раскрывая скобки и приводя подобные члены в соответствии со свойствами операции сложения по модулю два, получаем запись заданной функ-ции в форме (1), что и доказывает теорему.
Приведенное доказательство теоремы позволяет сформулировать правило представления любой пере-ключательной функции в виде многочлена.
Функция f58(x1,x2,x3) равна единице на втором, третьем, четвертом и шестом наборах, и может быть записана в виде суммы соответствующих конституент единицы:
Приводя подобные члены, окончательно находим
3. Совершенная дизъюнктивная нормальная форма переключательной функции.
Если подставить в выражение (3) значения f(i), то получим дизъюнкцию конституент, которые равны еди-нице на тех же наборах, что и заданная функция. Дей-ствительно, ввиду того, что 0x=0 и 0х=х, члены вы-ражения (2), в которых коэффициенты f(i)=0, можно опустить, а так как x 1 = x, то коэффициенты f(i)=1 можно не писать. Тогда
Определение 3. Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется совершенной дизъюнктивной нормальной формой переключательной функции.
Совершенную дизъюнктивную нормаль-ную форму переключательной функции удобно находить в такой последователь-ности:
выписать ряд произведений всех аргументов и соединить их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;
записать под каждым произведением набор аргу-ментов, на котором функция равна единице, и над аргу-ментами, равными нулю, поставить знаки отрицания.
Это правило называют иногда правилом запи-си переключательной функции по единицам.
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные единице, на следующих наборах аргументов:
0001, 0011, 0100, 0101, 1000, 1001, 1010, 1011, 1100, 1101, 1111.
Таким образом, совершенная дизъюнктивная нормальная форма функции f23805(x1,x2,x3,x4) будет состоять из одиннадцати дизъюнкций, каждая из которых представляет собой конъюнкцию четырех элементов:
4. Совершенная конъюнктивная нормальная форма переключательной функции.
Ввиду справедливости соотношений 1 x = 1 и 0 х= х, при подстановке в выражение (4) значений функ-ции f(i), сомножители, у которых f(i), == 1, можно опустить, а значения функции f(i)=0 не писать. Тогда
Определение 4. Произведение конституент нуля, которые равны нулю на тех же наборах, что и заданная функция, называется совершенной конъюнктивной нормальной формой.
Сформулируем правило представления переключа-тельной функции в совершенной конъюнктивной нор-мальной форме. Чтобы представить переключательную функцию п аргументов в совершенной конъюнктивной нормальной форме, достаточно:
выписать произведение дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;
выписать под каждым сомножителем набор аргу-ментов, на котором функция равна нулю, и над аргу-ментами, равными единице, поставить знаки отрицания;
Это правило иногда называют правилом запи-си переключательной функции по нулям.
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные нулю, на следующих наборах аргументов:
0000, 0010, 0110, 0111, 1110.
Таким образом, совершенная конъюнктивная нормальная форма функции f23805(x1,x2,x3,x4) будет состоять из пяти конъюнкций, каждая из которых представляет собой дизъюнкцию четырех элементов:
1. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.- М.: изд-во МГТУ им. Н.Э. Баумана, 2001.- 744 с. (Сер. Математика в техническом университете; Вып XIX).
2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.- М.: Наука, Физматлит, 2000.- 544 с.- ISBN 5-02-015238-2.
3. Зарубин В.С. Математическое моделирование в технике: Учеб. для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.- М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.- 496 с. (Сер. Математика в техническом университете; вып. XXI, заключительный).
Подобные документы
Отражение посредством математической функции связи между какими-либо значениями. Представление числовых функций на рисунках в виде графиков. Особенности алгебраической функции и многочленов. Практическое применение линейных и квадратических функций.
презентация [251,3 K], добавлен 07.10.2014
Введение в анализ и дифференциальное исчисление функции одного переменного. Нахождение локальных экстремумов функции. Интегральное исчисление функции, пределы интегрирования. Практический пример определения площади плоской фигуры, ограниченной кривыми.
контрольная работа [950,4 K], добавлен 20.01.2014
Понятие мероморфной функции и ее основные свойства. Характеристика теоремы Миттаг-Леффлера. Общий вид мероморфной функции с заданными полюсами, ее представление в виде суммы целой функции и ряда рациональных функций. Разбор случая простых полюсов.
курсовая работа [357,6 K], добавлен 20.07.2015
Алгоритм построения многочлена Жегалкина по совершенной дизъюнктивной нормальной форме. Диаграмма Эйлера-Венна, изображение универсального множества и подмножества. Проверка самодвойственности, монотонности и линейности логической функции двух переменных.
контрольная работа [227,5 K], добавлен 20.04.2015
контрольная работа [295,5 K], добавлен 24.03.2009
Основные аксиомы и тождества алгебры логики. Аналитическая форма представления булевых функций. Элементарные функции алгебры логики. Функции алгебры логики одного аргумента и формы ее реализации. Свойства, особенности и виды логических операций.
реферат [63,3 K], добавлен 06.12.2010
Нахождение частной производной первого порядка. Определение области определения функции. Расчет производной от функции, заданной неявно. Полный дифференциал функции двух переменных. Исследование функции на экстремум, ее наименьшее и наибольшее значения.
контрольная работа [1,1 M], добавлен 12.11.2014
Нахождение асимптот функции, локальных и глобальных экстремумов. Промежутки выпуклости и точки перегиба функции. Область определения функции и точки пересечения с осями. Нахождение определенного и неопределенного интегралов. Выполнение деления с остатком.
контрольная работа [312,9 K], добавлен 26.02.2012
Нахождение частных производных по направлению вектора. Составление уравнения касательной плоскости к поверхности в заданной точке. Исследование на экстремум функции двух переменных. Определение условного максимума функции при помощи функции Лагранжа.
контрольная работа [61,5 K], добавлен 14.01.2015
Понятие функции нескольких переменных. Аргументы, частное значение и область применения функции. Рассмотрение функции двух и трех переменных. Предел функции нескольких переменных, теорема. Главная сущность непрерывности функции нескольких переменных.
реферат [86,3 K], добавлен 30.10.2010