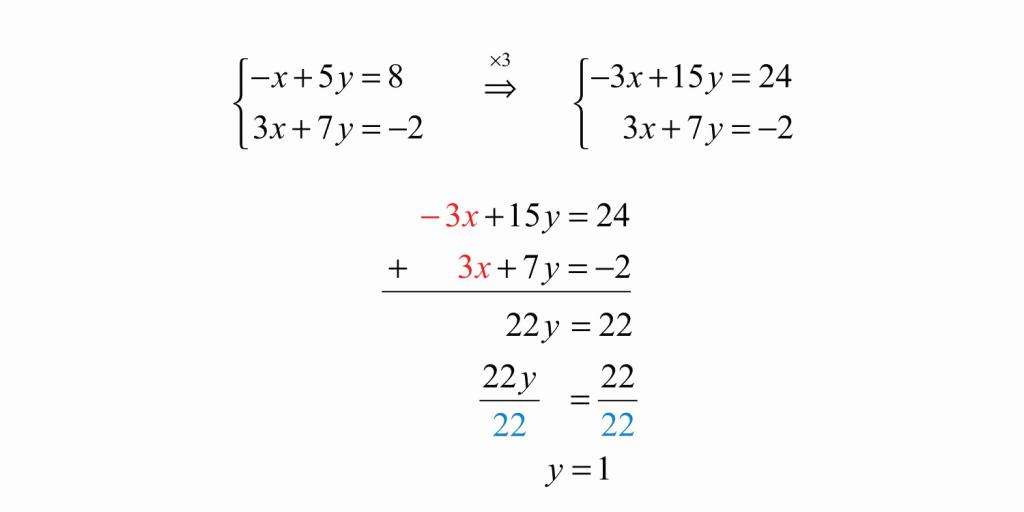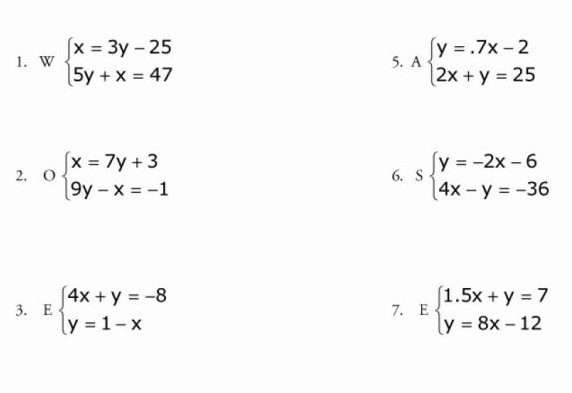Что такое переменная 6 класс
Урок программирования в 6-м классе «Понятие переменной»
Тип урока: Объяснение нового материала.
Организационная форма урока: мини-лекция.
Выдается необходимый минимум теоретического материала (числовые и символьные переменные, формат команды присваивания значения).
Приветствие. Проверка готовности учащихся к уроку, организация внимания. На доске написана тема.
Подготовка учащихся к усвоению нового материала:
На предыдущих уроках мы познакомились с понятием алгоритма и тремя способами его описания. Теперь мы знаем, что описывать алгоритмы можно на естественном языке, на языке схем и на алгоритмическом языке. Но алгоритм, описанный на алгоритмическом языке – это уже программа. А чтобы грамотно писать программы нужно познакомиться с таким понятием как переменная.
Изучение нового материала:
Алгоритмический язык имеет сходство с математическим тем, что в нем также используется понятие величины. Используются в основном, величины двух типов – числовые и символьные, хотя не исключены и другие типы. Числовые величины – это числа: натуральные, целые, вещественные; символьные – буквы, цифры, слова, предложения. В информатике также используется понятие “переменная”. Запишем определение переменной.
Переменная – это объект, которому дано имя и который может принимать различные значения.
Переменные удобно представить в виде “почтовых ящиков” (ячеек памяти компьютера), на которые навешены ярлыки с их именами.
Информация, хранимая в переменной, называется ее значением.
Именем переменной может быть любая буква латинского алфавита.
Переменные, предназначенные для записи числа, называются числовыми. Переменные, в которые можно записывать слова называются символьными.
При этом под словом понимается любой набор символов, которые можно ввести с клавиатуры. Слово, которое помещается в “ящик”, предназначенный для хранения символьной переменной, заключается в кавычки.
Наш “почтовый ящик” имеет некоторые необычные свойства. Когда в него помещается другое значение, начальное стирается и исчезает. Оно уже не может быть восстановлено. Задать значение переменной можно с помощью команды присваивания, которая обозначается знаком “=”.
Что такое переменная 6 класс
Единое национальное тестирование
История Казахстана
Онлайн тесты и шпаргалки по истории Казахстана
Всемирная история
Онлайн тесты и шпаргалки по Всемирной истории.
Математика
Онлайн тесты и шпаргалки по математике.
Химия
Онлайн тесты и шпаргалки по химии.
Физика
Онлайн тесты и шпаргалки по физике.
Биология
Онлайн тесты и шпаргалки по биологии.
География
Онлайн тесты и шпаргалки по географии.
Русский язык
Онлайн тесты и шпаргалки по русскому языку.
Готовые работы
ДИПЛОМНЫЕ РАБОТЫ
КУРСОВЫЕ РАБОТЫ
МАГИСТЕРСКИЕ ДИССЕРТАЦИИ
ОТЧЕТЫ ПО ПРАКТИКЕ
После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт. Этот документ будет подтверждением практической работы студента и основой формирования оценки за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный план и описать свою практическую деятельность.
Мы поможет написать отчёт о прохождении практики с учетом специфики деятельности конкретного предприятия.
Новости сайта
Обучение по государственному образовательному заказу (магистратура)
Комплексное тестирование проводилось с 3 по 7 декабря текущего года. 10 декабря текущего года текущего года начинается прием заявлений для участия в конкурсе по присуждению государственных образовательных грантов на подготовку магистров.
Для участия в конкурсе на присуждение государственного образовательного гранта на подготовку магистров поступающий до 18:00 часов (по местному времени) 14 декабря подает заявление через виртуальную приемную комиссию любой организации высшего и послевузовского образования (далее – ОВПО). Поступающие в магистратуру в заявлении указывают одну группу образовательных программ и до 3-х (трех) ОВПО.
На обучение по государственному образовательному заказу на конкурсной основе зачисляются лица, набравшие наивысшие баллы по КТ и (или) вступительному экзамену и (или) творческих экзаменов: 1) для научно-педагогической магистратуры с казахским или русским языком обучения, в том числе по группам образовательных программ, требующих творческой подготовки, по группам образовательных программ, требующих знания арабского языка – не менее 75 баллов; 2) для профильной магистратуры с английским или с казахским или русским языком обучения – не менее 50 баллов.
Что такое переменные? Переменная величина в математике
Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.
Понятие переменной
Вам будет интересно: Плотность осмия: характеристика, значение, физические и химические свойства, получение и применение
Вам будет интересно: Российская таможенная академия в Москве: описание, адрес, факультеты.
Виды величин
Вам будет интересно: Конспект урока русского языка во 2 классе. Правила «жи – ши», «ча – ща», «чу – щу»
Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
За x2 принимаем некое k, и уравнение приобретает понятный вид:
Вот какую пользу в математику несет введение переменных.
Неравенства, примеры решения
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.
Вам будет интересно: Французские местоимения: типы и виды
Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
Пример с одной переменной:
Делим обе части неравенства на 10 и получаем:
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.
Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
Квадратные неравенства
Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.
Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.
По формуле корней квадратного уравнения получаем:
Или можно было решить это уравнение по теореме Виета:
Методом подбора получаем такие же корни уравнения.
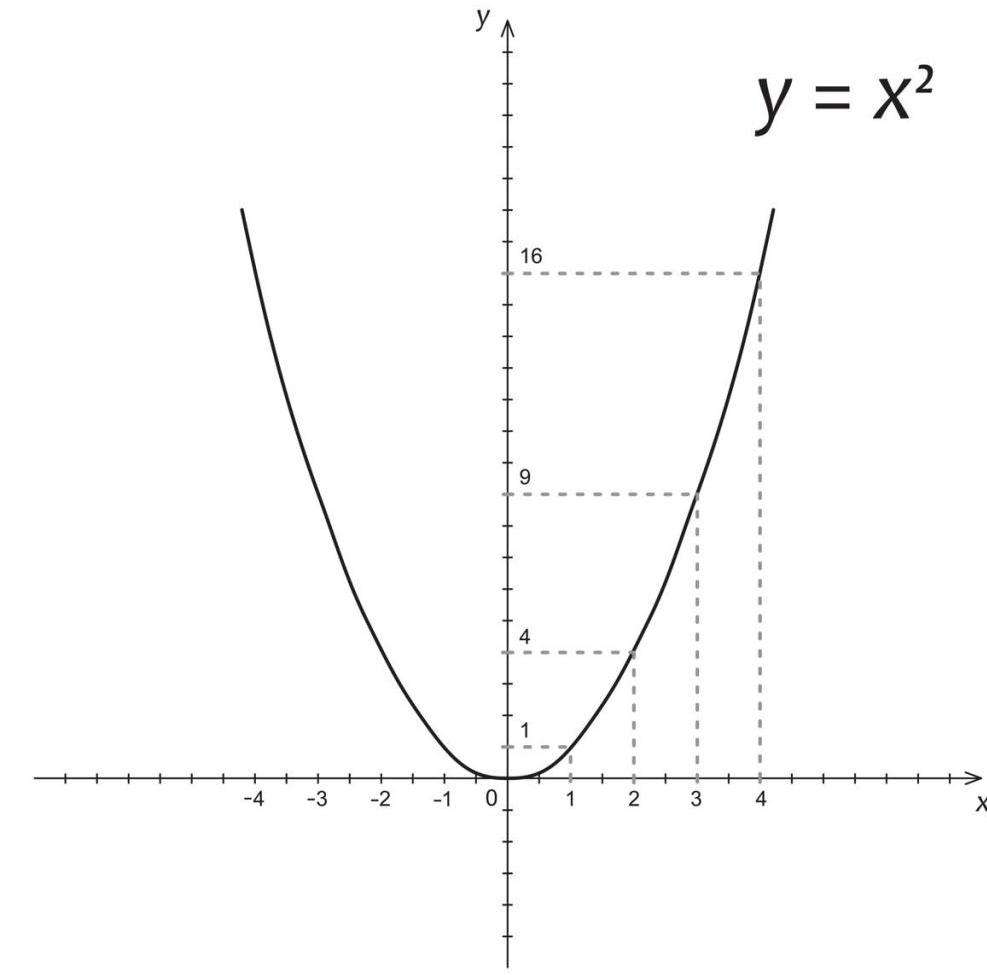
Парабола
1. Определяем, куда направлены ветви параболы.
2. Приравниваем функцию к нулю и находим корни уравнения.
3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.
Выписываем в виде функции:
Приравниваем к нулю.
Дальше решаем как квадратное уравнение и находим нули функции:
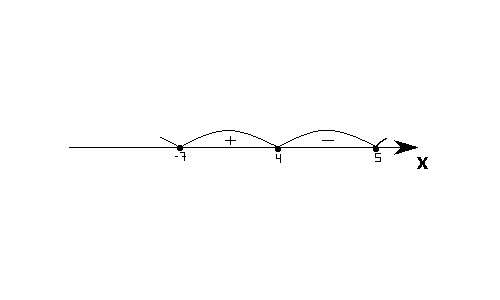
Метод интервалов
1. Находим корни уравнения, при которых неравенство равно нулю.
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.
3. Определяем знак любого интервала.
4. Расставляем знаки у остальных интервалов, меняя их через один.
2) Изображаем их на числовой прямой.
3) Определяем знаки интервалов.
2. Отмечаем их на числовой прямой.
3. Определяем знаки интервалов.
Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.
Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.
Системы уравнений
Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.
Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.
Алгебраический метод
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
Решаем получившееся уравнение и находим икс.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
Метод подстановки
Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:
Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:
Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:
что такое переменная в математике?
Переме́нная — атрибут физической или абстрактной системы, который может изменить свое значение. Примеры переменных: рост ребёнка, температура в воздуха, или параметр функции.
Концепция переменной широко используется в таких областях как математика, естественные науки и техника
В области математики и компьютерных наук, переменные, как правило, обозначаются одним или несколькими словами или символами, такие, как «time» или «x». В математике, новичков часто смущает то, что букву «x» иногда используется для обозначения переменной, как и в выражение y = x2, а иногда и для обозначения неизвестного как в выражении 2x = 6.
При моделировании, переменные необходимо отличать от параметров, несмотря то, что переменная в одном контексте может быть параметром в другом.
В прикладной статистике, переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами
В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать.
[1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.
Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной.
Это множество и задаёт переменную, то есть формально и является ей.
При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.
В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.
В математике переменной может быть как реальная физическая величина, так и некая абстрактная величина, не отражающая процессов реального мира.
В математическом анализе и большинстве смежных разделов математики под переменной x понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества — число называется значением переменной. Само множество называется областью изменения переменной.
Переменная величина
Переме́нная — атрибут физической или абстрактной системы, который может изменять своё значение. Значение может меняться в зависимости от контекста, в котором рассматривается система, или в случае уточнения, о какой конкретно системе идёт речь. Концепция переменной широко используется в таких областях как математика, естественные науки, техника и программирование. Примерами переменных могут служить температура воздуха, параметр функции и многое другое. В широком смысле, переменная характеризуется лишь множеством значений, которые она может принимать.
Содержание
Переменные в математике
В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать. [1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.
Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной. Это множество и задаёт переменную, то есть формально и является ей.
При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.
В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.
Обозначения
Нужно отметить, что аналогичным образом обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах. Например, 
. В этом случае имеются ввиду не переменные, хотя понятия весьма схожи и зависят от контекста.
Суть этого различия между неизвестной и переменной можно пояснить так. Запись можно, с одной стороны, трактовать как утверждение о свойстве неизвестной (в момент высказывания утверждения) величины 
, значение которой можно найти (или уточнить), отталкиваясь от приведенного утверждения как от исходной посылки. В этом случае будет обозначением конкретной, но до проведения выкладок (например, решения уравнения) неизвестной величины. С другой стороны запись можно трактовать как предикат, принимающий значение «истина» при одних значениях, подставляемых на место , и значение «ложь» при других. В этом случае является обозначением места в выражении, на которое могут подставляться различные (переменные) значения с целью определения логического (булева) значения записанного предиката. В этом случае правильнее рассматривать как переменную.
Переменные в программировании
В программировании переменная — это идентификатор, определяющий данные. Обычно это бывает имя, скрывающее за собой область памяти с хранящимися там данными. Переменная может иметь тип, характеризующий множество значений, которые она может принимать. В программировании, переменные, как правило, обозначаются одним или несколькими словами или символами, такими, как «time», «x», «foo» и тому подобное.
Следует отметить, что это значение в некотором смысле схоже с математическим. Математики в XVII веке придумали переменную именно для того, чтобы «забронировать» в формуле место, на которое в нужный момент можно подставить конкретное значение. Бумага в этом процессе является памятью, а обозначения (чаще, буквы) резервируют и именуют области этой памяти. Ощущение неоднозначности возникает из-за того, что формула в математике играет двоякую роль: если это алгоритм вычисления, смысл совпадает с программистским определением; если же формула визуализирует отношения своих элементов, мы абстрагируемся от роли переменной, как ячейки памяти, такое понимание теряет смысл.
Переменные в физике
В физике переменная — это некоторый атрибут модели реального физического процесса, принимающий количественные значения, физическая величина. Множество значений, которые может принимать конкретная переменная, определяется из физических соображений. Физические переменные связываются друг с другом физическими законами, в результате чего получаются математические модели различной степени сложности. Переменные в физике, как правило, кроме количественного значения характеризуются также размерностью.