Что такое переменная origin

Что такое переменная origin

Глава 3. Работа с векторами и матрицами

3.2 Нумерация элементов и определение параметров матрицы

Нумерация элементов матрицы

Элементы матрицы определяются двумя нижними индексами, элементы вектора – одним.

Для ввода нижнего индекса можно щелкнуть в математической панели на кнопке х _n Subscript (Нижний индекс), но лучше использовать клавишу [ (открывающаяся квадратная скобка), так как во время работы с матрицами вводить нижний индекс приходится очень часто.

Чтобы из матрицы выделить вектор (один из столбцов матрицы), используется верхний индекс. Эта операция применяется не очень часто, поэтому для ее выполнения лучше использовать математическую панель инструментов:

– Введите имя матрицы и выделите его синим уголком курсора.

– В математическом меню щелкните на кнопке Matrix and Vector Toolbar (Панель векторов и матриц) и щелкните на кнопке M Matrix Column (Столбец матрицы).

– В появившемся месте ввода пишите номер столбца.

Встроенная переменная ORIGIN

По умолчанию ORIGIN =0, то есть первый элемент вектора, первая строка и первый столбец матрицы имеют индекс ноль.

Чтобы изменить нумерацию индексов в первой строке документа, наберите (прописными буквами) ORIGIN :=1. Можно переопределить встроенную переменную ORIGIN другим способом. Выберите в главном меню команду Tools → Worksheet Options (Инструменты→Параметры документа), в открывшемся окне перейдите на вкладку Built – In Variables → ORIGIN (Встроенные переменные) и в поле Array Origin ( ORIGIN ) введите индекс первого элемента массива (рис.4.2). Переменной ORIGIN можно присваивать разные значения, в том числе отрицательные.

Во всех примерах этой главы установлено значение ORIGIN =1.

Определение параметров матрицы

В MathCAD есть встроенные функции для определения параметров матрицы (рис. 3.4 ):

– rows ( M ) – число строк в массиве или векторе;

– cols ( M ) – число строк в массиве;

– last ( M ) – индекс последнего элемента в векторе;

– max ( M ) и min ( M ) – максимальное и минимальное значения элементов в массиве

– сумма элементов вектора вычисляется нажатием кнопки ∑ V на панели Matrix ;

– tr ( M ) – сумма диагональных элементов квадратной матрицы, называемая следом матрицы, где M – имя матрицы.

число строк в массиве

число столбцов в массиве

индекс последнего элемента в векторе

max и min элементы в массиве

Рис. 3. 4 Функции определения параметров массивов

Источник

Что такое переменная origin

Можно обращаться к отдельным элементам массива, используя нижние индексы. Можно также обращаться к отдельному столбцу массива, используя верхний индекс. Чтобы напечатать нижний индекс, используйте клавишу левой скобки [ и поместите в поле целое число или пару целых чисел. Чтобы вставить оператор верхнего индекса, нажмите [Ctrl]6 и поместите в поле целое число.

Вектор и элементы матрицы обычно нумеруются, начиная с нулевой строки и нулевого столбца. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN.

Нижние индексы и элементы вектора

Рисунок 2 показывает, как это выглядит.

Когда определяются элементы вектора, часть из них можно оставлять неопределенными. Например, если v не был определен, и определяется равным 10, то v0, v1, и v2 все окажутся неопределенными. Mathcad заполняет эти элементы нулями, пока в них не будут внесены необходимые значения. Иллюстрация этого приведена на Рисунке 3. Будьте внимательны: так можно нечаянно создать очень большие векторы и матрицы.

Рисунок 3: Mathcad заполняет нулями все элементы, которые явно не определены.

Нижние индексы и элементы матрицы

Обратите внимание, что нижние индексы, подобно делению и возведению в степень удерживают ввод. Что бы ни печаталось после [, всё остается в нижнем индексе, пока не будет нажат [Space], чтобы выйти оттуда.

Рисунок 4 показывает некоторые примеры того, как определить отдельные элементы матрицы и как просмотреть их. Обратите внимание, что, как и в случае с векторами, Mathcad заполняет неопределенные элементы матрицы нулями.

Можно также определять элементы вектора или матрицы формулой типа v_i :=i, где i — дискретный аргумент. См. следующую главу “Дискретные аргументы”.

Рисунок 4: Определение и просмотр элементов матрицы.

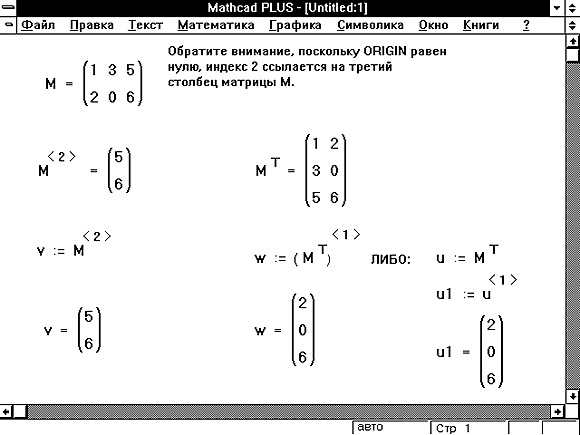
Рисунок 5: Использование оператора верхнего индекса для извлечения столбца из матрицы.

Верхние индексы и столбцы матрицы

Чтобы обратиться ко всему столбцу массива, нажмите [Ctrl]6 и поместите номер столбца в появившееся поле. Рисунок 5 ниже показывает, как присвоить вектору v значение третьего столбца матрицы M.

Можно также извлекать отдельную строку из матрицы, извлекая столбец из транспонированной матрицы. Иллюстрация этого приведена на Рисунке 5.

Изменение значения ORIGIN

По умолчанию массивы Mathcad нумеруются с нулевого элемента. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN. Когда используются нижние индексы, Mathcad учитывает, что массивы нумеруются начиная с принятого значения ORIGIN.

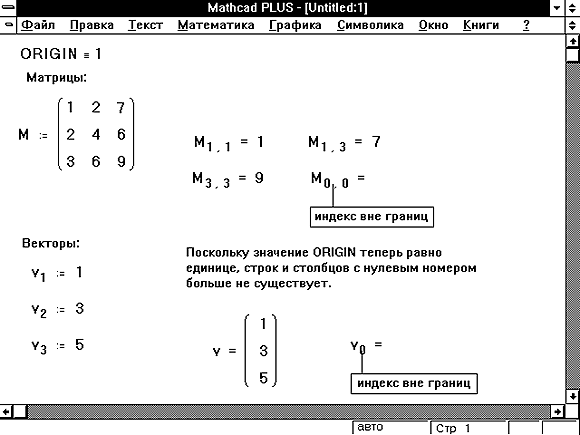
Рисунок 6: Массивы, нумерующиеся с первого элемента вместо нулевого.

Если изменить ORIGIN на 1, Mathcad больше не будет воспринимать нулевой элемент для векторов или нулевые строки и столбцы для матриц. Рисунок 6 показывает рабочий документ с ORIGIN, равным 1. Заметьте, что при попытке обращения к Mathcad теперь сообщает об ошибке “индекс вне границ”.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Что такое переменная origin

РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ. МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

Например, если переменная изменяется в интервале с шагом , то она задается в виде

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

– вектор-столбец; – вектор-строка.

Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

Сначала набирается имя массива и оператор присваивания, например, . Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Источник

Понятие о встроенных функциях Маткада.

Большинство задач в Маткаде решаются с помощью так называемых встроенных функций, т.е. с помощью заранее составленных программ решения той или иной задачи. Каждая такая программа имеет свое имя, по которому она вызывается. Имя можно набирать с клавиатуры, но можно и вызывать с помощью кнопки f(x) главного меню. Нажав эту кнопку, мы вызовем панель Insert Function (вставить функцию), в которой имеется два окна: Function Category (тип функции) и Function Name ( имя функции). Выбрав тип и имя, и нажав кнопку ОК, мы вызовем данную функцию (Рис.1).

Рис.1.Панель вызова функции

Пусть, например, нужно найти синус числа 45. Вызвав панель вставки функции, выберем категорию Trigonometric и название sin, нажмем ОК. На экране появится шаблон со словом sin внутри и скобками. Вставив в скобки число 45, нажмем «=». Получим sin(45)=0.851. Можно было бы набрать левую часть на клавиатуре и, после нажатия знака =, получить тот же ответ.

Аналогично используются и другие встроенные функции Маткада.

В Маткаде массивы могут записываться в виде векторов (одномерные массивы), в виде матриц (двумерные массивы) и в виде таблиц. Мы рассмотрим пока только запись матриц и векторов. Для действий над ними имеется панель Matrix (матрица), показанная на рис. 2.

Рис.2. Панель матриц

Для ввода матриц и векторов нажмем кнопку панели матриц и вызовем этим окно ввода Insetrt Matrix (ввести матрицу), показанное на рис.3.

Рис.3. Окно ввода матриц и векторов. Рис.4. Шаблон вектора.

При вводе вектора в графе columns (столбцы) следует проставить 1, а в графе rows(строки) проставить размер вектора. Появится шаблон, показанный на рис. 4.

Ниже представлено три пятиэлементных массива-вектора: Два из них – численные, третий – буквенный, четвертый состоит из выражений.

При задании буквенных массивов и массивов – выражений необходимо предварительно присваивать им численные значения (за каждой буквой в компьютере должно стоять число). После задания выражений вектора можно, записав его имя и поставив знак =, получить его значение. Рисунок лишний раз иллюстрирует, что Маткад различает строчные и заглавные буквы.

Над векторами определены показанные на рис.5.. операции сложения- вычитания, транспонирования, умножения по математическим правилам умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица).

Порядковый номер элемента, который является его адресом, называется индексом.

Нижняя граница индексации задается значением системной переменной ORIGIN, которая может принимать значение 0 или 1.

Рис.5. Запись векторов в Маткаде.

Имя массива увязано с именами индексированных переменных, значениями которых являются элементы массива. Для этого достаточно в виде подстрочного индекса указать индекс элемента. Например, если третий из представленных массивов имеет имя V, то его элементами при ORIGIN=0 будут индексированные переменные:

Задача 1. Ввести все векторы рис.5 и произвести над ними все действия, проведенные на рисунке. Матрицы в Маткаде вводятся так же, как и векторы, но число столбцов в них – больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рис.6 показаны различные способы ввода матриц.

Задача 2.Ввести все матрицы, приведенные на рис.6.

Рис.7. Роль переменной ORIGIN

В Маткаде определены следующие действия над векторами и матрицами:

А) сложение – вычитание,

В) скалярное и векторное умножение,

Ж) выделение столбцов.

Они выполняются с использованием следующих кнопок панели Matrix:

кнопка индексации элементов матрицы,

кнопка обращения матрицы,

кнопка скалярного произведения векторов и матриц

кнопка транспонирования матрицы,

кнопка векторного произведения двух векторов

кнопка сложения векторов

кнопка выделения столбца матрицы

кнопка вычисления детерминанта матрицы.

На рис.8 приведены все эти действия над матрицами, приведенными на рис.6.

Задача.3: Произвести над матрицами все действия, показанные на рис.8..

Рис.8. Действия над матрицами

Задача.4: Ввести две произвольные матрицы. Перемножить. Например:

Проверьте на бумаге правильность произведенных выше действий

Рис.9. Пример выполнения задачи 4

Обращение и вычисление определителя возможно только для квадратных матриц.

Задача 5.. Введите произвольную квадратную матрицу, найдите обратную ей и вычислите определитель, используя показанные выше кнопки встроенных операторов.

Рис.10. Пример выполнения задачи 5..

Как известно, умножение матрицы на обратную дает единичную матрицу. Проверим, правильно ли было проведено обращение

Задача 6. Найти скалярное и векторное произведения двух заданных трехэлементных векторов: Проверить на бумаге правильность вычислений.

Рис.11.Пример выполнения задачи 6..

При рассмотрении матриц больших размеров удобно выделять их столбцы. Мы будем использовать его в модулях 2 и 3 при решении сложных задач.

Задача 7. Используя кнопку выделения столбцов, выделите столбцы произвольной матрицы, например:

Рис.12.Пример выполнения задачи 7.

В Маткаде имеется большое количество встроенных функций для действий над матрицами и векторами. Рассмотрим некоторые из них.

Вычисление максимального и минимального элементов матрицы или вектора производится с помощью встроенных функций Max(A )и Min(A).

Задача 8. Вычислить максимальный и минимальный элемент произвольной матрицы, например:

Рис13. Вычисление максимального и минимального элемента матрицы.

Определение количества столбцов и строк в матрице удобно для проверки действий над многомерными матрицами и векторами. Оно производится с помощью встроенных функций Cols(A)- число столбцов матрицы А и Rows(A)-Число строк матрицы А

Задача 9. Определить число строк и столбцов в произвольной матрице, например

Рис.13. Пример выполнения задачи 9.

Рис.14. Формирование единичной матрицы и вычисление следа матрицы.

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник