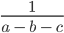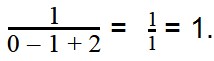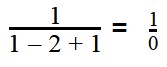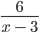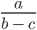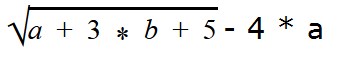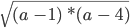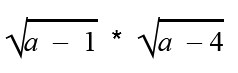Что такое переменная в алгебре 8 класс примеры

Что означает переменная в математике?

Тем не менее, каково количество членов в алгебраическом выражении?

Каждое выражение состоит из терминов. Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные. Каждый член в алгебраическом выражении отделяется знаком + или J. Условия: 5x, 3y и 8. … В члене 5x коэффициент равен 5.

далее, какие 3 типа переменных?

тогда, что такое переменный пример?

Сколько терминов в выражении?

Как найти термины в последовательности?

Какие 5 переменных?

Как вы объясняете переменные студентам?

Какая переменная должна оставаться постоянной?

Переменная в эксперименте, которая поддерживается постоянной для оценки взаимосвязи между несколькими переменными, является управляющая переменная.

Какие бывают 5 типа переменных?

Какие бывают 4 типа переменных?

Четыре типа переменных

Как видите, существует четыре различных типа шкал измерения (номинальный, порядковый, интервальный и коэффициент). Каждая из четырех шкал, соответственно, обычно предоставляет больше информации об измеряемых переменных, чем предыдущие.

Что такое переменная в 2х?

Какие термины используются в выражении?

Срок: каждое выражение состоит из терминов. Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные. Фактор: что-то, что умножается на что-то еще. Фактор может быть числом, переменной, термином или более длинным выражением.

Как называется термин без переменной в алгебраическом выражении?

Что означает 3x в математике?

3x это коэффициент с переменной x. Например: 3x + 4. X3 должно означать x с показателем 3.

Что такое формула ряда?

Серия последовательности сумма последовательности к определенному количеству членов. Его часто пишут как S_n. Итак, если последовательность 2, 4, 6, 8, 10,…, сумма до 3 членов = S₃ = 2 + 4 + 6 = 12.

Как найти следующие четыре члена последовательности?

Переменная называется непрерывной, если она может принимать бесконечное количество действительных значений. Примеры непрерывная переменная расстояние, возраст и температура.

Сколько существует типов переменных?

Существуют

три типа

категориальных переменных: двоичных, номинальных и порядковых переменных.

Как объяснить, что такое переменная?

Что делают переменные при кодировании?

Какая ключевая переменная?

A общая переменная между двумя наборами данных, которые, следовательно, могут использоваться для связывания записей между ними. Ключевая переменная может быть формальным идентификатором или квазиидентификатором.

Что такое пример постоянной переменной?

TL; DR: В научном эксперименте контролируемая или постоянная переменная переменная, которая не меняется. Например, в эксперименте по проверке воздействия различных источников света на растения необходимо, чтобы другие факторы, влияющие на рост и здоровье растений, такие как качество почвы и полив, оставались постоянными.

Как вы контролируете переменную в статистике?

Переменные могут быть контролируются напрямую, поддерживая их постоянными на протяжении всего исследования (например, контролируя комнатную температуру в эксперименте), или ими можно управлять косвенно с помощью таких методов, как рандомизация или статистический контроль (например, для учета характеристик участников, таких как возраст, в статистических тестах).

Как узнать, постоянна ли переменная?

число перед алфавитом (переменная) называется константой. Переменная: символ, который принимает различные числовые значения, называется переменной. Алфавит после числа (константы) называется переменной.

Источник

Что такое переменная? Буквенные обозначения переменных

Содержание

Зачем нужны буквы в математике? Почему в математике помимо цифр используют еще и буквы? Почему бы не оперировать просто цифрами? Давайте попробуем найти ответы на эти вопросы.

А потому что буквы нам нужны для обозначения переменных. Предположим, у нас есть выражение:

Что такое «x»?

Мы могли этот же пример записать так:

почерк плюс три равно десяти

Или так: знак вопроса плюс три равно десяти

На самом деле непринципиально, как мы обозначим переменную. Мы можем поставить вместо нее вот такой смайлик — 😀

Тогда это будет смайлик плюс три равно десяти

Мы можем решить это уравнение и найти значение, которое соответствует этому смайлику.

Если бы вместо смайлика было записано какое-то число, то это уже не была бы переменная.

Вот такая первая причина использования букв. Еще буквы используют для выражения отношения между числами в тех или иных выражениях.

Например, если в записи

Если есть два числа, одно из которых больше другого, то с помощью букв это можно записать вот так:

Буквы в математике – это всего лишь символы, и ничего более. И использовать можно абсолютно любую букву латинского алфавита, которая больше всего нравится.

При решении задач можно использовать и письменный, и печатный вариант написания буквы. Для обозначения чисел чаще всего используют маленькие прописные буквы.

Источник

Числовые, буквенные выражения и выражения с переменными: определения, примеры

В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.

Числовые выражения

Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.

Учитывая все сказанное, дадим определение. Что такое числовое выражение?

Определение. Числовое выражение

Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.

Поясним данное определение.

Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:

деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.

Скобки в числовых выражениях

Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:

В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.

Буквенные выражения

После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.

Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.

Определение. Буквенное выражение

Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.

Приведем пример сложного буквенного выражения.

Выражения с переменными

В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.

Определение. Выражения с переменными

Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.

Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.

Источник

что такое переменная в математике?

Переме́нная — атрибут физической или абстрактной системы, который может изменить свое значение. Примеры переменных: рост ребёнка, температура в воздуха, или параметр функции.

Концепция переменной широко используется в таких областях как математика, естественные науки и техника

В области математики и компьютерных наук, переменные, как правило, обозначаются одним или несколькими словами или символами, такие, как «time» или «x». В математике, новичков часто смущает то, что букву «x» иногда используется для обозначения переменной, как и в выражение y = x2, а иногда и для обозначения неизвестного как в выражении 2x = 6.

При моделировании, переменные необходимо отличать от параметров, несмотря то, что переменная в одном контексте может быть параметром в другом.

В прикладной статистике, переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами

В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать.

[1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.
Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной.

Это множество и задаёт переменную, то есть формально и является ей.
При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

В математике переменной может быть как реальная физическая величина, так и некая абстрактная величина, не отражающая процессов реального мира.

В математическом анализе и большинстве смежных разделов математики под переменной x понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества — число называется значением переменной. Само множество называется областью изменения переменной.

Источник

Область допустимых значений функции

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 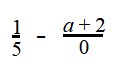— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

Рассмотрим каждый случай в отдельности.

Пример 7

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Источник